飞行器级间段跨声速脉动压力特性试验
武利龙,操小龙,王靖,周丹杰,罗金玲
1.北京机电工程研究所,北京 100074 2.北京空天技术研究所,北京 100074
锥柱外形作为航天类飞行器的一种常用外形,在跨声速飞行时由于级间锥柱段的膨胀加速会在连接舱后的肩部区域达到局部超声速产生激波,进而产生较强的压力脉动,该压力直接作用在飞行器表面会导致局部大载荷、诱导抖振响应进而导致结构破坏,从而大大缩短飞行器使用寿命;此外,脉动压力还会造成严重的气动噪声,影响飞行器内部仪器正常工作。因此,开展锥柱外形飞行器的跨声速脉动压力特性研究对工程设计十分必要。
国内外对于此类飞行器外表面脉动压力的研究始于20世纪60年代,Robertson[1]最早通过风洞试验研究给出了锥柱体外形飞行器的静态和动态压力分布,揭示了产生动态压力的非稳态流动机理。徐立功和刘振寰[2]分析了机动再入飞行器表面脉动压力环境,并根据高超声速无黏流计算的表面压力分布,给出了一套预测脉动压力环境统计特性的工程计算公式。Lananelli和Wolfer[3]给出了一套脉动压力和功率谱的预测方法,适用于零压梯度附体流和光滑、粗糙壁面上分离湍流边界层流动。黄岬嵋和王剑[4]描述了飞机加改装部件绕流的典型流态及脉动压力。孟德虹等[5]通过数值模拟方法研究了某型战斗机垂尾的脉动压力特性。陈伟芳等[6]基于超声速和高超声速流动再入体表面的压力分布给出了一套预测表面脉动压力分布的工程方法,研究了马赫数Ma、迎角、壁面温度等因素对再入体表面脉动压力环境的影响。Kumar等[7]通过试验研究了火箭等锥柱外形跨声速飞行时尾锥处的脉动压力,分析了不同的尾锥角度和内外径比对脉动压力的影响规律。龙万花等[8]利用平均流场的数值模拟与基于实验的工程预测相结合的方法对跨声速下旋成体的表面脉动压力环境进行了分析预测,给出了旋成体在不同迎角、不同Ma条件下表面脉动压力系数和功率谱分布。洪杰等[9]通过CFX软件分析了超声速和高超声速球头锥-柱再入飞行器表面脉动压力分布特性,给出了一套预测表面稳定压力和脉动压力环境的工程方法。王娜和高超[10]通过对弹体模型进行表面脉动压力特性实验研究,给出了在跨声速、超声速不同迎角条件下沿弹轴测点的脉动压力系数、频谱曲线以及相关性系数。操小龙等[11]通过风洞试验研究对锥柱外形飞行器亚、跨、超声速条件下的脉动压力特性进行了分析,给出了脉动压力系数和功率谱密度随Ma和迎角的变化规律。任淑杰等[12]通过采用雷诺平均Navier-Stokes方程求解流场、非线性噪声求解方程求解声场相结合的技术途径,给出了一种预示大型火箭结构脉动压力环境的方法。此外,美国NASA兰利研究中心等机构的研究人员[13-17]近年来针对火箭等锥柱外形飞行器的跨声速脉动压力环境开展了大量的地面试验以及飞行试验测量,并对两者进行了对比分析。
通过上述国内外关于锥柱外形脉动压力的研究可以看出,锥柱外形参数是影响局部脉动压力量级的重要因素之一,然而关于不同锥角和锥长大小对脉动压力影响规律的研究报道较少,同时,受制于早期传感器尺寸以及频响范围的约束,相关试验测量值相对较小。因此,本文通过试验研究,开展锥角和锥长对锥柱外形飞行器跨声速脉动压力的影响规律研究,为航天类飞行器结构设计提供较好的支撑。
1 试验模型及设备
本文研究的锥柱外形示意图如图1所示,试验共选取了5种不同锥角模型,分别为10°、12.7°、15.3°、20°和25°。测点从肩部膨胀拐点后开始沿上母线依次布置,具体位置及编号如图1所示。
为了分析锥长对脉动压力的影响,固定锥角,本文选取了锥角θ=12.7°为研究基准,取原始缩比模型的锥长为l0,共选取了5种不同锥长l尺寸模型,其长度分别为l/l0=0.48、0.62、0.82、1.0、1.27,具体如图2所示,其中li为第i种锥形舱段模型的长度,di为与第i种锥形舱段模型连接圆柱段的直径。
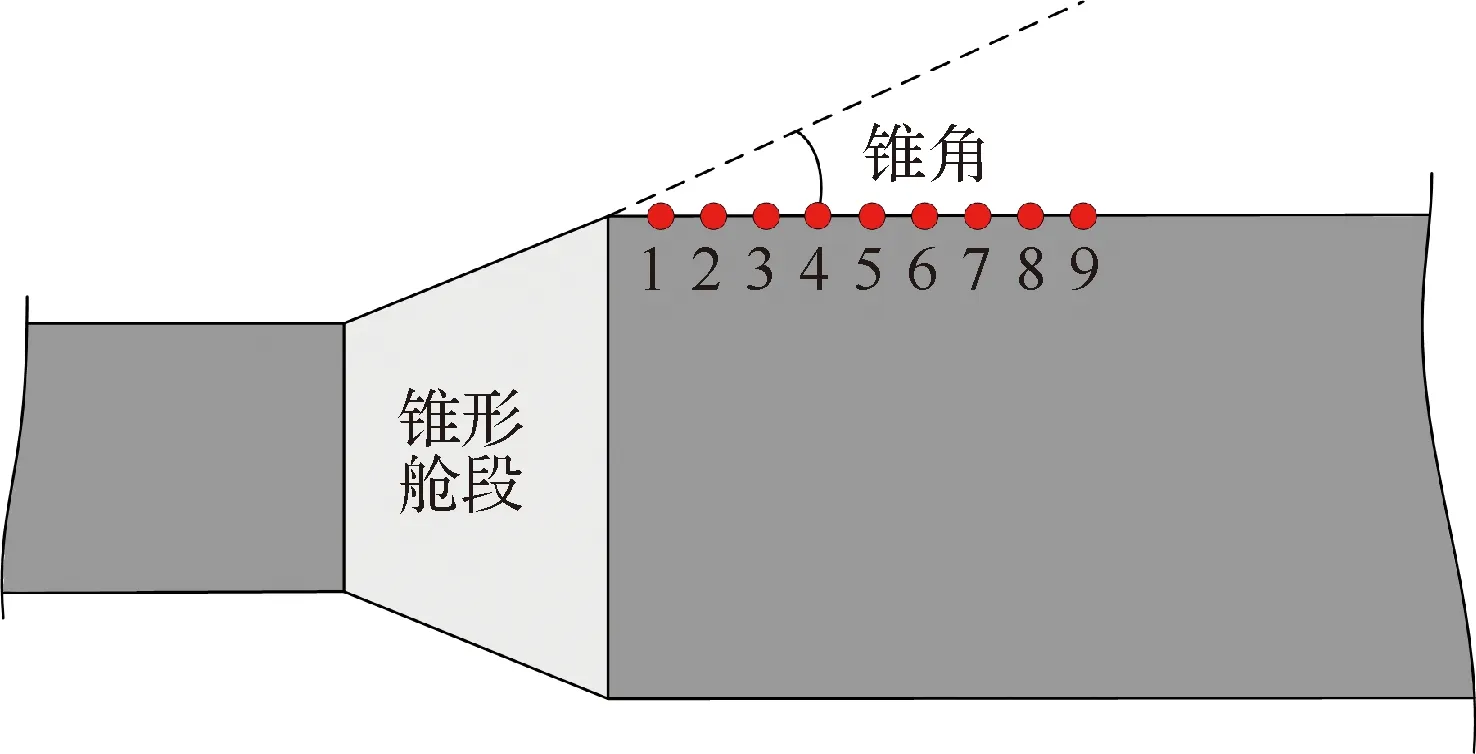
图1 锥柱外形及测点位置Fig.1 Cone-cylinder configuration and position of measurement points
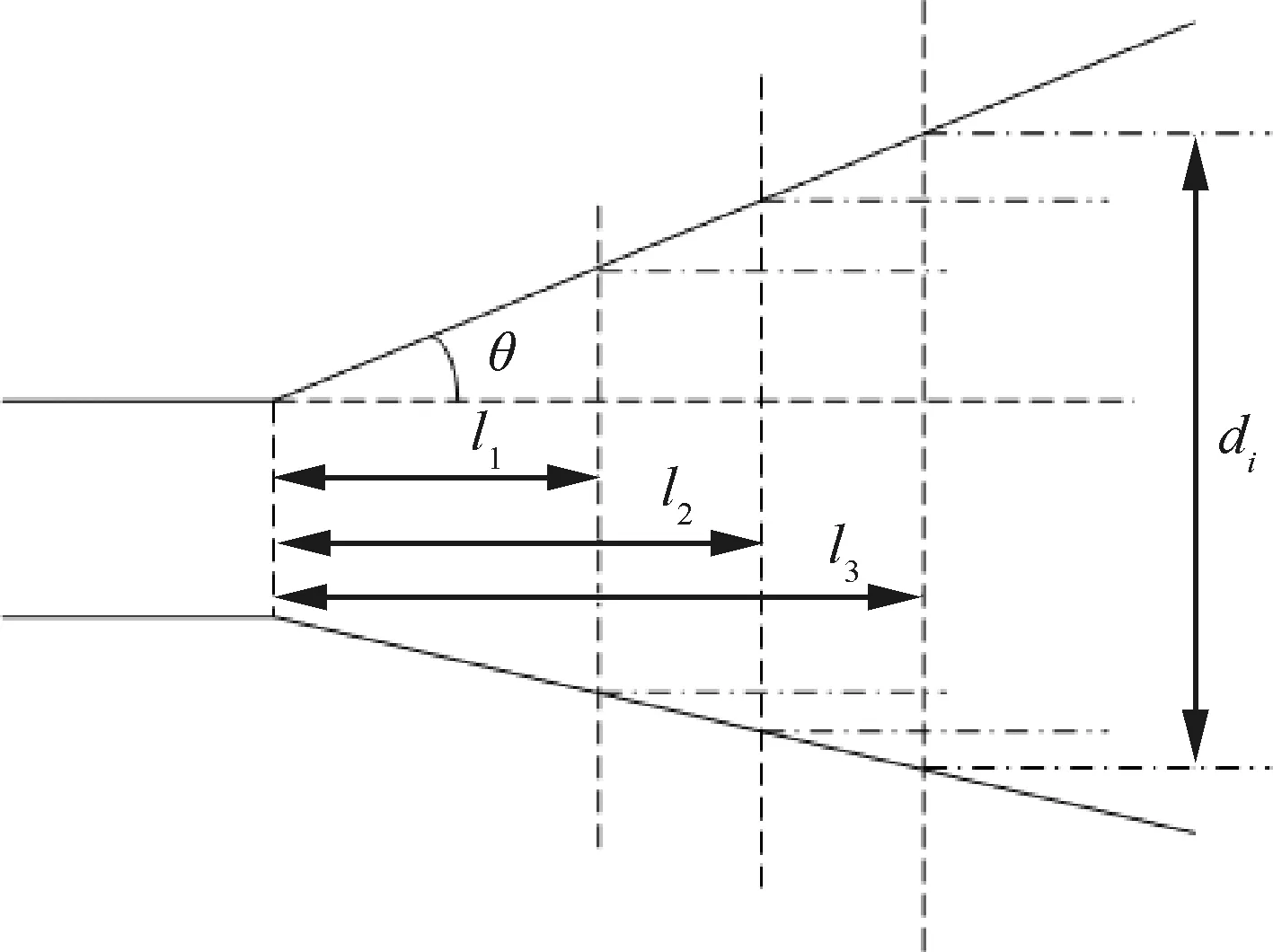
图2 模型锥长变化示意图Fig.2 Schematic diagram of models with different cone length
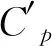
(1)
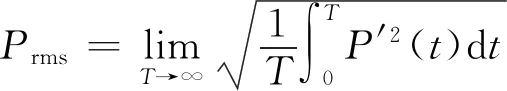
(2)
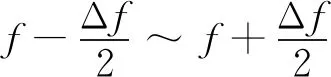
2 试验结果及分析
各个锥角模型的试验马赫数范围均为0.75~1.2,迎角均为0°。由于脉动压力峰值对于自由来流马赫数比较敏感,所以试验测量马赫数间隔取为0.01。
2.1 流动规律
对于如图1所示的锥柱外形,当跨声速气流流过时,由于锥柱连接舱前端压缩角和后端膨胀角的二次加速,锥柱体肩部后局部区域气体流速会达到超声速,在肩部后产生明显的激波。试验纹影如图3所示,随着Ma增大,肩部的激波影响区域逐渐加大,并沿着轴向向后推移,在肩部区域形成了明显的斜激波和正激波,呈现出λ形,并且该激波表现出不稳定特性,在肩部区域出现明显的振荡现象。此外,对于较大锥角情形由于物面外折在肩部区域还会伴随有流动分离,分离后再附区域会形成再压缩激波,激波与边界层干扰会进一步诱导流动分离。正是由于局部激波、流动分离以及边界层等复杂流动的相互干扰在肩部区域产生了强烈的脉动压力现象,试验的所有模型,随着来流Ma的增加均在肩部出现了上述的激波及振荡现象,并表现出了较强的脉动压力,但不同级间段模型量值上出现了较大的差异。

图3 跨声速肩部区域流动纹影图片Fig.3 Schlieren flow-visualization pictures on shoulder region at transonic speed
2.2 不同锥角结果
对5种不同锥角模型肩部测点数据进行处理分析,沿上母线各个测点处脉动压力系数随Ma的变化规律,如图4所示,其中各个测点的脉动压力系数均采用最大峰值进行了归一化,后述结果处理方式相同。可以看出,5个锥角模型的脉动压力系数峰值均出现在肩部区域的前4个测点位置,其中距离肩部0.05d和0.15d(d为锥形舱段后端圆柱的直径)的1和2号位置处最为严酷。结合流动纹影以及图5所示最大和最小锥角模型在测点1处的功率谱密度(PSD)分布可以得出,严酷的脉动压力主要是由于肩部不稳定的激波振荡所致,并且从图中可以看出在频率f=100 Hz左右出现了明显的以低频为主导的能量集中区域。此外,通过分析各个测点峰值及对应的Ma可以看出,肩部的激波随着Ma的增加在不断后移,并且激波的强度在不断减弱,在距离肩部0.35d的4号测点处其脉动压力系数已降至最大峰值的50%左右,继续向后会进一步减小。
提取不同锥角模型肩部1、2号测点的脉动压力系数峰值随Ma的变化结果,具体对比如图6所示,可以看出,1号测点的脉动压力峰值主要集中在Ma=0.81~0.86范围内,而2号测点主要集中在Ma=0.87~0.92之间。对于各测点的脉动压力峰值仅在很窄的Ma区间内出现,随着激波的推移会迅速减小。将各个锥角模型的脉动压力系数最大值进行对比分析,结果如图7所示,可以看出随着锥角增加脉动压力系数先表现出平缓增加,当锥角大于15°时,Cp′增加幅度进一步加大,锥角从10°变化至25°脉动压力系数峰值增大了将近一倍。
2.3 不同锥长结果
对于不同锥长模型,沿上母线分别选取肩部前4个测点,即测点1、2、3和4,分析锥长对脉动压力的影响规律。图8为上述4个监测点处的脉动压力系数随着锥长和Ma的变化结果。从图8(a)测点1处结果中可以看出,锥长比l/l0为1.27的模型首先在Ma=0.809处达到峰值,随着锥长的减小,各个模型达到峰值的Ma在增大,对于l/l0=0.48的模型在Ma=0.903处才达到峰值,并且各个模型的Cp′峰值结果比较接近。对于图8(b)测点2结果,同样可以看出随着锥长的减小,各个模型达到峰值的Ma在增大,但最短的l/l0=0.48模型的峰值明显小于其他4种情形,即沿流向从测点1到测点2锥长最小模型的脉动压力系数峰值首先出现了较大幅度的减小。结合该模型在测点1处Cp′峰值出现的Ma最大,说明锥长最短的模型仅在很窄的Ma区间出现脉动压力峰值,并且在肩部的作用区域很小。
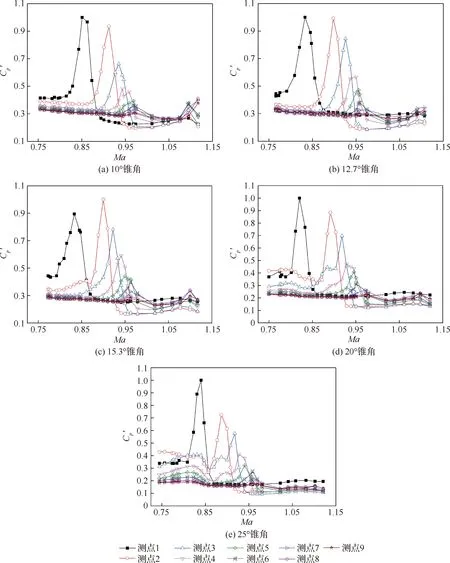
图4 5种锥角模型肩部区域脉动压力系数随马赫数的变化Fig.4 Variation of fluctuating pressure coefficient with Mach number for five cone angle configurations
进一步对测点3、4进行分析,结果分别如图8(c)和图8(d)所示。从测点3的结果可以看出,锥长比l/l0=0.62的模型Cp′峰值出现了大幅减小,为最长模型的55%;同时l/l0=0.82模型也出现了一定幅度的减小,其峰值为最长模型峰值的78%。对于图8(d)所示的测点4结果,可以看出l/l0=0.48,0.62,0.82,1.0,这4个模型的Cp′峰值均出现了进一步的骤减,其中前3个较短模型的峰值分别为最长模型的48%、53%和58%,而次长模型也仅为最长模型峰值的69%。

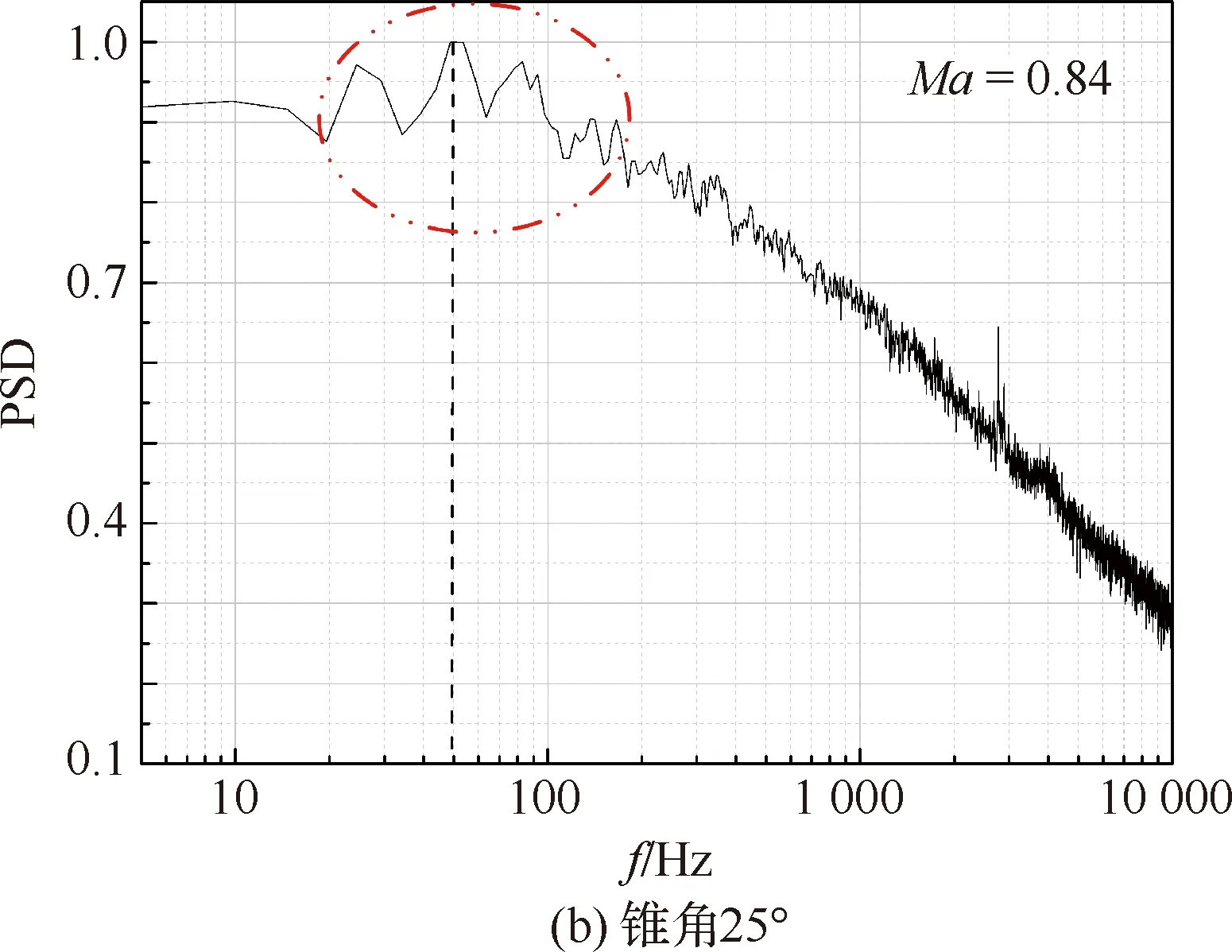
图5 两种锥角模型测点1处的功率谱密度分布Fig.5 Power spectral density of two cone angle configurations at Point 1
通过上述结果分析可以看出,随着锥柱连接段越长,上母线肩部区域的脉动压力作用范围越大,同时在该作用区域脉动压力峰值维持的Ma区间也越宽;该结果进一步表明锥柱级间段越长,气流加速越大、激波也越强,当其缩短到一定长度时,肩部区域的脉动压力峰值基本消失。
选取最短和最长两个模型肩部测点1做功率谱密度分析,结果如图9所示,可以看出在频率为100 Hz以内的窄带区间同样出现了较为明显的能量集中区域,说明肩部脉动压力峰值同样为低频的不稳定激波振荡所致。
此外,对比5种不同锥长模型的脉动压力系数最大值可以发现,结果量值接近,具体如图10所示,从而可以说明锥长对脉动压力局部峰值的大小几乎没有影响,影响的只是Cp′峰值出现的敏感Ma大小以及肩部区域作用的范围大小。
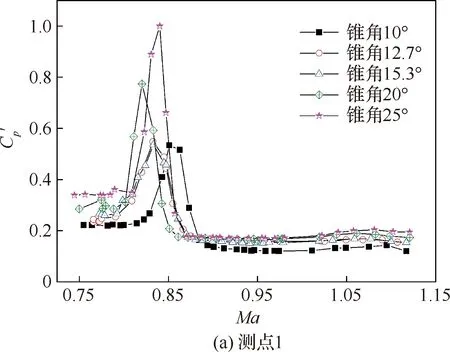
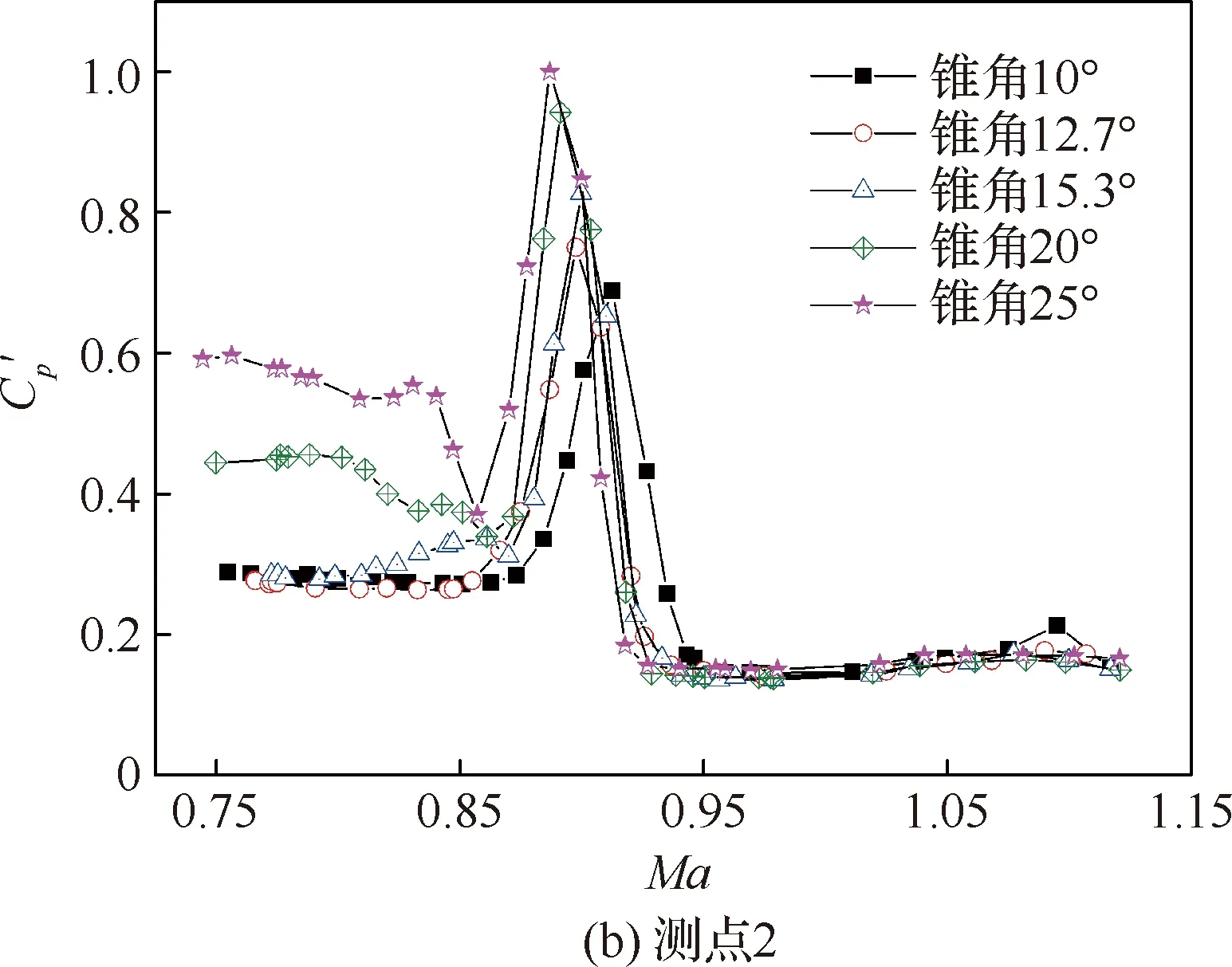
图6 测点1、2处Cp′随锥角和Ma的变化Fig.6 Variation of Cp′ with cone angle and Ma at Point 1 and Point 2
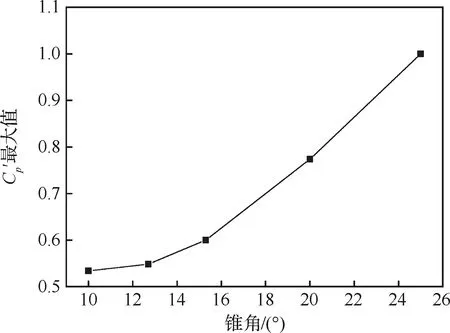
图7 脉动压力系数最大值随锥角的变化规律Fig.7 Variation of the maximum of fluctuating pressure coefficient with cone angle
3 结 论
本文通过脉动压力风洞试验测量的方法,对比分析了不同锥角和锥长大小对锥柱外形飞行器跨声速(Ma=0.75~1.2)脉动压力的影响规律,结论如下:

图8 不同测点Cp′随锥长比和Ma的变化规律Fig.8 Variation of Cp′ with cone length ratio and Mach number at different measuring points

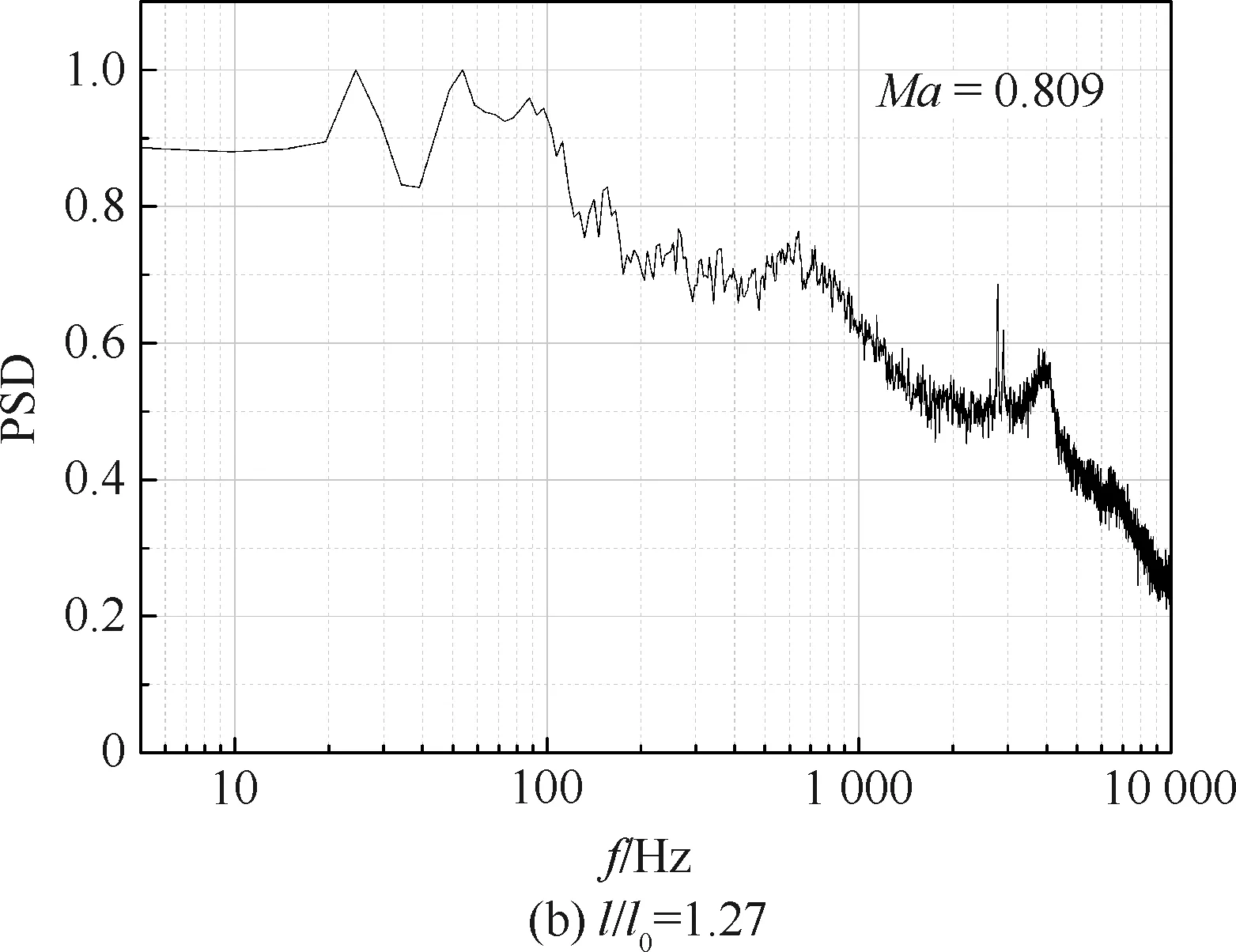
图9 两种不同锥长模型测点1处的功率谱密度分布Fig.9 Power spectral density of two cone length configurations at Point 1
1)对于级间段为锥柱外形设计的飞行器,在跨声速飞行时肩部区域会出现较强的脉动压力。
2)对比分析5种不同的锥角模型,锥角大小分别为10°、12.7°、15.3°、20°和25°,肩部区域的脉动压力峰值均呈现随Ma增加先增大后减小的趋势,并且峰值仅在很窄的Ma区间内出现,随着肩部激波的后移会迅速减小;此外,所有模型的跨声速脉动压力峰值均作用在肩部拐点后1.0d的范围内,其中较为严酷区域位于0.35d的区域范围,且最大峰值随着锥角的增加表现出,当其小于15°时先平缓增加,随着锥角进一步增大,Cp′增加幅度进一步加大。

图10 脉动压力系数最大值随锥长比的变化规律Fig.10 Variation of maximum Cp′ with cone length ratio
3)对于相同锥角、不同锥长的模型,级间段越长,脉动压力在肩部区域的作用范围会越大,同时在该作用区域脉动压力峰值维持的Ma区间也会越宽;对比5种不同锥长模型的脉动压力系数最大值,可以看出其结果接近,进一步表明影响最大值的关键参数为锥角大小。
4)对峰值点脉动压力的功率谱密度分析结果表明,以低频为主导的窄带区间能量较为突出,其主要集中在100 Hz左右,进一步表明严酷的脉动压力主要是由于肩部不稳定的激波振荡所致。
综合整个试验结果,其规律性较好,对于飞行器设计具有重要的支撑作用。

