结合离线知识的时变结构模态参数在线辨识

岳振江，刘莉,2,*，余磊，康杰

1.北京理工大学 宇航学院，北京 100081 2.北京理工大学 飞行器动力学与控制教育部重点实验室，北京 100081

随着对飞行器性能要求的不断提高，飞行器结构的动力学特性的时变问题日益显著。在线获取结构模态参数对飞行器加工制造[1]、飞行过程中的热结构[2]、气动弹性控制[3]、管路振动失稳[4]以及结构健康监测[5]等问题十分重要。飞行器结构的时变特征常出现在飞行过程中，其结构所受激励难以准确测量，因此采用仅输出模态分析方法成为解决此类时变结构辨识问题的有效手段。

时变结构模态参数在线辨识方法一般为时域参数化方法，主要有基于时变状态空间(Time-dependent State Space，TSS)模型和时变时间序列(Time-dependent Time Series，TTS)模型两类参数化模型[6]。Houtzager等[7]提出了一种基于预测器的递推子空间辨识方法，只需通过最小二乘求解线性问题即可获得辨识结果，并通过二元翼段的颤振辨识问题进行验证。倪智宇等[8]引入仿射投影方法对状态量进行递推求解，进一步减少了计算量，并应用于带有大型挠性附件的卫星模态参数在轨辨识。Basseville等[9]为有效处理湍流这一具有明显非平稳特征的激励，通基于协方差的随机子空间方法对飞行状态下的飞行结构模态参数进行了辨识。Avenda等[10]在随机结构化方法基础上提出了一种广义随机约束的时间相关自回归滑动平均(Time-dependent Auto-Regressive Moving Average,TARMA)模型，采用最大后验概率构建费用函数，并应用于风车结构的模态参数辨识。Ma等[11]通过将TARMA模型参数在核空间展开获得核化TARMA模型，在降低计算量的同时保证了低信噪比情况下的辨识精度。

神经网络(Artificial Neural Network,ANN)在结构参数辨识中获得广泛应用，但主要集中在时不变结构辨识问题中。一类工作为通过ANN直接从原始数据中提取结构参数。Liu等[12]针对各向异性的复合层板的材料弹性参数辨识问题，根据结构振动位移通过ANN进行辨识。Xu等[13]选择一个已知的近似参考结构通过计算二者响应的偏差，对结构的刚度和阻尼进行估计。Facchini等[14]针对结构安全评价问题，首先根据结构振动响应的谱张量定义4个频率相关的指标，对原始数据进行抽象，采用ANN建立指标与结构频率之间的映射关系，获得结构当前频率。另一类工作为通过ANN与结构的参数化模型相对应，进而获得结构相关参数。Fei等[15]在激励已知的情况下，根据待辨识系统的传递矩阵信息构建线性神经网络框架(不使用非线性激活函数)，根据系统所受激励和响应获得结构传递矩阵。Tutunji[16]针对使用非线性激活函数的神经网络通过Taylor展开进行线性化，进而建立网络模型与结构传递函数之间的关系。许斌等[17]通过ANN与自回归滑动平均(Auto-Regressive and Moving Average,ARMA)模型的等效性，提出一种从ANN模型得到ARMA模型参数，进而可以获得结构参数的方法。在时变结构辨识方面，于开平等[18]采用全连接网络框架，通过递推最小二乘建立时序关系，实现模态参数在线辨识，并讨论了跟踪能力与计算代价之间的权衡。

深度学习在过去十年发展迅速，在众多领域取得显著成果[19-20]。循环神经网络(Recurrent Neural Network,RNN)及其重要改进—长短时记忆网络(Long Short-Term Memory,LSTM)，作为其中一类重要的模型可以有效提取序列上下文信息，建立时序关系，处理序列相关问题，在自然语言处理等[21-23]方面获取重要突破。

本文采用LSTM网络建立时变结构的在线模态参数辨识网络模型，通过在离线条件下引入结构的先验信息，以及LSTM内在的脉冲噪声鲁棒性，缓解在线条件下虚假辨识结果问题、对实际环境下脉冲噪声不鲁棒的问题，实现时变结构模态参数高效、可靠的在线辨识，并通过移动质量梁实验系统进行验证。

1 时变结构模态参数在线辨识任务

1.1 传统参数化模型

对于一般线性时变结构，其动力学方程为

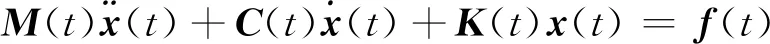
(1)

式中：M(t)、C(t)和K(t)分别为结构的时变质量矩阵、阻尼矩阵和刚度矩阵；x(t)和f(t)分别为结构的位移响应和外力。

与描述平稳过程的ARMA模型相比，TARMA模型中AR与MA部分的系数矩阵为时变矩阵，采用TARMA模型对非平稳响应信号序列建模可表示为[24]

(2)

对TARMA模型中待估参数Ai和Ci时变演化过程进行非结构化的、随机结构化的或是确定性结构化的建模描述，根据已有非平稳振动响应序列，对其进行估计。

(3)

在获得TARMA模型的估计参数后，在每一时刻，根据AR部分的系数矩阵通过求解一个广义特征值问题获得系统特征根[25]

(D-λrI)Vr=0

(4)

式中：λr为特征根；Vr为特征向量；系统特征矩阵D∈Rnana×nana，

(5)

对于线性慢时变结构，其特征根都是近似复共轭的[26]。结构模态频率为

(6)

式中：Ts表示采样间隔；·*表示复共轭。

由上述时域参数化辨识过程可知，时域参数化辨识方法首先根据响应信号序列x[t],x[t-1],x[t-2]…建立原系统的等效TARMA模型，计算TARMA模型的特征参数获得原系统的模态参数。在线辨识首要解决的问题是如何确定TARMA模型阶数。较低的模型阶数无法有效反映系统特性，较高的模型阶数会导致辨识结果存在虚假模态，需要进行筛选，二者均对在线应用构成挑战。此外由于TARMA模型参数是通过基于高斯分布假设的最小二乘类估计方法获得，难以有效应对结构实际服役环境中广泛存在的脉冲噪声。因此面向工程应用的时变结构模态参数在线辨识必须有效解决这些问题。

1.2 循环神经网络模型

循环神经网络(RNN)是一类引入反馈机制实现处理序列数据的神经网络[27]。针对一组响应信号序列x[t],x[t-1],x[t-2]…，RNN每层结构如图1所示，隐层输出h反馈到输入端，有

a[t]=Wx[t]+Vh[t-1]+b

(7)

h[t-1]=φ(a[t-1])

(8)

式中：x[t]为第t时间步的输入；W和V分别为输入到隐层、隐层到隐层的权重矩阵；b为偏置向量；φ(·)为激活函数；a为中间变量。

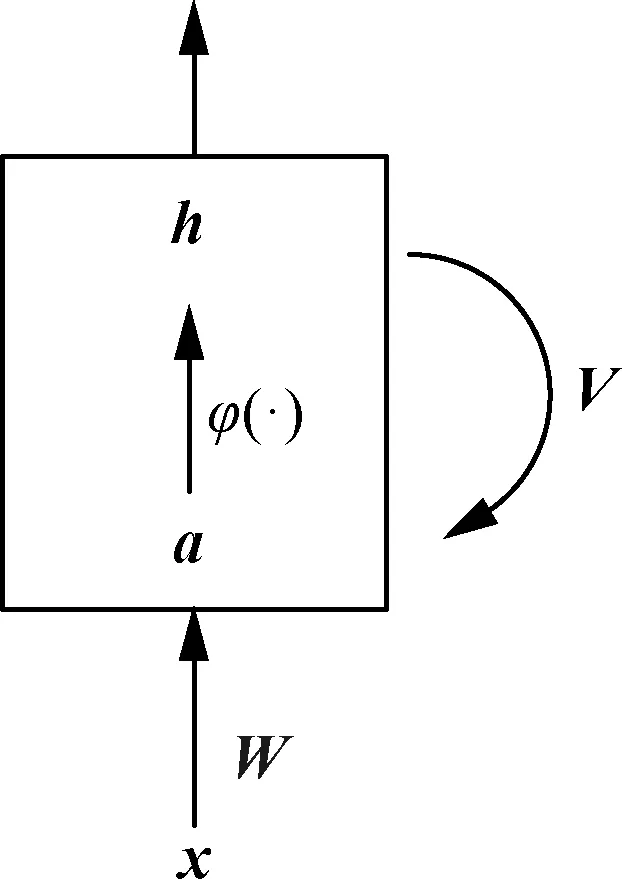
图1 单层RNN结构Fig.1 Structure of a single layer RNN

RNN通过循环方程(Recurrent Formulation)提取序列中的信息，并记录在隐层状态h中，如图2所示。RNN的循环方程为

h[t]=f(h[t-1],x[t],θ)

(9)

式中：θ为给定RNN的参数；f(·)为给定RNN的映射关系。

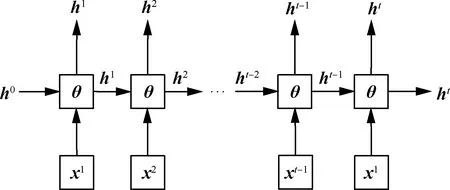
图2 RNN计算图Fig.2 Computational graph of RNN

将RNN的映射关系沿时间轴展开，可得

h[t]=f(h[t-1],x[t],θ)=

f(f(h[t-2],x[t-1],θ),x[t],θ)

…

=g(t)(h[0],x[t],x[t-1],…,x[1])

(10)

式中：g(t)(·)表示RNN在第t步的展开映射关系。

式(10)表明第t步的RNN隐层状态h[t]中蕴含了响应信号序列x[t],x[t-1],x[t-2]…的信息，可以有效地建立响应信号序列的内在关系，获得原系统的信息，进一步处理可以获得原系统的模态参数。

相比参数化模型类方法，由于RNN模型强大的表达能力，采用RNN根据响应信号能更好地挖掘原系统的特性。同时在实际工程结构在线辨识任务中，不必再受参数化模型的最优阶数选择、高斯分布假设等难以满足的约束的限制，提高其工程实用性。

2 基于循环神经网络的时变结构模态参数在线辨识

2.1 长短时记忆网络

由于传统RNN在训练过程中会出现梯度消失或梯度爆炸问题，因此距离当前时刻较远的输入的影响会显著降低。这一特性一方面满足递推辨识任务的基础要求，另一方面历史信息衰减太快，无法实现长期影响，难以有效提取时间序列中的有效信息。为了实现利用适当时间段内历史信息处理序列问题的目的，长短时记忆网络(LSTM)引入内循环，并由输入序列实时决定相关权重[27]。重要历史信息通过存储在内循环中实现长期影响；同时还可以由内循环的操作实现合适的遗忘机制。由于内循环相关权重由输入序列决定，因而可以使得网络在同一组参数的情况下有效处理不同时间尺度的问题。LSTM如图3所示，其前向计算与传统RNN单元相比增加了一个内部状态与3个控制门。第i个LSTM单元在第t时间步时其遗忘门gFi[t]、输入门gIi[t]、输出门gOi[t]以及内部状态si[t]分别为

(11)

(12)

(13)

si[t]=gFi[t]si[t-1]+

(14)

式中：x和h分别表示输入向量和隐层输出向量；b为偏置向量；U和W分别为“输入-内循环参数”和“隐层输出-内循环参数”的权重矩阵；上标或下标中F、I、O和S分别表示遗忘门、输入门、输出门和内部状态相关参数；σ(·)为非线性激活函数sigmoid函数。

其隐层输出为

hi[t]=tanh(si[t])gOi[t]

(15)

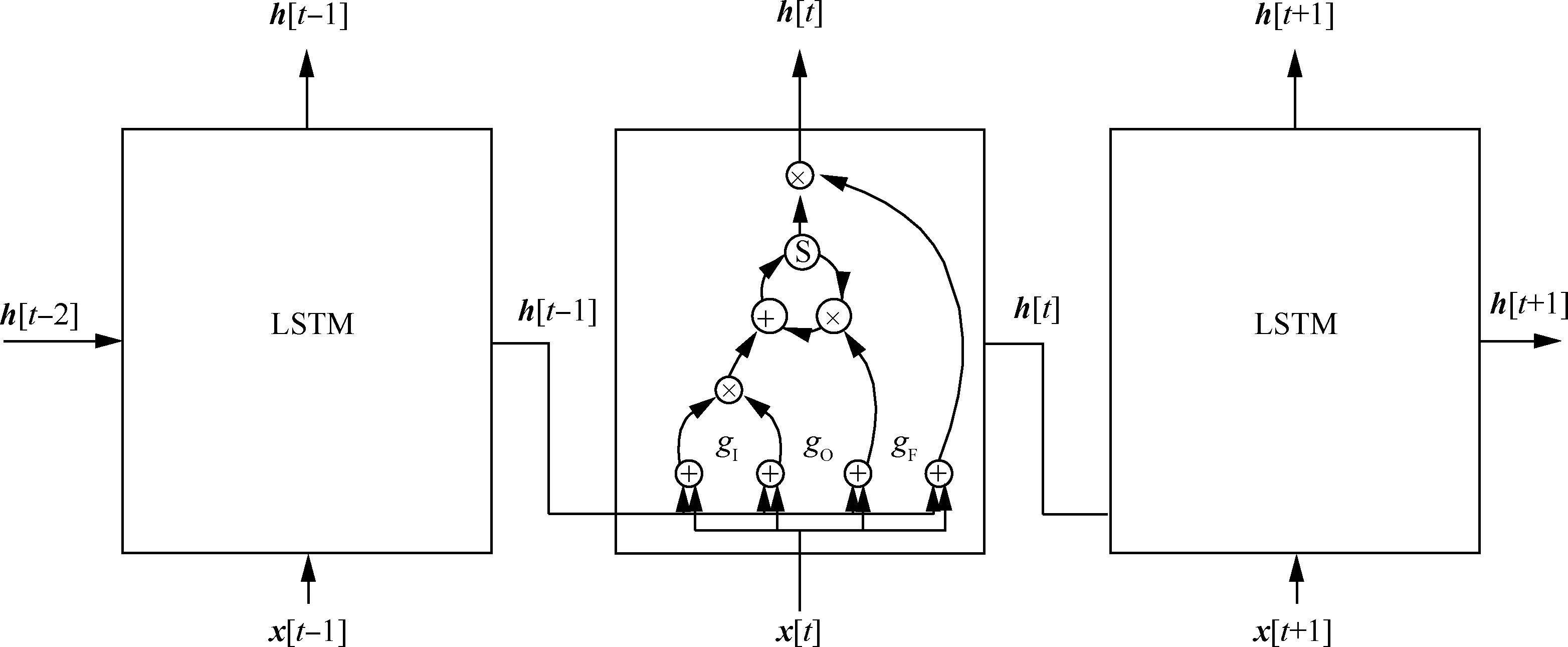
图3 LSTM计算图Fig.3 Computational graph of LSTM

2.2 时变结构在线辨识模型

针对传统递推辨识算法的模型阶数确定难，抵抗实际环境中测量系统由于各种偶发因素产生的脉冲噪声能力有限等问题，根据冻结实验[28](一系列冻结构型的时不变结构动力学实验)结果或是批量辨识方法的结果，并结合先验知识，人工参与地构建数据集用以训练在线辨识的神经网络模型，将先验知识在训练数据集构造过程中离线地引入在线辨识模型，结合网络模型自身特性，有效提升在线辨识的精度与鲁棒性，增强其工程实用性。

在线辨识网络模型基本结构由输入层、LSTM层和全连接层组成，其中输入层为线性层，全连接层中最后一层为线性层，其余为非线性层，非线性激活函数为修正线性函数(Rectified Linear Unit,ReLU)，如图4所示。

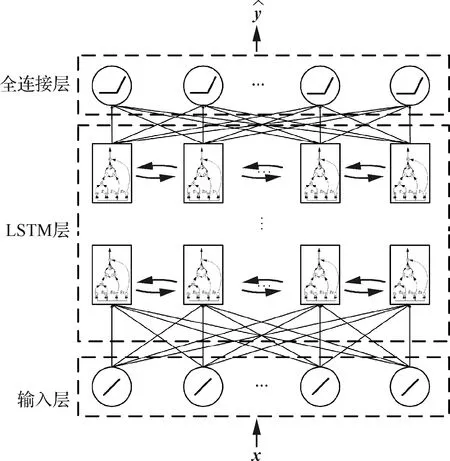
图4 在线辨识网络模型Fig.4 Online identification network model

在网络模型训练阶段，定义损失函数为

(16)

通过求解参数优化问题:

(17)

获得网络模型参数θ的最优估计，确定用于时变结构模态参数辨识的网络模型。采用Adam算法实现优化过程。此外，优化问题的初值采用Xavier方法[29]获得，LSTM的隐层初始状态全部假设为零状态。

通过离线训练阶段获得网络模型参数θ后，辨识任务相关的离线知识全部蕴含在参数θ中。在线辨识阶段网络模型根据每一时刻输入的振动响应建立时序关系，计算待估模态参数。同时在网络模型在线辨识过程中，只进行有限次代数计算，不包括优化、矩阵求逆、特征值计算等复杂迭代过程，在线辨识的实时性得到保证。

3 时变结构模态参数实验验证

航空航天工程中广泛存在空中加油[30]、质量矩控制[31]等质量大范围转移的动力学过程，为验证方法的有效性，本文采用可以有效反映这类质量转移过程的移动质量梁时变实验系统，在由质量块移动产生的激励作用下生成非平稳振动信号，用以在线辨识时变结构模态参数，并与冻结实验获得的基准结果以及基于TARMA模型的递推最小二乘方法[32](TARMA-RLS)获得的结果进行对比。

3.1 时变结构实验系统

移动质量梁实验系统主要由质量块、简支梁及其支撑结构、电机系统以及数据采集系统等部分组成，如图5所示。梁两端简支，长2 m，截面为60 mm×10 mm的矩形；质量块外轮廓尺寸为80 mm×100 mm×70 mm；梁与质量块材料均为钢。在实验过程中，质量块可由两端电机牵引在简支梁上沿梁的轴向滑动。质量块的运动规律可由控制器事先设定，控制两端电机运动实现不同的结构动力学特性时变过程。沿梁的轴向均匀布置15个型号为333B30的压电式加速度传感器(示意图中只标出3个)，采用激光测距仪测量质量块在运动过程中的轴向位置，通过SCADAS Ⅲ数据采集系统进行振动数据的采集与记录。采用上升沿触发，使电机牵引与数据采集同时开始，采样频率为512 Hz，记录时长为256 s。

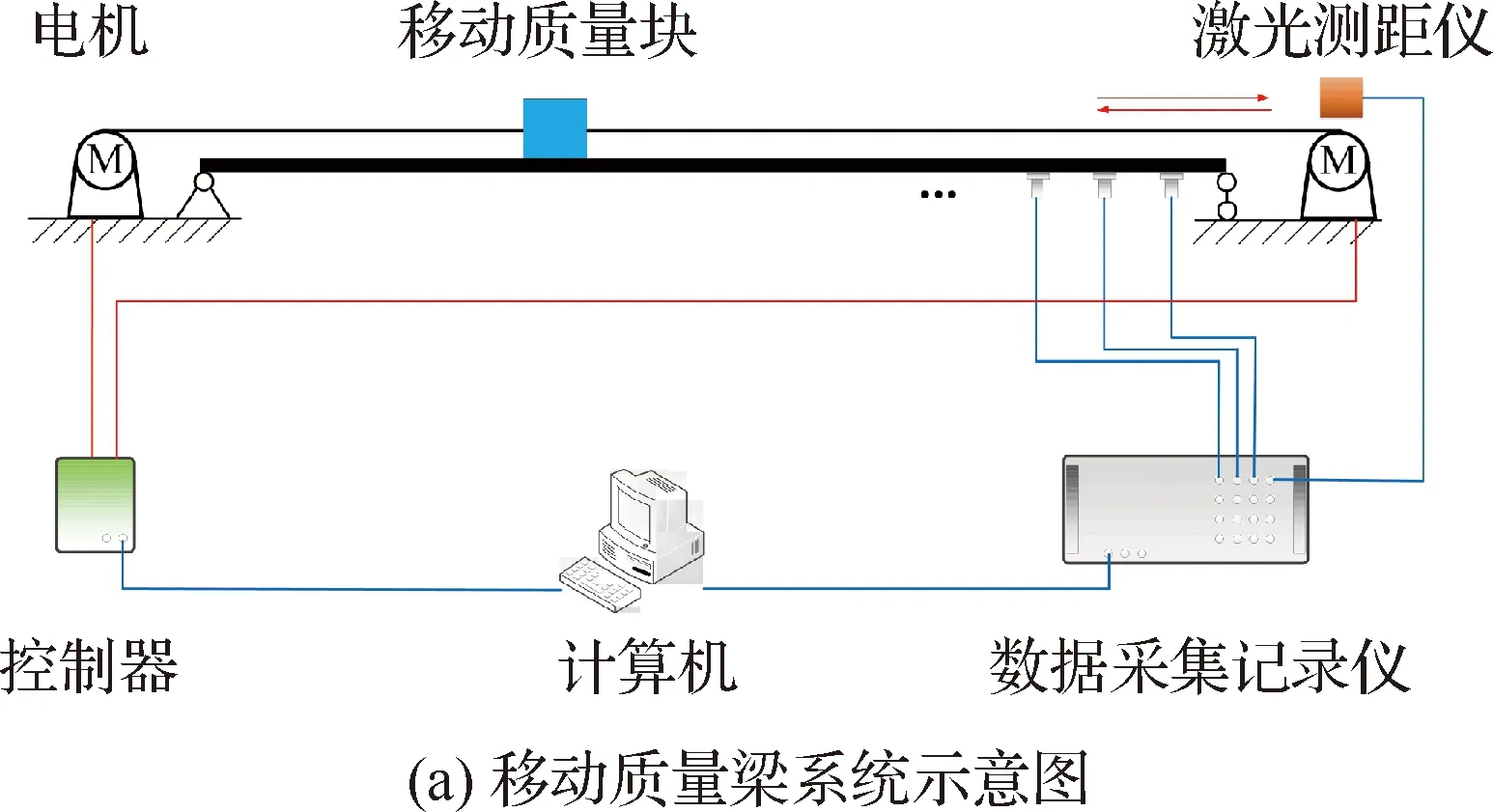
图5 移动质量梁实验系统Fig.5 Experimental system of moving-mass beam

3.2 在线辨识网络模型建立

3.2.1 “冻结”实验及基准模态参数

在其他条件不变的情况下，移动质量梁实验系统的结构动力学特性完全由质量块的位置决定。当质量块处于某一位置固定不动，即系统处于某一“冻结构型”时，可以采用针对线性时不变系统的模态实验方法获得当前构型下的系统模态参数，用来作为时变系统的基准。将质量块从距离简支梁右端25 cm处开始，每隔5 cm进行一次冻结实验，共进行31组实验，获得系统结构模态参数随质量块位置的关系。其中系统固有频率随质量块位置变化关系如图6所示，图中从下至上依次为第1阶到第6阶固有频率。

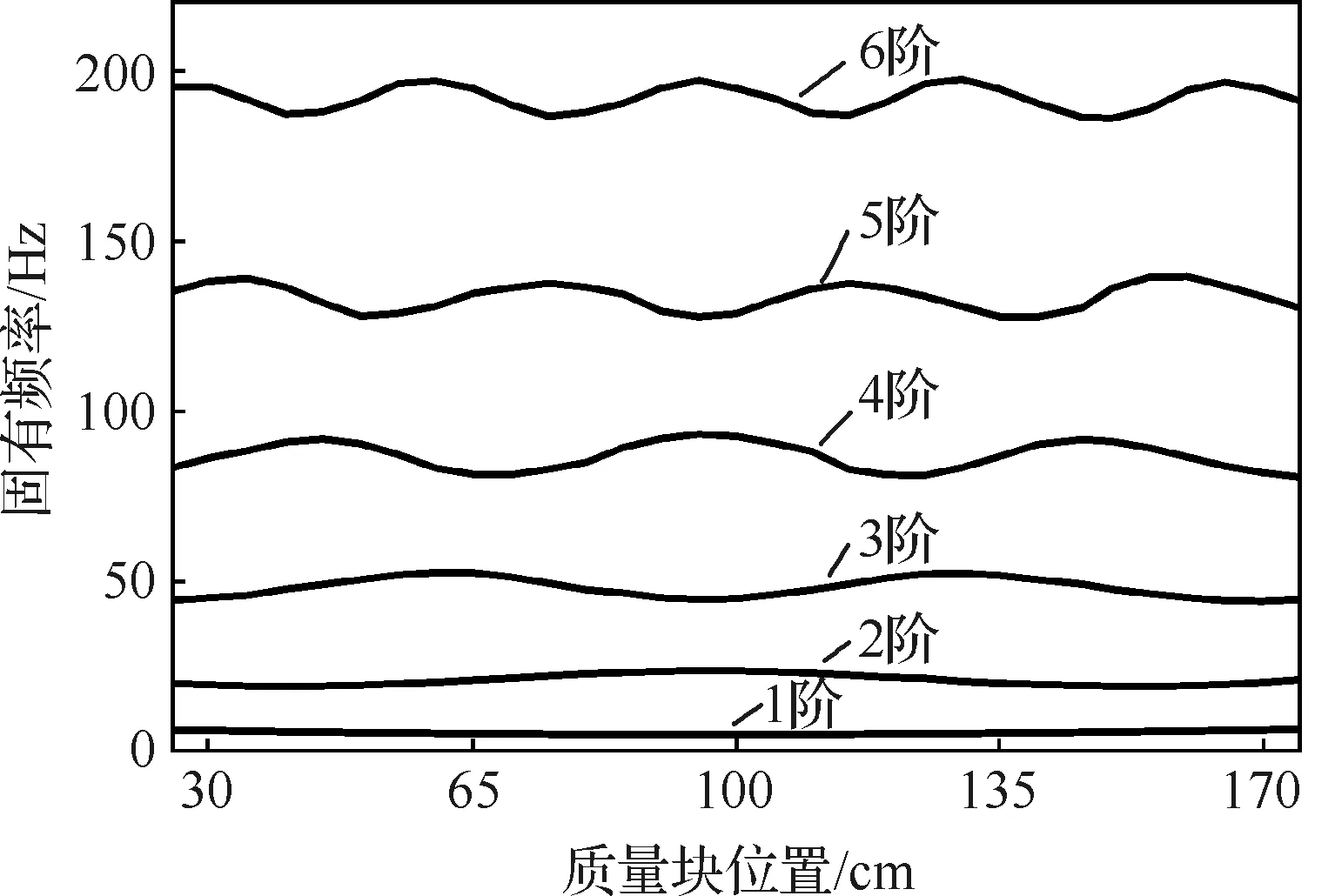
图6 固有频率随质量块位置变化关系Fig.6 Natural frequencies varying with mass position

3.2.2 时变实验及辨识模型建立

实验中，质量块的运动规律由质量块行程(由质量块距简支梁左右两端的最小距离LL和LR表示)和质量块移动速度(由电机转速r1和r2表示)来描述。训练集数据由LR=LL且分别为30、50和70 cm，转速r1=r2且分别为100、200、300、400、500和600 r/min即18种质量块运动规律，每种重复3次，共54组实验数据组成。验证集数据由LR=LL且分别为40和60 cm，转速r1=r2且分别为100、200、300、400、500和600 r/min即12种质量块运动规律，此外还包括LR=LL=45 cm，转速(r1,r2)分别为(150,350)r/min、(250,500)r/min、(450,250)r/min和(450,350)r/min 4种非匀速运动规律，每种1次，共16组实验数据。其中LR=LL=40 cm，r1=r2=200 r/min工况中8号传感器所测非平稳振动时域响应如图7所示。

图7 非平稳振动响应Fig.7 Non-stationary vibration signal

根据冻结实验得到的系统模态参数随质量块位置的关系以及激光测距仪获得的质量块位置，通过插值得到每一时刻系统的模态参数。在线辨识网络模型的输入为第2、4、6、8、10、12和14共7个加速度传感器的测量值，期望输出为系统的前6阶固有频率，对非平稳随机振动响应的加速度信号采用均值与方差进行数据归一化，对输出的频率采用最大值进行归一化，以此建立数据集。

根据2.2节中的在线辨识网络模型，取输入层线性单元50个，LSTM部分共3层，每层50个LSTM单元，全连接部分非线性层一层，50个非线性单元，通过数据集训练即可得到针对该移动质量梁时变结构模态参数的在线辨识网络模型。

3.2.3 辨识结果

为了定量评价辨识结果，定义平均绝对误差(Mean Absolute Error,MAE)为

(18)

在验证集上的辨识结果如表1所示,在线条件下，结合离线知识的辨识模型可以对结构模态参数进行准确的估计,平均绝对误差为1.06×10-3。同时单步平均估计时间5.36×10-5s小于物理采样间隔1.95×10-3s (512 Hz)，证明了其具有在线辨识的能力。选取误差最大的2组数据，工况1为(40 cm,40 cm,600 r/min,600 r/min),工况2为(45,45,450,250),其质量块移动规律和辨识结果如图8所示。对比2种工况可以得到，质量块不同的运动规律导致系统固有频率产生不同的变化规律，在线辨识网络模型根据加速度响应均可以给出较好的估计结果。较大误差出现在状态突变处(本算例中为质量块移动到最大行程处突然转向)，主要是由于LSTM隐层状态变量没能及时反映突变后的动力学状态，导致估计误差偏大。计算若干时间步，隐层状态得到充分更新，在线辨识网络模型自动恢复辨识精度。类似地，如图8(g)和图8(h)所示，在辨识初始阶段由于LSTM内部状态的初值是人工设定的，不符合物理系统，所以误差较大，但递推计算一段时间后，内部状态充分更新，辨识精度提高。

表1 辨识模型在验证集的辨识结果Table 1 Results of identification model on valid set

图8 在线辨识结果Fig.8 Online identification results

为考察网络模型的结构鲁棒性，在其LSTM层分别为2、3、4层以及每层单元数分别为30、50和70的情况下，辨识平均误差以及最大误差如表2所示，辨识结果精度基本相当，表明模型结构具有一定的鲁棒性。

表2 网络模型结构对辨识精度的影响Table 2 Influence of network model structure on indentification accuracy

前述训练集与验证集中表征质量块移动速度的电机转速变化范围均在100～600 r/min之间，为了进一步验证方法的适用性，补充实验工况LR=LL=40 cm,r1=r2=700 r/min，其辨识结果如图9所示，其MAE=2.05×10-3，与验证集精度相当，但误差确有增大。结果表明本文方法具有一定的适应性，但为了保证辨识的精度与可靠性，在建立数据集时应尽量覆盖到结构的实际运行状态。

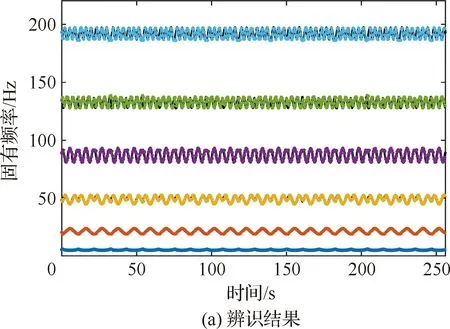
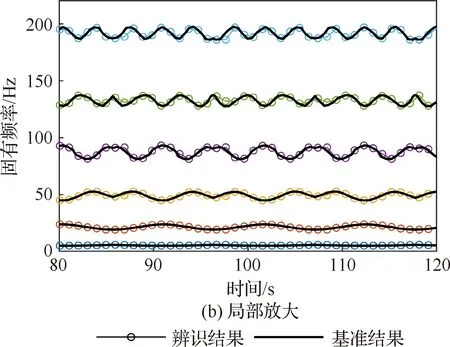
图9 未覆盖工况辨识结果Fig.9 Identification results of unconsidered motion states

3.3 讨 论

时变结构模态参数在线辨识方法应用到复杂工程结构中会面临很多实际问题。在线辨识的结果通常会作为控制、健康监测等任务的直接输入，一方面要求辨识方法计算效率满足实时性要求，另一方面要求辨识结果具有连续性，即在每一个时间步必须给出一个可靠的估计结果。在抗虚假结果能力和抗脉冲噪声2项任务中与经典TARMA-RLS方法进行对比，说明优势。同时本文辨识模型也可以有效满足工程实际中需要获得特定模态参数的需求。

3.3.1 抗虚假结果能力

所有参数化辨识方法都至少包含1个反映模型阶数的参数，直接决定当前模型的特征值数量，决定辨识得到的结构模态数量[33]。不同于数值算例，针对实际结构的振动响应的辨识问题中很难确定最优的模型阶数。若模型阶数偏低，将无法有效获得信号中的主要模态信息；若模型阶数偏高将产生大量虚假模态。参数化辨识方法在实际应用中需要对虚假结果进行筛选，但会导致辨识结果的不连续。而结合离线知识的辨识网络模型由于在离线训练过程中所采用的训练数据是加入大量先验知识以及人工参与的方法构建的，在其在线辨识过程中可以有效缓解虚假结果问题，获得可靠的在线辨识结果，供下游专业使用。

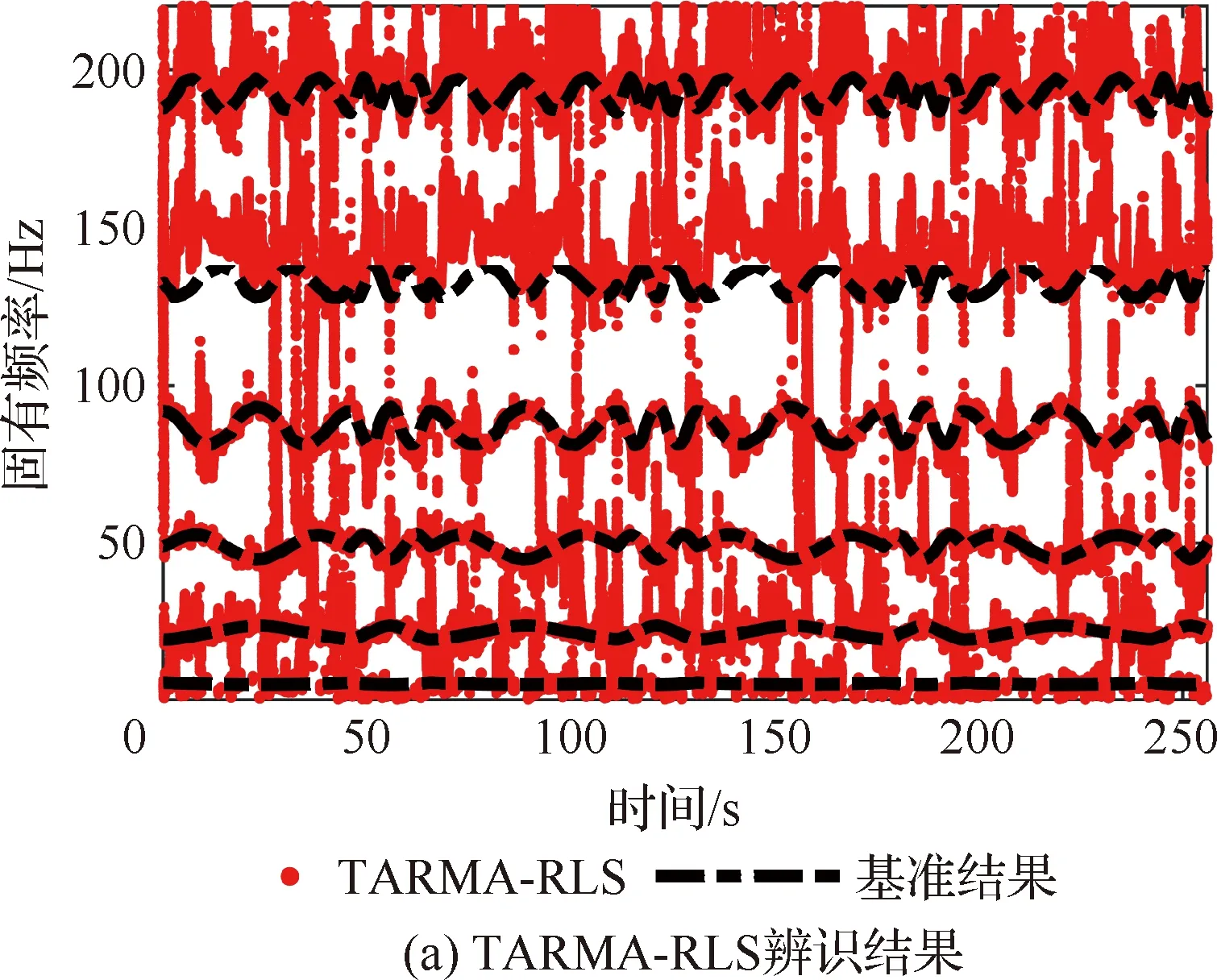
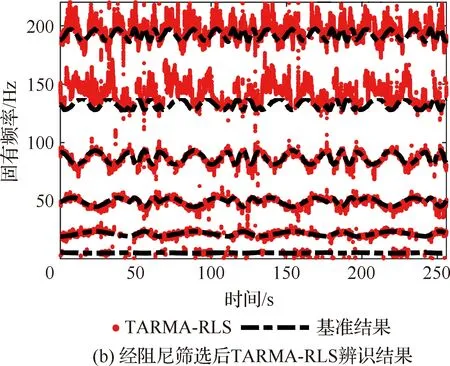
质量块运动规律为LR=LL=45 cm，r1=150 r/min，r2=350 r/min的工况，采用TARMA-RLS方法，AR阶数取2，MA阶数取1，遗忘因子取0.99，辨识结果如图10所示。图10(a)和图10(b)分别为采用TARMA-RLS方法辨识结果以及采用阻尼比0.1筛选结果。显然辨识结果存在大量虚假模态，而经过筛选后部分模态参数缺失严重。图10(c)为本文方法辨识结果，由于在离线训练过程中已经引入先验知识，因此每一个时刻都能获得较为准确的模态参数估计。

3.3.2 针对脉冲噪声的鲁棒性

在实际工程应用中，振动测量系统受到成本、传输、环境适应性等方面的限制，其测量精度无法达到实验室条件下的精度。同时在实际运行过程中还会受到自然因素和人为因素的干扰，产生较强的冲击干扰，其在线测量结果中往往会包含脉冲噪声(远离数据的极端异常值，即野点)。这类脉冲噪声不服从高斯分布，是一类非高斯噪声。而传统参数化结构模态参数估计方法通常基于高斯分布假设，在处理这类测量信号中包含脉冲噪声的在线辨识问题时难以给出较好的模态参数估计结果。

基于LSTM的在线辨识网络模型对数据中包含极端异常值的问题具有一定的鲁棒性。主要是由于异常数据进入LSTM单元后，在输入、更新隐层状态以及输出等步骤中均会经过具有“饱和”效应的非线性激活函数sigmoid函数或是tanh函数，如图11所示。极端数据的不利影响在经过非线性激活函数后被有效抑制，使得基于LSTM的在线辨识网络模型应用于实际工程结构的在线辨识任务中具有更强的鲁棒性。

由于在实验室条件下难以复现实际工程结构中各种干扰导致的数据极端异常值，为验证在线辨识网络模型在抗脉冲噪声方面的鲁棒性，采用在现有实验数据中增加数值脉冲噪声的方式来模拟。α稳定分布常用来对脉冲噪声进行建模[34]，其特征函数为

(19)

式中：α为分布的脉冲程度；β为分布的偏斜程度；γ为分布的离散程度，类似于“方差”；μ为其分布的位置，类似于“均值”。

以质量块运动规律LR=LL=60 cm，r1=r2=100 r/min为例，α稳定分布参数取α=0.8，β=0，γ=1×10-5，μ=0，生成脉冲噪声添加到实验数据中，8号传感器加速度响应加入脉冲噪声前后对比以及局部放大如图12所示，加入α稳定分布产生的噪声后，对原信号大多数时刻几乎无影响，只在个别时刻产生显著的偏差，可有效模拟脉冲噪声。

为进一步评估本文方法的抗脉冲噪声能力，针对α=0.8，β=0，μ=0，γ分别取1×10-3、1×10-5以及1×10-7这3种分布，分别进行10次计算，其辨识结果如图13所示。

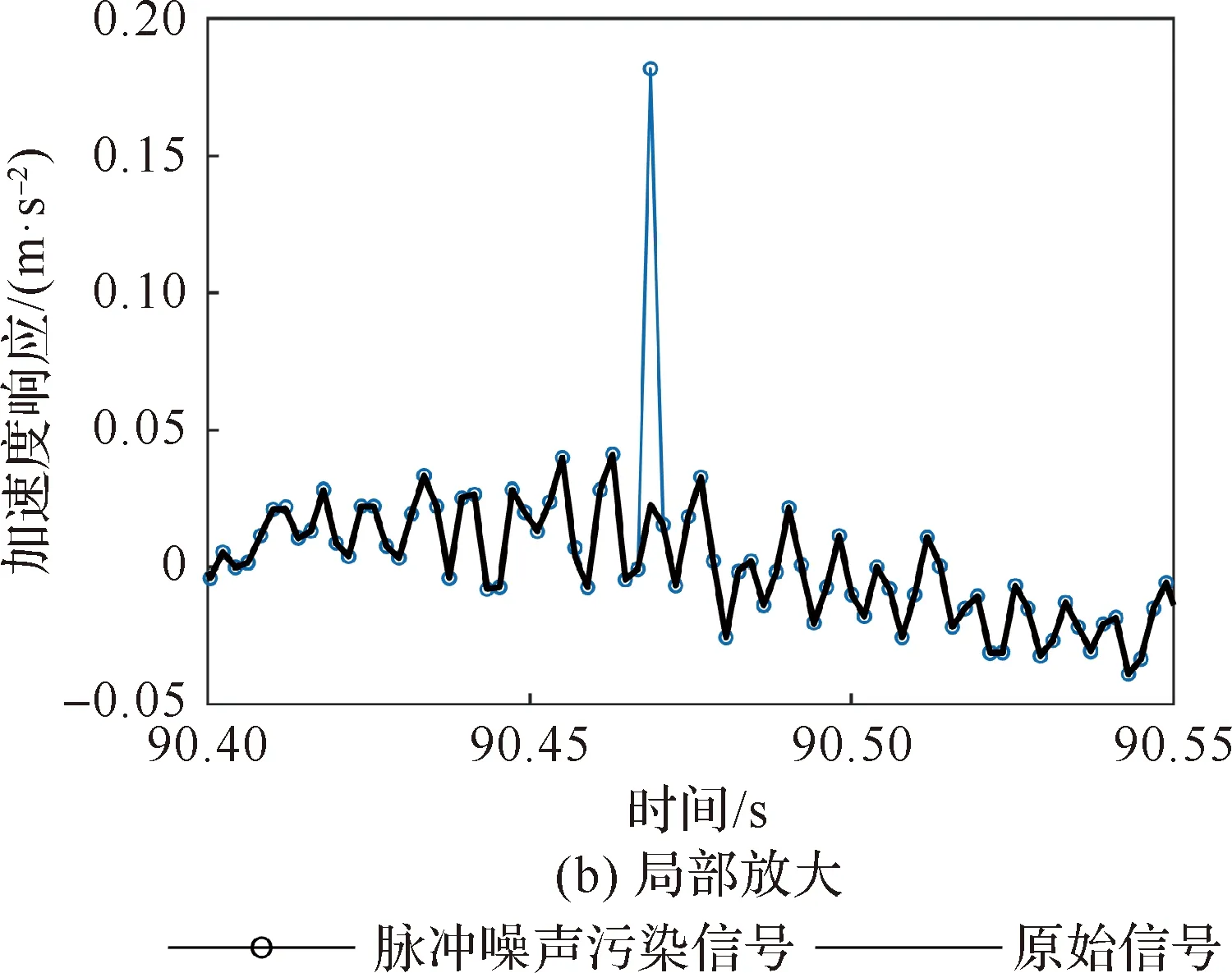
图12 脉冲噪声污染信号Fig.12 Signal with impulse noise

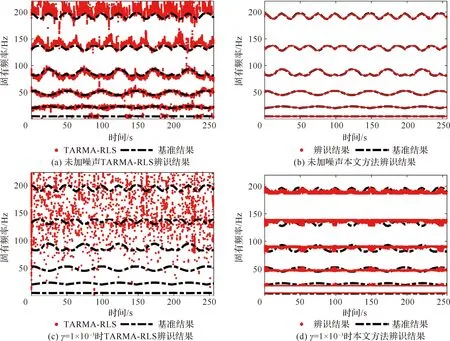
图13 包含脉冲噪声的辨识结果Fig.13 Identification results with impulse noise

与基准结果相比，在γ=1×10-3时，在强噪声的干扰下，TARMA-RLS方法与本文方法均失去了模态参数的估计能力。在γ=1×10-5时，TARMA-RLS方法的10次辨识结果分散，虚假结果严重，而本文方法可以有效跟踪时变规律。当噪声进一步减少到γ=1×10-7时，2种方法的辨识结果与未加脉冲噪声的辨识结果基本相当，但本文方法在抗虚假结果、辨识结果的连续性等方面仍具有优势。

3.3.3 特定模态参数辨识

控制或健康监测等任务通常关注特定模态参数[1,5]。若采用传统辨识方法直接从振动信号中辨识全部模态信息，挑选工作需要在线进行，难以实现。

为实现准确高效地针对特定模态参数的在线辨识任务，可以充分利用先验信息，将模态参数挑选知识离线地赋予在线辨识网络模型，这样可以有效提升在线辨识任务的质量。在构建训练数据集时，期望输出不再为全部阶模态参数，而是根据任务要求先验地挑选结果，采用类似的方法建立在线辨识网络模型，以关注第2阶、第6阶固有频率以及第2阶模态振型变化为例，其验证集中平均MAE为2.28×10-3，最大MAE为3.06×10-3，误差最大的工况对应的质量块运动规律为LR=LL= 40 cm，r1=r2=600 r/min，其结果如图14 所示。在离线地引入先验知识后，针对结构特定模态参数的在线辨识模型可以高效准确地获得所需模态参数。

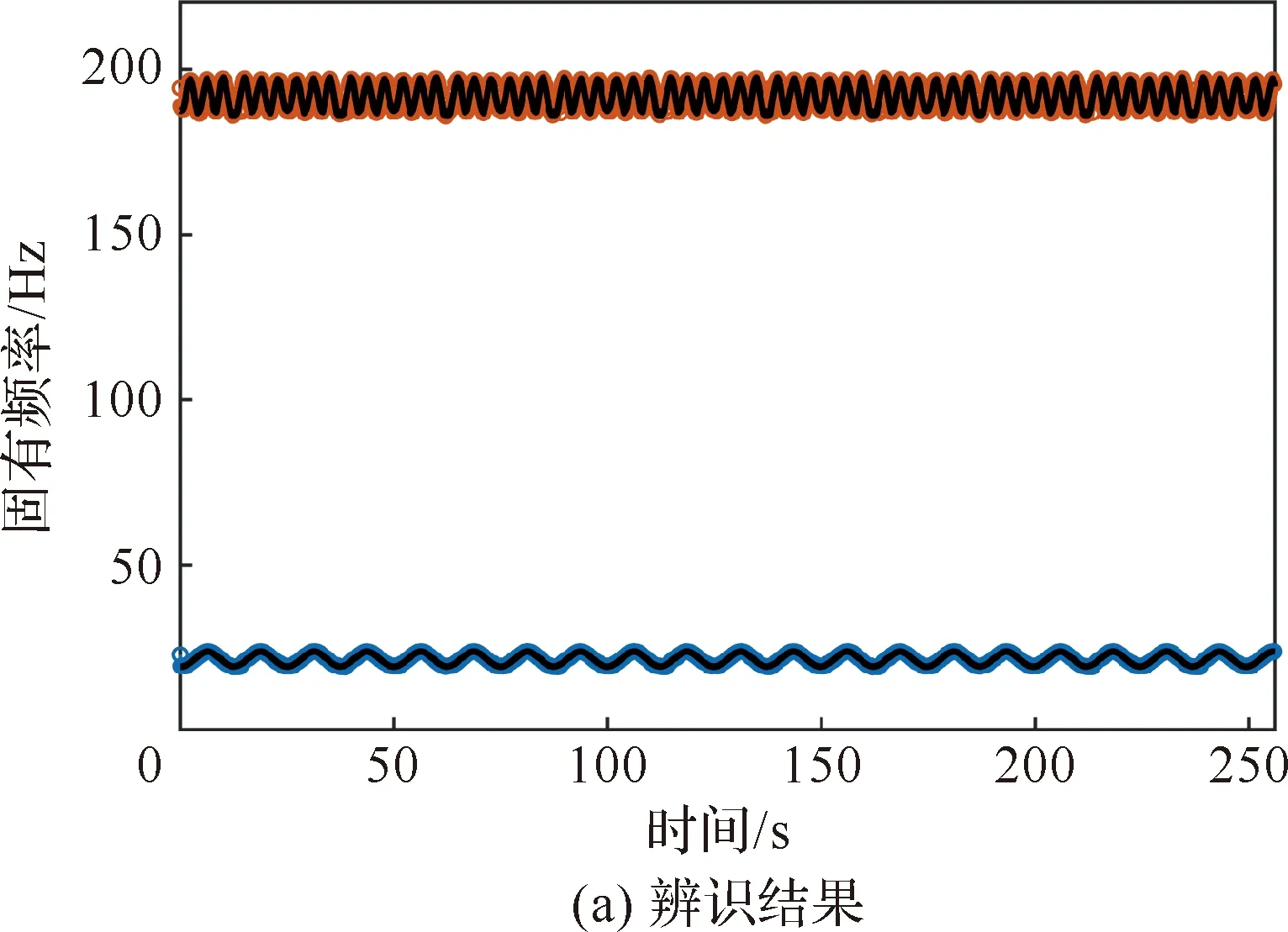
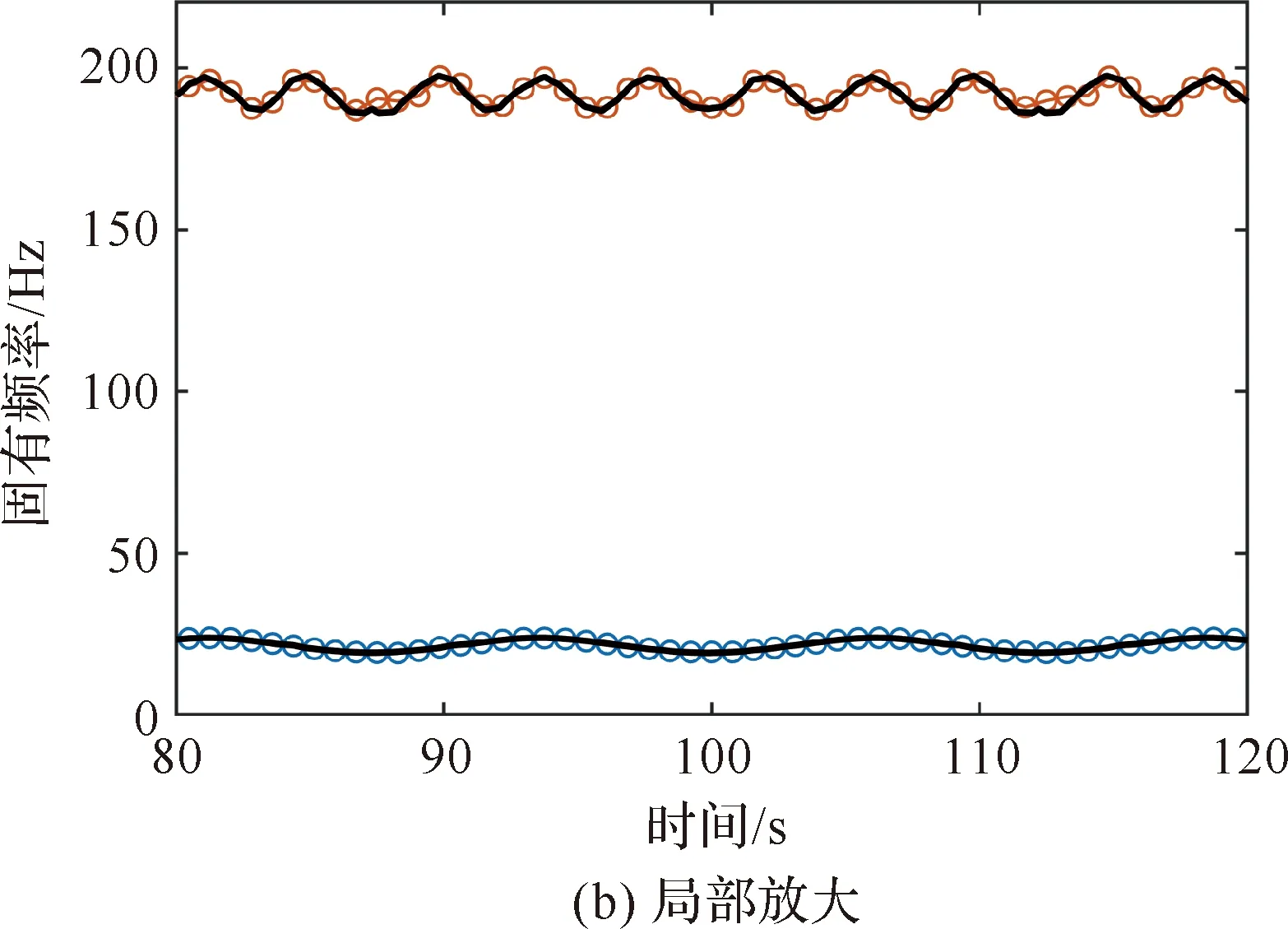
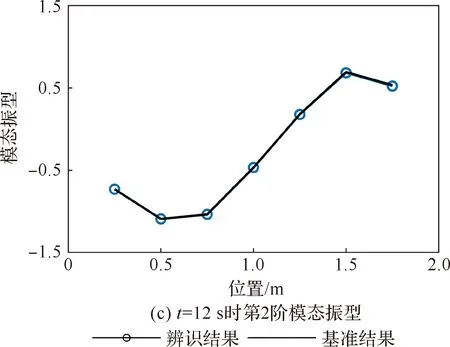
图14 针对特定模态参数的辨识结果Fig.14 Identification results for specific modal parameters

4 结 论

1)本文建立了基于LSTM的在线辨识网络模型，结合离线知识，可以从非平稳振动响应数据中高效、准确地估计得到时变结构在不同时变规律下模态参数，并通过移动质量梁时变实验系统验证了方法的有效性。

2)与传统参数化时变结构模态辨识方法相比，基于LSTM的在线辨识网络模型由于包含了时变结构的先验信息，在相同数据条件下有效减少了虚假结果，同时保证了辨识结果的连续性，给出较为可靠的估计结果，对于控制系统、结构健康监测等对时序与稳定性高要求的在线应用场景十分重要。

3)在实际工作条件下，工程结构模态参数在线辨识会遇到由于各种因素导致的测量数据包含极端异常值(野点)，这类脉冲噪声不符合高斯分布，LSTM内部的“饱和”特性使得其对此类问题具有一定的鲁棒性。基于LSTM的在线辨识网络模型可有效应对测量数据中包含的脉冲噪声，提升在线辨识的鲁棒性。