C/C复合材料的压缩强度分布与可靠性评估
李湘郡,李彦斌,郭飞,吴邵庆,*
1.东南大学 空天机械动力学研究所,南京 211189 2.东南大学 土木工程学院,南京 211189 3.东南大学 机械工程学院,南京 211189
碳/碳(C/C)复合材料作为纤维增强复合材料中的一种新型材料,以密度低、比强度和比模量高、膨胀系数低、热传导性和断裂韧性好、耐磨、耐烧蚀等优点,被广泛应用于航空航天、核能、化工及医疗等领域。但由于C/C复合材料中碳纤维的种类、取向、含量以及制备工艺等的差异性,导致其力学性能存在较大的离散性,其中强度作为表征材料综合力学性能的重要指标[1],同时也是结构设计中的一项重要参数,其离散性势必会限制结构的高可靠性设计。工程上一般通过增加材料的用量来提高结构的强度可靠性,而对于轻量化要求较高的飞行器结构,这会严重制约飞行器的总体设计和结构设计。基于统计分析的方法研究C/C复合材料的强度分布规律,可为飞行器结构的轻量化和高可靠性设计提供有效的解决途径。
对于碳纤维增强复合材料的强度分布,国内外学者已开展了大量研究,周亚东[2]、陈素芳[3]等研究了C/SiC材料的疲劳性能;Calard和Lamon[4-5]采用概率统计方法描述了2D编织SiC/SiC陶瓷基复合材料断裂强度的分布规律;Lu等[6]采用Weibull分布和正态分布分析了脆性材料断裂强度的统计特征。针对碳纤维增强复合材料中C/C复合材料的强度分布,也有不少学者开展了研究,郭飞等[7]用Weibull模型拟合了C/C复合材料的剪切强度分布;Basu[8]和严科飞[9]等认为Weibull分布对于脆性材料的强度分布拟合结果较为精确。近年来,关于Weibull分布是否为C/C复合材料强度分布的最优拟合这一问题,专家和学者们也开展了大量研究工作,Basu等[8]通过极大似然方法分析了多组数据在不同分布模型下的参数,并用极大似然准则、最小距离准则及卡方检验来比较各分布模型的优劣性;Dey和Kundu[10]对比了Weibull分布、正态分布以及对数正态分布,并通过Kolmogorov-Smirnov(K-S)检验确定最优拟合。在C/C复合材料的强度分布研究中受到经济成本和时间成本的限制,实际研究的样本数量有限,而样本数量对于强度分布参数的求解精确度有较大的影响,Danzer[11]分析了小样本数量陶瓷基复合材料脆性断裂的强度分布,发现样本数量较小时,由拟合所得Weibull分布计算所得的材料强度高于材料的实际强度;Pai和Gyekenyesi[12]研究发现样本数量对于Weibull分布的尺度参数和形状参数的求解精度有着较大的影响。目前的研究中,常用的参数估计值求解方法与检验方法均较为单一,求解参数估计值时通常采用极大似然法,并通过K-S检验来证明结果的精度。然而极大似然法计算较为繁琐,且样本数量是否会影响穿刺C/C复合材料强度分布分析结果的精度,目前对这一问题的研究尚且不多。
针对以上问题,并考虑到碳纤维复合材料力学性能离散的特点,本文采用一种新的方法,即残差分析方法来确定可以满足穿刺C/C复合材料强度分布分析结果精度要求的样本数量;选择线性回归分析法获得两参数Weibull分布、正态分布和对数正态分布模型的参数,与极大似然法相比,线性回归分析法思路更清晰、计算更简便;最后,除最常用的K-S检验外,本文还采用了Anderson-Darling(A-D)检验与极大似然检验方法进行拟合精度检验,进一步确保结果的准确性。
1 试验样本数量确定
研究采用的试件由四川骏瑞碳纤维材料有限公司提供,试件为尺寸15 mm × 15 mm的穿刺C/C复合材料,制备材料为T300碳纤维,单层碳布采用平纹编织。其制备工艺为:首先,将单层0°无纬布、胎网、90°无纬布、胎网循环铺层到一定厚度时,沿垂直于碳布方向进行针刺,制成三维预制体;其次,采用化学气相渗透(CVI)工艺对所得预制体进行致密化处理,得到未石墨化处理的C/C复合材料;然后,将复合材料置于高温环境中进行石墨化处理;最终,通过机械加工的方式获得C/C复合材料试件,其密度在1.55 g/cm3左右。
由于C/C复合材料制备工艺复杂、制备周期长且制备成本较高,试验所采用的样本数量受到限制。而不少学者指出,样本数量会对材料强度分布拟合式(如正态分布、对数正态分布、伽马分布或Weibull分布等)的精确度造成影响,其中,Xu等[13]研究了样本数量对Weibull分布形状参数和尺寸参数的影响,指出用于表征材料强度分布的样本数量最少不应低于20;Danzer[14]和Nohut[15]等将氧化铝的强度试验值与采用Monte Carlo模拟得到的强度拟合值进行对比分析,指出应至少通过30个试样的强度数据来确定Weibull参数,以保证拟合所得Weibull参数在合理的标准偏差范围内。因此,如何采用有限数量的试验样本数量来准确表征穿刺C/C复合材料的强度分布非常关键。本文通过残差分析来确定强度分布分析所需的最小样本数,以保证所得强度分布和可靠性分析结果的精度。
残差分析通常用于验证所假设的分析模型的正确性[16]。所谓残差即实际观测值与理论拟合值之间的差,可表示为
(1)

(2)
前期对穿刺C/C复合材料的研究中,已通过剪切试验得到了穿刺C/C复合材料的剪切强度数据[7],试验在美国Instron公司生产的3367双立柱电子万能试验机上进行,加载速率为0.5 mm/min。由于碳纤维复合材料的剪切强度具有各向异性,而该试验在单个方向的样本数量仅为20,本文分析所需的样本数量较多,故将加载方向也作为引起材料强度离散性的因素之一,采用5个方向的剪切强度数据来分析,试件总量为100,由此得到100 个强度试验值如表1所示。每隔 10 个样本点计算不同样本数时的残差值,并进一步获得残差的均值如表2所示,由于残差均值可能会出现负值,为便于分析,图1给出了残差均值的绝对值随样本数量的变化趋势。
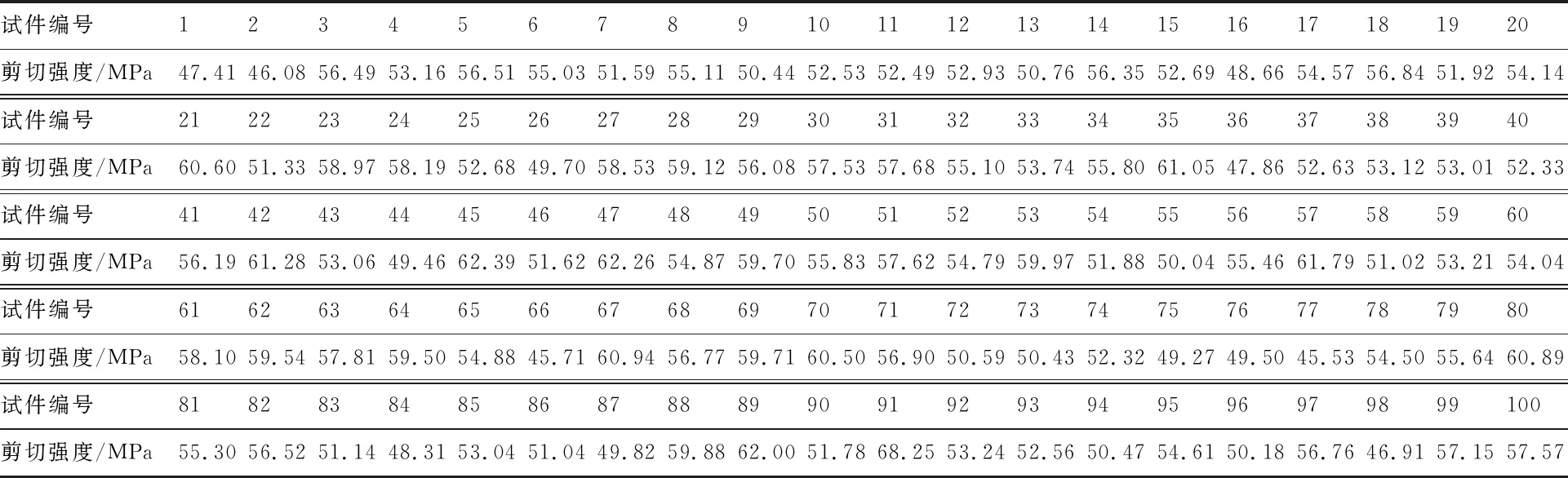
表1 穿刺C/C复合材料剪切强度试验数据Table 1 Datas for shear strength test of punctured C/C composites
针对穿刺C/C复合材料,分析图1可知:① 随着样本数量的增加,样本残差的均值总体上呈稳定下降趋势;② 当样本数量少于30时,其残差均值明显高于样本数量大于或等于30时的残差均值,然而样本数量为20和30时残差均值绝对值发生突变并不是一般规律,是由于试件的强度离散性导致的;③ 当样本数量为30或更多时,残差均值较小且收敛,并在样本数量达到50时,均值的数量级由10-14变为10-15,表示所得分布模型的精度逐渐提高。结合以上残差分析的结果,并兼顾经济和时间成本,确定本文强度分布分析所采用的压缩试验样本数量为30个。

表2 残差均值Table 2 Residual mean value
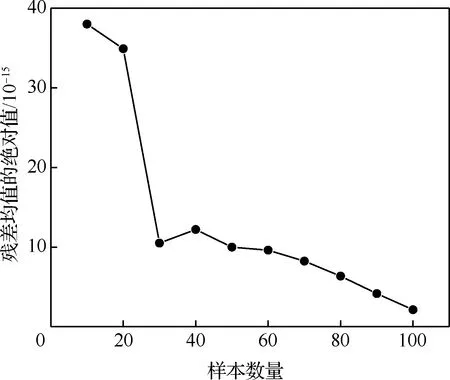
图1 残差均值随样本数的变化曲线Fig.1 Variation curve of residual mean value along with sample size
2 强度分布分析
考虑到剪切试验对试样的要求更高[17],在试验过程中需要考虑的因素更多、操作更复杂[18],因此剪切强度相对于压缩强度,其数据分散性更大,故本文用剪切试验残差分析得到的样本数量代表压缩强度试验的样本数量来进行分析。
由于C/C复合材料具有各向异性这一特征,其在不同方向上的压缩力学性能存在差异,且沿碳布内纤维方向的压缩强度低于垂直碳布内纤维方向的压缩强度,为研究穿刺C/C复合材料的面内压缩强度,加载方向沿碳布内纤维方向,在MTS电子万能试验机[19]上进行压缩试验,加载速率为0.2 mm/min[20],得到30个穿刺C/C复合材料试块的压缩强度试验数据如表3所示。
2.1 强度分布模型
考虑到残差分析适用于分析回归模型,故本文采用线性回归分析方法对试验所得压缩强度值进行分析,拟合常用的Weibull分布、正态分布和对数正态分布。

表3 穿刺C/C复合材料压缩强度试验数据Table 3 Datas for compressive strength test of punctured C/C composites
将Weibull分布、正态分布和对数正态分布模型的概率累积函数进行变换,得到y=a+bx的形式,如表4所示[1]。表4中第2列即为各分布模型的概率累积函数F(S),对表3中的压缩强度试验数据按表4所示形式进行变换,并进行线性回归分析,结果如表5所示。Weibull分布、正态分布和对数正态分布的回归方程依次为
yWE=-60.41+13.47x
(3)
yN=-11.00+0.129x
(4)
yLN=-47.01+10.58x
(5)
表5中判定系数R2为相关系数r的平方,其中相关系数r为
(6)
式中:Cov(x,y)为x与y的协方差;Var(x)为x的方差;Var(y)为y的方差。相关系数r体现了研究变量之间的线性相关程度,线性回归中通常使用判定系数R2表征线性回归拟合程度,其值范围为[0,1]。判定系数R2越接近于1,表明线性回归拟合程度越高。

表4 3种概率分布的线性回归变换关系[1]Table 4 Relations of linear regression transform of three probability distributions[1]
注:S为样本数据;(x,y)为由样本数据转换得到的数据,对其线性回归分析得到斜率b和截距a;μ、σ为不同分布类型的参数;Φ-1为反函数。
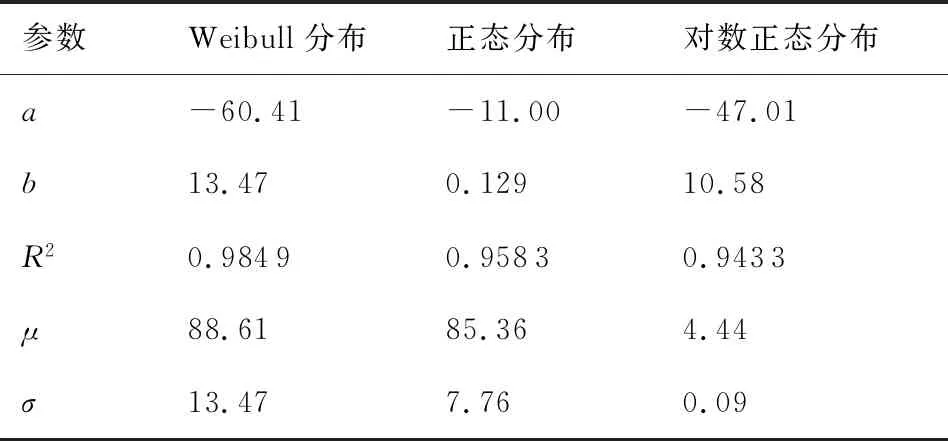
表5 线性回归分析结果Table 5 Analytic results of linear regression
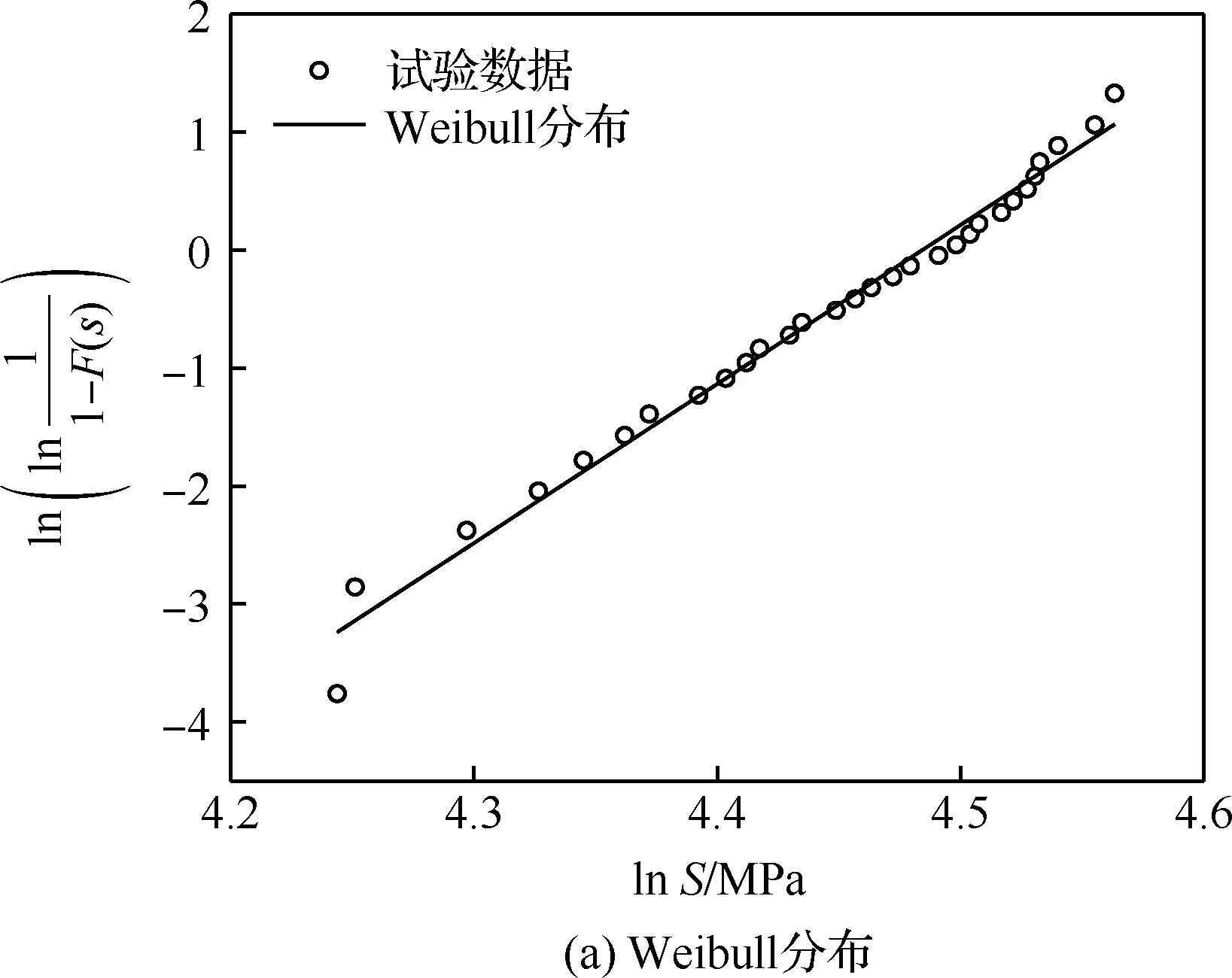


图2 3种概率分布的线性回归分析Fig.2 Linear regression analyses of three probability distributions
据表5中线性回归分析结果可得Weibull分布、正态分布和对数正态分布的回归直线如图2所示。结合表5和图2分析可知:
1)Weibull分布、正态分布以及对数正态分布通过线性回归分析法得到的拟合结果,其线性回归判定系数R2均大于0.9,表明上述3种强度分布模型均可以准确表征穿刺C/C复合材料的压缩强度分布规律。
2)Weibull分布的R2值高于正态分布与对数正态分布的R2值,说明在线性回归分析所得拟合直线中,Weibull分布的拟合回归直线比正态分布和对数正态分布的拟合回归直线精度更高。
3)在实际工程中,与正态分布相比,使用Weibull分布模型来拟合穿刺C/C复合材料的压缩强度分布更加准确。
2.2 拟合优度分析
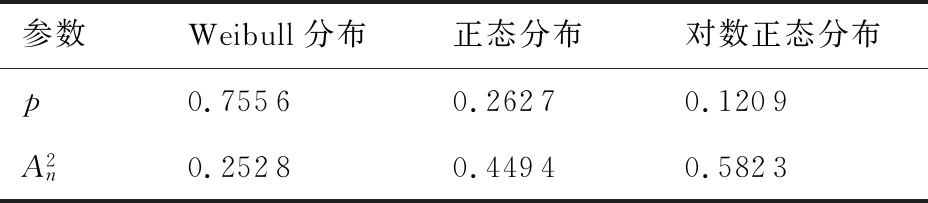
为进一步验证Weibull分布为穿刺C/C复合材料压缩强度分布的最优拟合,本文分别采用K-S检验、A-D检验[15]以及极大似然准则进行拟合优度分析[8]。
2.2.1 K-S检验
K-S检验通过计算拟合失效概率与试验所得中位秩之间的距离来检验拟合分布的精确度,其统计量表达式为
(7)
式中:DN为Kolmogorov距离;Ft(Si)为通过中位秩法计算所得材料在应力达到Si时的失效概率;F(Si)为材料在应力达到Si时的失效概率理论值。
对于选定的显著性水平α,当样本数为30时,存在相应的临界值D30,α,当拟合强度分布的DN值小于临界值D30,α时,样本数据服从所选强度分布模型,DN值越小,表示所选强度分布模型拟合精度越高。工程上显著性水平α常取为0.05或0.1,本文所取的显著性水平为0.05,K-S检验结果由表6给出。
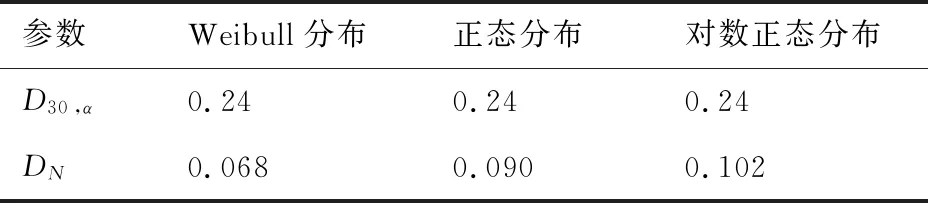
表6 K-S检验结果Table 6 K-S test results
分析表6中Weibull分布、正态分布和对数正态分布的K-S检验DN值可知:上述3种强度分布模型的DN值均小于临界值D30,α,说明上述3种强度分布模型均可用以表征穿刺C/C复合材料的压缩强度分布;且上述3种强度分布模型中,Weibull分布模型的DN值为0.068,明显小于正态分布的DN值(0.090)和对数正态分布的DN值(0.102),即表示Weibull分布对于穿刺C/C复合材料压缩强度分布的拟合优度最高。
2.2.2 A-D检验
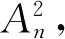
ln(1-F(Xn+1-i))]
(8)
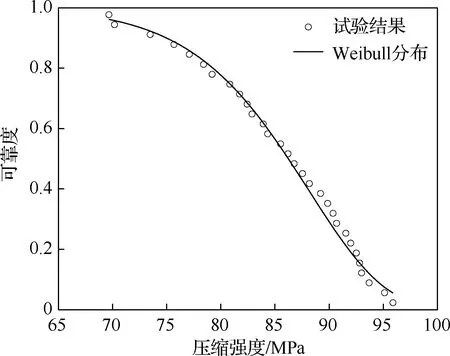
式中:{X1 表7 A-D检验结果Table 7 A-D test results 2.2.3 极大似然检验 除上述K-S检验与A-D检验外,极大似然准则也是拟合优度检验常用的一种方法。与K-S检验、A-D检验不同,根据极大似然准则检验分布模型拟合优度时,其统计量无临界值,记极大似然准则检验统计量为T,根据Cox提出的极大似然准则计算公式[21],统计量T表达式为 (9) 式中:F(Si)、G(Si)分别为所选进行拟合优度比较的两种分布模型的累积概率分布函数。当检验结果T值大于0时,则F(Si)所表示的分布模型拟合精确度更高,反之,T值小于0则说明G(Si)所代表的分布模型拟合精度更高。本文由于需要检验Weibull分布、正态分布和对数正态分布3种分布模型,依据极大似然准则分析拟合优度时需进行多次统计量计算,为表达方便,分别将Weibull分布和正态分布的极大似然准则检验统计量记为T1,Weibull分布和对数正态分布的极大似然准则检验统计量记为T2,正态分布和对数正态分布的极大似然准则检验统计量记为T3,表达式分别为 (10) (11) (12) 根据式(10)~式(12)得到的检验结果如表8所示。 表8 极大似然准则检验结果Table 8 Results of maximum likelihood criterion test 分析表8可知,T1、T2、T3的值均大于0,说明,相较于正态分布与对数正态分布模型,Weibull分布模型对穿刺C/C复合材料压缩强度的拟合度更优。这一结论很好地符合了K-S检验和A-D检验所得出的结论。由此可以确定,Weibull分布可以更好地表征穿刺C/C复合材料的压缩强度分布。 随着工程设计水平的提高,采用绝对化的安全系数来评价材料的可靠性已不能完全满足工程结构对性能的卓越追求,采用统计的方法引入失效概率指标表征材料的可靠性显得十分必要[1]。 分别采用Weibull分布、正态分布和对数正态分布模型,通过线性回归方法计算穿刺C/C复合材料强度的失效概率函数,试验样本的失效概率采用中位秩方法[22]得到,即 (13) 式中:i为当强度由小到大排序后强度Si所对应的序列号;样本总数n=30。失效概率模型中的参数估计值如表5所示。将参数估计值分别代入相应的失效概率计算模型公式中即可得到材料的失效概率函数。图3给出了采用中位秩估计的试验失效概率与Weibull分布、正态分布和对数正态分布模型计算得到的失效概率的对比。 由图3分析可知:3种分布模型所预测的穿刺C/C复合材料压缩强度失效概率曲线均与试验失效概率结果较为接近。为了更直观地体现3种分布所对应失效概率计算模型的拟合精确度,分别计算其平均相对误差,即 (14) 式中:Fi(Si)为拟合所得强度失效概率;Ft(Si)为试验所得强度失效概率。 Weibull分布、正态分布和对数正态分布所对应的失效概率计算模型的平均相对误差分别7.21%、9.98%、12.35%。由此可知,Weibull分布所对应的失效概率计算模型精度更高,与2.2 节结论一致,故本文取Weibull分布模型计算穿刺C/C复合材料的压缩可靠度,计算公式为 R(S)=1-F(S) (15) 式中:R(S)为穿刺C/C复合材料的压缩可靠度;F(S)为对应于Weibull分布的材料失效概率,表达式由表4给出。 根据式(15)得到的穿刺C/C复合材料压缩强度可靠度曲线如图4所示。 图3 失效概率试验值与模型计算值的比较Fig.3 Comparisons of failure probability test value and model calculated value 图4 穿刺C/C复合材料压缩强度可靠度曲线Fig.4 Compressive strength reliability curve of punctured C/C composites 对于给定的可靠度R,根据表4中Weibull分布的累积概率分布表达式以及式(15)可以得到其对应的可靠强度计算式为 (16) 将表5给出的Weibull分布的拟合结果代入式(16)中,即可得到穿刺C/C复合材料在不同可靠度下的压缩可靠强度值,在设计对可靠度要求较高的结构时,可将相应可靠度下的可靠强度值作为设计参考值。 本文通过穿刺C/C复合材料剪切试验的强度数据,采用残差均值分析了样本尺寸对拟合结果精确度的影响,从而确定选择30个分析样本进行穿刺C/C复合材料压缩强度分析;基于线性回归分析法获得Weibull分布、正态分布和对数正态分布的参数拟合值,通过K-S检验、A-D检验以及极大似然准则求得以上3种分布的拟合精度;最后选择Weibull分布模型获得穿刺C/C复合材料的压缩可靠度,得到结论如下: 1)样本数量的增加可以提高分布模型分析结果的准确性,为保证强度分布和可靠性分析的精度,用于获得穿刺C/C复合材料压缩强度分布的最少样本数量应不少于30。 2)基于Weibull、正态、对数正态分布模型预测穿刺C/C复合材料压缩失效概率曲线与试验概率结果均较为吻合,3种分布所对应失效概率计算模型的平均相对误差最大为12.35%,Weibull分布模型对于穿刺C/C复合材料压缩强度分布的拟合优度最高。 3)对于轻量化和可靠性要求的结构,应引入失效概率指标表征材料的可靠性,在设计此类结构时,应参考不同可靠度所对应的材料的可靠强度值。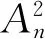


3 可靠性评估

4 结 论

