利用等效法求解竖直平面内的圆周运动分析

柏东宽

摘 要：文章主要阐述高中物理教学中最常用的等效法在竖直平面内的圆周运动中的运用，从基本模型的介绍到模型的深入应用，深入浅出的介绍这种方法在高中物理教学中的应用。

关键词：等效法；圆周运动；竖直平面

等效法在高中物理学科解决问题中最重要的一种科学思维方法之一，等效方法的实质是相互替代的效果相同，等效方法的结果，可以使复杂问题变成简单问题，使感性认识上升到理性认识。在中学物理中合力和分力，合运动和分运动，平均速度，重心，交流电的平均值物理概念均是根据等效方法引入的。本文就质点在竖直平面上的圆形轨道上做圆周运动，利用等效法的思想从基本模型和扩展方面做出一些分析研究。

一、基本模型

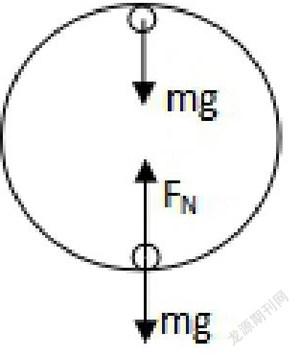
物体在圆形轨道中绕中心点作变速圆周运动，由于轨道只能提供弹力，质点在最高点所受的合力不能为零，合力的最小值是物体的重力，在最低点受重力和弹力，合力提供向心力，所以在最高点：（1）质点过最高点的临界条件：质点达最高点时轨道对物体的弹力刚好为零，质点在最高点的向心力全部由物体的重力来提供，这时有FN+mg=mv2/R，当FN=0时v最小，是小球通过最高点的最小速度叫临界速度；（2）质点能通过最高点的条件是 。在最低点：（1）质点在最低点合力提供向心力FN-mg=mv2/R；（2）质点能通过最高点的条件是v≥0。（3）要做完整的圆周运动mg·2R=mv2/2-mvmin2/2，则过最低点的速度 。

二、带点粒子在电场中的运动

例一、（2013年全国二卷）如图，匀强电场中有一半径为r的光滑绝缘圆轨道，轨道平面与电场方向平行。a、b为轨道直径的两端，该直径与电场方向平行。一电荷量为q（q> 0）的质点沿轨道内侧运动，经过a点和b点时对轨道压力的大小分别为Na和Nb。不计重力，求电场强度的大小E、质点经过a点和b点时的动能。

分析：带电粒子在电场中可以等效为在重力场中，本题把电场力等效为重力，在顺时针旋转90度，就完全可以参照基本模型来处理。

a点即为等效最高点，由基本模型Na+mg=mva2/R

b点即为等效最低点，由基本模型Nb-mg=mvb2/R

a到b，由动能定理qE·2R=mvb2/2-mva2/2

本题利用等效法来处理可以快速的解决问题，只要把模型理解透彻会很快的处理完成，由于本文只是针对知识进行讲解，后续解答就不详细赘述，

三、带电粒子在重力场和电场中的运动

例二、如图所示，在竖直平面内固定的圆形绝缘轨道的圆心为O、半径为R、内壁光滑.该区间存在方向水平向右的匀强电场，一质量为m、带电的小球恰好能在轨道内侧做完整的圆周运动，经过P点时速度最大，O、P连线与竖直方向的夹角θ=60°，重力加速度为g.求：

（1）小球所受到的静电力的大小；

（2）小球对圆轨道的压力最大值是多少？

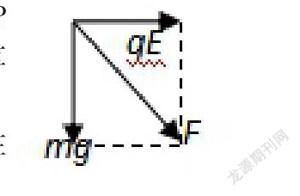
分析：本题把电场和重力场等效为一个场，即把电场力和重力等效为一个力F，如右图。P点速度最快，即P点即为等效最低点，由P点受的场力可以轻松算出静电力F电=qE=mgtanθ，则等效力F=mg/cosθ

P点速度最快，即P点即为等效最低点，在等效最低点有：Np-F=mvp2/R

在圆上沿直径方向上P点对称的点为等效最高点，本题中有关键词“恰好”，即在等效最高点就为等效力F提供向心力即：F=mvo2/R

在等效最高点和等效最低点之间用动能定理，即：F·2R=mvp2/2-mvo2/2

由等效思想我们知道，对圆轨道的最大支持力就是等效最低点的支持力，由牛顿第三定律知，最大压力大小即为NP，综合上述五个公式既可求出。

例三、（2018年全国卷三）如图，在竖直平面内，一半径为R的光滑圆弧轨道ABC和水平轨道PA在A点相切。BC为圆弧轨道的直径。O为圆心，OA和OB之间的夹角为α，sinα=3/5，一质量为m的小球沿水平轨道向右运动，经A点沿圆弧轨道通过C点，落至水平轨道；在整个过程中，除受到重力及轨道作用力外，小球还一直受到一水平恒力的作用，已知小球在C点所受合力的方向指向圆心，且此时小球对轨道的压力恰好为零。重力加速度大小为g。求：

（1）水平恒力的大小和小球到达C点时速度的大小；

（2）小球到达A点时动量的大小；

（3）小球从C点落至水平轨道所用的时间。

分析：本題把可以利用例二的思想，把电场力换成水平恒力即可，即把水平恒力和重力等效为一个力F，如右图，由题目所给的信息，“在C点所受合力的方向指向圆心，且此时小球对轨道的压力恰好为零”，即C点为等效最高点，即水平恒力F1=mgtanθ，则等效力F=mg/cosθ，由此C点的速度也可以快速求出，即F=mvc2/R。

若本题要求求解B点的速度，那就直接用上面的规律就能解出，由于本文只是针对圆周运动进行讲解，后续解答就不详细赘述。

四、总结

等效法求解竖直平面内的圆周运动，最主要的就是找等效最高点和等效最低点，找到以后利用圆周运动知识进行求解，可以快速处理这类题型。

参考文献

[1]闫俊仁.竖直平面内圆周运动的临界问题归纳[J].高中数理化.2005（01）

[2]韩友庆. “等效替代法”在高中物理中的妙用.科学大众·科学教育.2011（09）