构造法在高中数学解题中的有效应用

唐吉忠

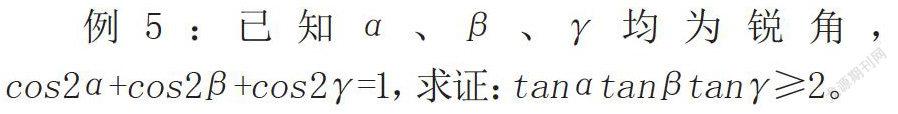
【摘 要】随着新课改不断深入，对高中生的能力也提出了越来越高的要求。因此，高中数学教师除了要针对学生进行数学题训练，还应该积极转变他们的思维，也就是运用一类问题的性质来解决另一类问题。其中，构造法就能够将“未知”量转化成“已知”量，从而不仅有助于学生解决数学问题，而且还培养了他们的观察、分析和创造能力。基于此，本文重点分析了构造法在高中数学解题中的有效应用。

【关键词】构造法;高中数学解题;应用

【中图分类号】G633.6  【文献标识码】A  【文章编号】1671-8437（2019）28-0156-02

1   构造方程（组）

方程主要用来表示两个存在相等关系的数学式，是一个包含未知数的等式，二者之间常常使用等号“=”连接。方程无须以逆向思维进行思考，可以直接列出含有未知数的等式。

方程构造法是高中数学解题中的一种常用方法。另外，方程还是高中数学中的一个重要解题思想，往往能夠同函数相结合，按照问题条件中的数量关系来构建等量方程。然后，再分析此方程中的未知数关系，并运用已知数据进行相应转换，从根本上处理抽象问题，这不仅充分调动了学生的数学学习积极性，而且还能够大大提高学生的解题质量和速度。除此之外，采用方程构造法进行解题的过程中，还有助于提高高中生的观察和思维

能力。

例1：已知（z-x）2-4（x-y）（y-z）=0，证明x，z，y是等差数列。

解题思路：实际上，证明此道题的方法较多。其中，构造法既是一种最简便的解题方法，同时还是学生比较喜欢采用的一种方法。当他们发现等式右边为0时，较易将其同一元二次方程中判定根的方法相结合。因此，学生可以列出一个关于（z-x）2-4（x-y）（y-z）作为判别式的方程，这一方程是（x-y）t2+（z-x）t+（y-z）=0，接着，列出Δ=（z-x）2-4（x-y）（y-z）=0，因此，构建出的方程含有一对相等实根。由于（x-y）+（z-x）+（y-z）=0，因此，两

个实根均是t=1。按照韦达定理可以得出，t2=，从而得出了2y=z+x，因此，x，z，y为等差数列。

例2：已知a，b，c是实数，假设（a+c）（a+b+c）<0，求证：（b-c）2>4a（a+b+c）。

解题思路：根据需要证明的不等式可以联想到b2-4ac这个一元二次方程根的判别式，从而构建出f（x）=ax2+（b-c）x+（a+b+c），因此，只需证明方程f（x）=0有两根，或f（x）与x轴相交就可以。当a=0时，根据已知条件可以得出b≠c，相反，要是b=c，c（b+c）<0<=>2b2<0不成立。当a≠0时，假定f（x）=ax2+（b-c）x+（a+b+c），由于f（0）=a+b+c，f（-1）=2（a+c），加之（a+c）（a+b+c）<0，因此，f（0）·f（-1）<0，因此，f（x）图像与x轴相交，最后得出（b-c）2>4a（a+b+c）。

由此可见，方程构造法在高中数学解题过程中的应用，既能够减少数学题的难度，同时还提升了学生的思维能力以及学习效率。

2   构造函数

在高中数学解题教学的过程中，教师的主要教学任务就是培养学生的解题思想。事实上，数学问题均包含了函数思想。因此，在解决代数和几何等数学问题的过程中，要是能够把有关问题重新构造成函数问题，就可以节约大量解题时间，既培养了学生的数学思维和创新能力，同时还激发出了他们的数学学习热情。

例3：在x∈（0，+∞）这区间内，证明x>ln（1+x）。

解题思路：设g（x）=x-ln（1+x）。由x∈（0，+∞），因此，g'（x）=1-，而且在此区间内，x+1一直比1大，因

此，一直比1小，为此，g'（x）一直比0大。还由于g（x）在x=0处连续，因此，在（0，+∞）这一区间内，g（x）为增函数。从而得出g（x）>g（0）=0。x-ln（1+x）>0，最终得出结论：x>ln（1+x）。

例4：已知函数f（x）的定义域是R，f（0）=2，x∈任意R，f（x）+f’（x）>1，求证：不等式ex·f（x）>ex+1的解集。

解题思路：首先，采用构造法构造函数g（x）=ex·f（x）-ex，然后再按照问题条件，通过移项合并，得出g’（x）=ex·（f（x）+f’（x））-ex>0，所以，g（x）是R上的增函数。另外，根据已知条件还能够得出，g（0）=e0·f（0）-e0=1，因此，g（x）>g（0），最后得出结论x>0，从而求得x的解集是{x∈R，x>0}。

采用函数构造法解决数学问题不仅清晰明了，而且还简单易懂，除此之外，还具有较强的灵活性。因此，对其加以应用时，一定要有针对性地进行构造，紧扣解题

目标[1]。

3   构造图形

大量高中数学教学实践表明，大多数高中生都不喜欢学习理论知识，这主要是由于数学理论比较抽象难懂，从而限制了学生的思维。然而，让学生结合问题条件将相应的图形画出来，却有助于他们深入理解题干，还能够充分调动起他们的学习积极性。由于图像能够使学生产生一种直观体验，因此图形构造法是解决数学问题的一种有效方法[2]。

例5：已知α、β、γ均为锐角，cos2α+cos2β+cos2γ=1，求证：tanαtanβtanγ≥2。

解题思路：高中生看到三角函数就较易将其同长方体中的对角线和棱组成角的有关性质相结合，基于此，高中生可以构建出相应的三角形。并分别设长方体的长、宽、高为a、b与c，并且在点B相交的三条棱与对角线BD1间的夹角分别为α、β和γ。所以，可以将之前的三角不等式变换成适当的代数不等式，最后得出结论：tanαtanβtanγ≥2。

4   结语

综上所述，高中生在学习数学知识的过程中，倘若根据思维定式难以探究解题思路与方法时，可以针对不同的数学问题采用相应的构造法，以此来培养学生的创新思维和创造意识，从而有助于提高他们现有的解题能力。其中，函数、方程、图形和模型构造法均属于高中数学解题过程中的常用方法，这些构造法能够帮助学生探究出合适的解题思路与方法。由此可见，针对构造法在高中数学解题中的运用展开深入研究显得十分必要。

【参考文献】

[1]冯旭明.浅谈构造法在高中数学解题中的应用[J].数理化解题研究，2017（7）.

[2]何忆捷，熊斌.中学数学中构造法解题的思维模式及教育价值[J].数学教育学报，2018（2）.