高考复习中提升逻辑推理素养的研究

梁佶

摘 要：高中数学课程标准特别关注学生数学核心素养的形成和发展，逻辑推理是数学核心素养的重要组成部分之一，在近几年全国高考数学试题中对逻辑推理素养的考查贯穿全卷。本文结合多年的高三一线数学教学实践，从逻辑推理素养的界定、分类入手，初步研究了高考复习中提升逻辑推理素养的策略。

关键词：逻辑推理、高考复习、数学核心素养

1.问题提出

进入高考复习阶段，由于复习内容繁多，教学任务重，很多教师在复习中进行“填鸭式”的教学，让学生被动接受知识。在这种情况下，很多学生不会独立分析与思考，不会独立推理论证。因此，在高考复习中要提升逻辑推理素养，从千变万化的试题中把握解题的规律和方法。

普通高中数学课程标准的基本理念是以学生发展为本，落实立德树人为根本任务，提升数学核心素养。逻辑推理素养是高中数学素养的重要组成部分。本文结合多年高三一线教学实践，研究高考复习中提升学生数学逻辑推理素养的策略。

2.逻辑推理素养的认识

2.1逻辑推理素养的界定

逻辑推理是指从一些事实和命题依据推出其它命题。逻辑推理是得到数学结论，构建数学体系的重要方式，是数学严谨性的保证，是人们在数学活动中进行交流的基本思想品质。其主要表现为：掌握推理基本形式和规则，发现问题和提出命题，探索和表达论证过程，有逻辑地表达和交流。

2.2逻辑推理的分类

一类是合情推理，包过归纳推理和类比推理。例如等差数列与等比数列的类比、平面与立体的类比等。另一类是演绎推理，这种推理的一般推理模式是“三段论”，包过

大前提、小前提、和结论。数学中大部分的推理是以演绎推理为主。

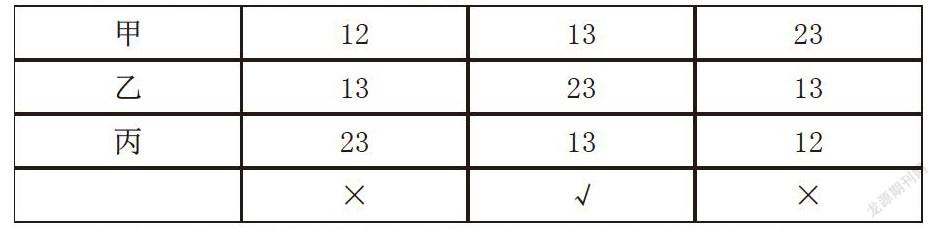
例1（2016年全国Ⅰ卷，理）若a>b>1，0

A.ac

分析：本题可以用指数函数和对数函数的单调性进行解题，也可用特例法，令

a=4，b=2，c=即可排除选项A、B、D，这两种解法都是从一般到特殊的推理，即演绎推理。

3.提升逻辑推理素养的策略

3.1在考点复习中提升逻辑推理的基础

在高考复习中要让学生弄清楚公式、概念定理产生的过程和相互之间的关系，并构建知识

网络，熟记于心，打好逻辑推理的基础。以下是一次模拟考试中一位学生的答题实录：

例2如图，三棱柱ABC-A1B1C1中，CA=CB，AB=AA1，∠BAA1=60°;平面ABC平面ABB1A1，E为线段AB的中点。证明A1E⊥平面ABC.

错解：∵AB=AA1，∠BAA1=60°，∴△BAA1是正三角形，E为线段AB的中点，∴A1E⊥AB，

∵平面ABC平面ABB1A1AC平面ABC，A1E平面平面ABB1A1

∴A1E⊥AC，又ABAC=A∴A1E⊥平面ABC.

该生在推理论证过程中，由“平面ABC平面ABB1A1，AC平面ABC，A1E平面平面ABB1A1”推出“A1E⊥AC”是错误的，因为两個平面垂直，但这两个平面内的直线不一定相互垂直。这是由于对立体几何中的有关定理和概念混淆不清造成的。

3.2在试题评讲中提升逻辑推理的能力

建构主义理论认为：学习不是由老师把知识简单地传递给学生，而是由学生自己建构知识

的过程。新课程标准提倡以发展学生数学核心素养为导向，提倡独立思考、自主学习、合作交流等多种学习方式。在高考复习中要多留一些时间让学生自主探究和推理论证，切忌包办代替。

例3（2010全国Ⅰ卷，理）已知函数f（x）=|lgx|.若0<a<b，且f（a）=f（b），则a+2b的取值范围是（A）

A.B.C.D.

教法一：教师给出题目，学生思考，老师讲解学生听或师生一起解答。在这个过程中学生虽然参与了教学活动，但学生的思维是被动的。

教法二：教师出示题目，学生思考、讨论、探究，老师巡视在必要时进行引导提示，最后学生得出以下几种解题思路和方法：

方法1：特例法

令a+2b=3，则b=，结合0<a<b，得到.

由f（a）=f（b）得|lga|=|lg|，∴a=1或2，与矛盾，可排除A、B、D选项。

方法2：要求a+2b的取值范围，必须要需找出a与b的关系，将a+2b用a或b来表示，用函数的方法求出。

点评：方法2中在求a+的取值范围时有的学生用基本不等式来求，但忽略了等号成立的条件，导致选A答案。整个过程能让学生自主探究和主动思考，让学生感受到主动思维成功的喜悦和数学的趣味性，从而更加主动参与数学思维活动，进一步提升逻辑推理能力。

3.3在练习中提升逻辑推理的严谨性

数学逻辑推理必须要有严谨性，否则推理过程就会出现错误。平时要养成严谨推理的习惯。

认真审题，精确运算，推理论证要步步有据可依。例如立体几何中用综合法证明垂直与平行关系时很容易漏写定理的某个条件，而且书写的思路可能比较混乱乱。可用“逆推法”寻找证明的思路，再书写证明的过程。

例4（2009江西卷，理）在四棱锥P-ABCD中，底面ABCD是矩形，PA⊥平面ABCD，PA=AD=4，AB=2.以AC的中点O为球心、AC为直径的球面PD于点M，交PC于点N.

求证：平面ABM⊥平面PCD;

分析：

通过上述分析之后，就能找到清晰的证明思路，从而保证推理论证过程的严谨性。

3.4在总结反思中掌握逻辑推理的方法

高考复习中要完成一定量的题目是必须的，但也不能搞“题海战术”，否则会给学习带来负担，复习的效果也不好。在解题之后要进行总结反思，从中掌握解题的思路和推理论证的方法，力争在解决一个问题后能掌握一类问题的解决方法。

例5（2016全国Ⅱ卷，理）有三张卡片，分别写有1和2，1和3，2和3.甲，乙，丙三人各取走一张卡片，甲看了乙的卡片后说：“我与乙的卡片上相同的数字不是2”，乙看了丙的卡片后说：“我与丙的卡片上相同的数字不是1”，丙说：“我的卡片上的数字之和不是5”，则甲的卡片上的数字是.

解：根据题设列表分析如下：

甲 12 13 23

乙 13 23 13

丙 23 13 12

× √ ×

由表可知只有甲卡片上的数字是1和3符合题意。

点评：对于这类逻辑推理型的题目，可以通过列表分析，便于推理。

总之，在高考复习中教师要改变教学观念和教学模式，切忌以练习代替复习。教学中既要

注重基础知识的教学，也要注重学生数学核心素养尤其是逻辑推理素养的提升，这样才能有效地提高高考复习的效率。

参考文献

[1]教育部，普通高中数学课程标准（2017年版）

[2]罗增儒，从数学知识的传授到数学素养的生成[J].中学教学参考：上旬2016（7）;2-6

[3]许钦彪，教之目的是学，学之目的是思[J].中学教学参考：上旬2016（8）：18-20

[4]林运来、杜锟，注重核心素养，引领数学改革[J].中学数学教学参考：上旬2016

[5]罗增儒，高考复习要抓准方向[J].中学数学教学参考：上旬2016（10）：2-7