一类平衡的广义割圆序列的二进制复杂度研究*
赵春娥,孙玉花,闫统江
1.中国石油大学(华东)理学院,青岛266580
2.应用数学福建省高校重点实验室(莆田学院),莆田351100
3.齐鲁工业大学(山东省科学院),山东省计算中心(国家超级计算济南中心),山东省计算机网络重点实验室,济南250014
1 引言
具有良好统计特性的伪随机序列被广泛应用于密码学和通信系统.二进制复杂度是衡量序列伪随机性质的一个重要指标,Klapper 在1997年提出二进制复杂度的概念[1],并指出任何一个二元序列都可以由带进位的反馈移位寄存器(FCSR)生成,他将二进制复杂度定义为生成序列的最短FCSR 的级数.同时Klapper 又给出针对二进制复杂度的有理逼近算法(RAA),该算法要求安全的密钥流序列的二进制复杂度不小于其周期的一半,所以计算密钥流序列的二进制复杂度是一项重要的研究课题.此外,Klapper还指出具有质数周期的m-序列具有极大二进制复杂度.2010年,Tian和Qi 证明了所有二元m-序列的二进制复杂度都是极大的[2].2014年,Xiong 等人提出了一种利用循环矩阵来计算二元序列的二进制复杂度的新方法,并用此方法证明了所有已知的具有理想2 值自相关的序列具有极大的二进制复杂度[3].随后,胡红钢用另一种简捷的方法证明了这一结论[4].此后这两种方法被广泛应用在序列的二进制复杂度求解中.例如,Xiong 等人证明了具有最优自相关的Legendre 序列、Ding-Helleseth-Lam 序列和另外两类基于交织结构的序列也具有极大的二进制复杂度[3,5],曾祥勇、孙玉花、Winterhof 等人分别研究了几类广义割圆序列的二进制复杂度[6–8].本文研究一类2 阶的pq周期的Whiteman 广义割圆序列的二进制复杂度,这类序列由Ding和Helleseth 给出[9],具有最优的平衡性,而白恩健等人则证明了这类序列具有很高的线性复杂度[10].
2 一类Whiteman 广义割圆序列及序列的二进制复杂度定义
设N=pq,其中p,q是互不相同的奇素数,满足p 存在唯一解x.令e=(p−1)(q−1)/2,定义集合 则称它们为ZN上关于素数p和q的2 阶Whiteman 广义割圆类.Whiteman 已经证明[8] 并称4 个交集的元素个数(i,j)=|(Di+1)∩Dj|(其中i=0,1;j=0,1)为相应的广义割圆数,其中Di+1={x+1|x∈Di}.令 该序列由Ding和Helleseth 给出[9],白恩健等人则证明了这类序列具有很高的线性复杂度[10]. 定义1令N是一个正整数是一个周期为N的二元序列,令若 由上面的式(2)可以看出,φ2(s)可通过式(3)求出: 本文研究q=p+4时序列的二进制复杂度,并给出此时序列的二进制复杂度的一个下界.因此,如无特别说明,后文将总假定p和q满足gcd(p−1,q−1)=2,q=p+4,从而此时必有q≡p≡3 mod 4. 引理 1[3]是周期为N的二元序列,A=(aij)N×N是一个N阶矩阵,其中aij=S(j−i)modN,则 (2)如果det(A)=0,则gcdS(2),2N−1gcd(det(A),2N−1). 结合上节式(3)中φ2(s)的表达式和引理1 中的(2)可以看出,如果求出行列式det(A)的值,就能分析出φ2(s)的一个下界.为了计算det(A)的值,需要下面一系列引理. 引理2[11]对于任何一个a∈ZN和B⊆ZN,记aB={ab|b∈B},则有以下性质 (1)对于每一个固定的a∈Di,有aP=P,aQ=Q,且aDj=D(i+j)mod2,其中i,j=0,1. (2)对于每一个固定的a∈P,如果b取遍Di中的每个元素时,则元素ab恰好取到P中每一个元素次,并且aP=P,aQ=R. (3)对于每一个固定的a∈Q,如果b取遍Di中的每个元素时,则元素ab恰好取到Q中每一个元素次,并且aQ=Q,aP=R. 定义2[6]令p,q是满足gcd(p−1,q−1)=2 的两个奇素数,N=pq,Dj如前所述,令是复数域上一个N次本原单位根,则称为基于2 阶割圆类的高斯周期,其中j=0,1. 引理3[6]令gcd(p−1,q−1)=2,p≡3(mod4),q≡3(mod4),ηi是如上定义的基于Di的高斯周期,其中i=0,1,则有 引理4[7]令p≡3 mod 4 为奇素数,记则 引理5令p≡3 mod 4,q≡3 mod 4 为奇素数,若为整数,则 证明:由引理4 知分别互为共轭复数,令而由的值可知因此,四种组合如下必为整数: 把D0,D1进一步划分如下: 则D0=D00∪D01,D1=D10∪D11. 定理1设为式(1)所定义的二元序列,限定p,q是满足gcd(p−1,q−1)=2,q=p+4 的奇素数,则 证明:由引理2,则 (1)a∈R时, 类似地,可以得到 (6)a∈D00时, (7)a∈D01时, (8)a∈D10时, (9)a∈D11时, 定理2设为式(1)所定义二元序列,并限定p,q是满足gcd(p−1,q−1)=2,q=p+4 的奇素数,则 证明:由引理1和定理1 得 注意到p≡q≡3 mod 4,由引理3–4 得 将其代入得 又因为q=p+4,所以 引理6[6]令p和q是互不相同的奇素数,并且N=pq,则且特别地,如果p 定理3设为式(1)所定义的二元序列,并限定p,q是满足gcd(p−1,q−1)=2,q=p+4的奇素数,则的二进制复杂度满足φ2(s)≥pq−p−q−1. 证明:根据定理2 由引理1 的(2),我们需要分析gcd(det(A),2N−1).下面依次分析上述行列式表达式中每一项因子和2N−1 的公因子。 令r是2N−1 的任意一个素因子,Ordr(2)是模r的乘法阶,则2Ordr(2)≡1 modr,因此r|2Ordr(2)−1,又由r|2N−1,可得Ordr(2)|N.特别地,对于N=p(p+4),则Ordr(2)=p(p+4),p或p+4.下面我们将分三种情况来证明gcd(det(A),2N−1)≤(2p−1)(2p+4−1). • Ordr(2)=p(p+4).根据费马小定理,r|2r−1−1,因此Ordr(2)≤r−1.由于Ordr(2)=p(p+4),所以,我们有p(p+4)≤r−1,即r≥p(p+4)+1,而式(5)中前三个因式都满足因此前三项都与2N−1 互素,而对于最后一个因子项来说,由费马小定理可知Ordr(2)|r−1,那么有pq|r−1,令r=kpq+ 1.若即pq(pq+2p+2q−10)+4q+9=16ktpq+16t.若16t • Ordr(2)=p.由于Ordr(2)≤r−1,因此p≤r−1,所以因此由于2p≡1 modr,因此r|2p−1.由于gcd(r,p+4)=1,根据引理6,因此gcd(det(A),2N−1)|2p−1. • Ordr(2)=p+4.显然r|2p+4−1.由引理6,1.因此gcd(det(A),2N−1)|2p+4−1. 综合三种情况,可知gcd(det(A),2N−1)|(2p−1)(2p+4−1),且1.这说明gcd(det(A),2N−1)≤(2p−1)(2p+4−1),由引理1 最后,根据二进制复杂度的定义,我们得到 本文对一类平衡的广义分圆序列的二进制复杂度进行研究,此类序列之前已经被证明了具有很高的线性复杂度足以抵抗线性攻击.本文的结果表明此序列同样具有较高的二进制复杂度,也足以抵抗针对带进位的线性反馈移位寄存器(FCSR)所提出的有理逼近算法(RAA)的攻击.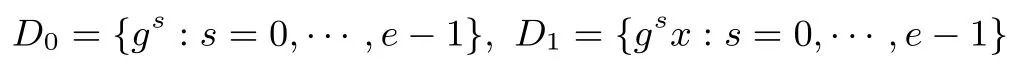
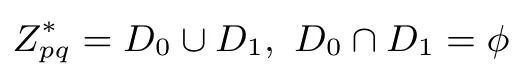
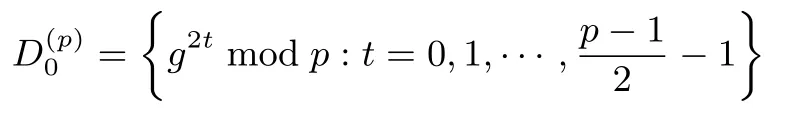


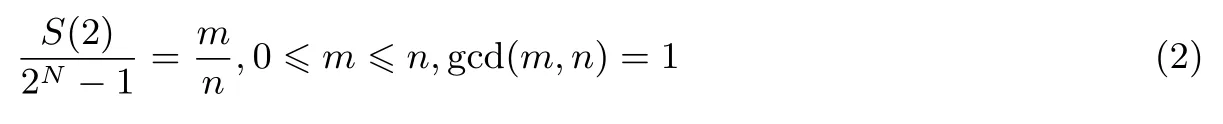

3 一类Whiteman 广义割圆序列的二进制复杂度
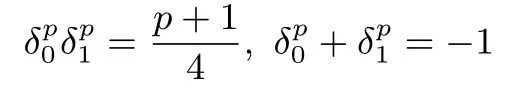
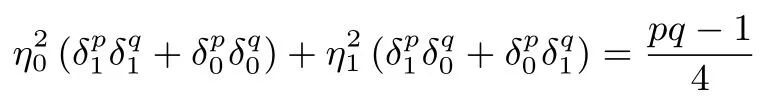

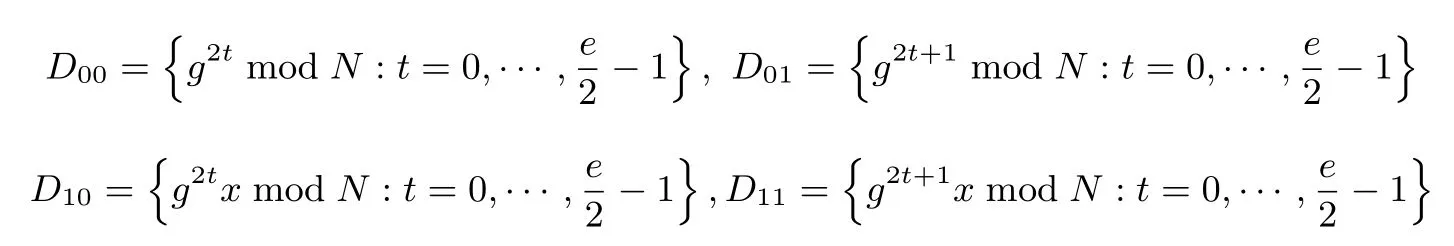

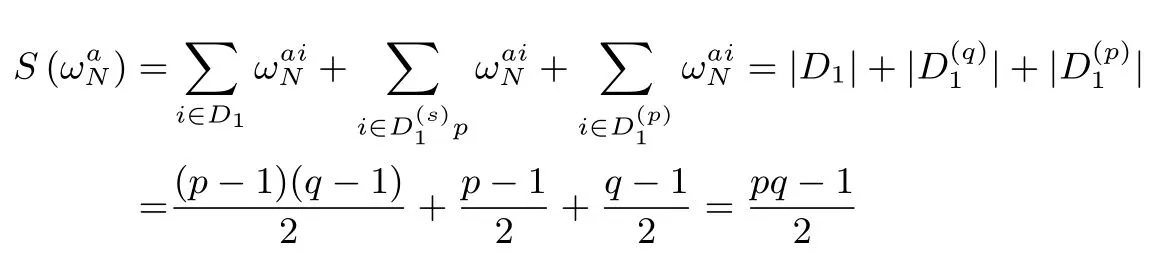

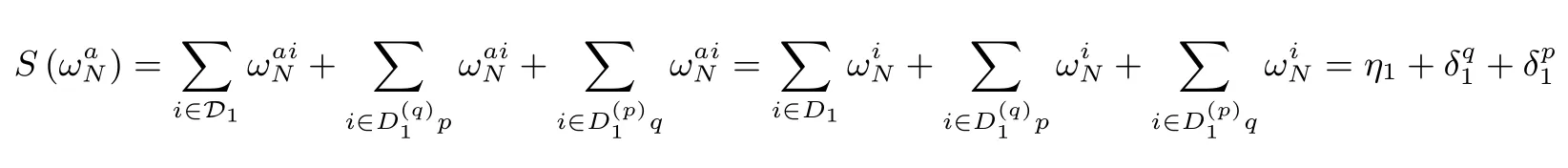
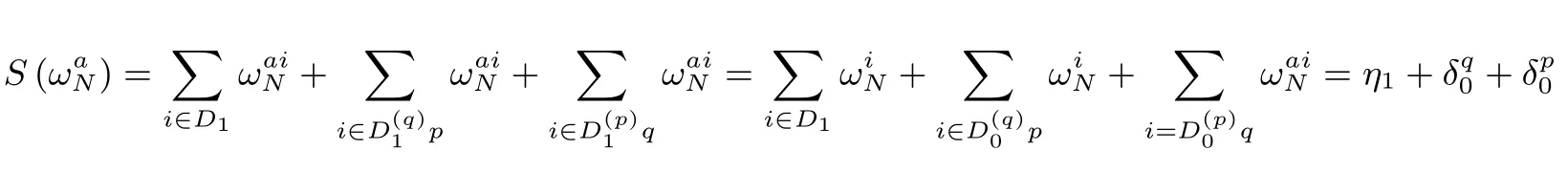
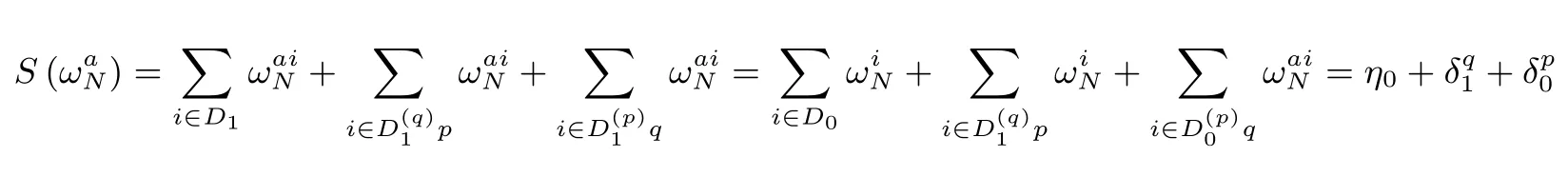
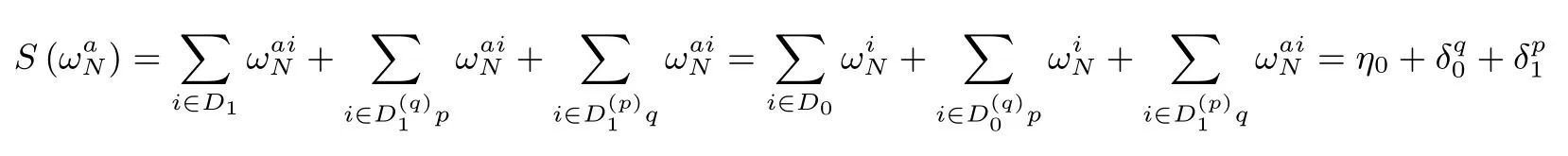

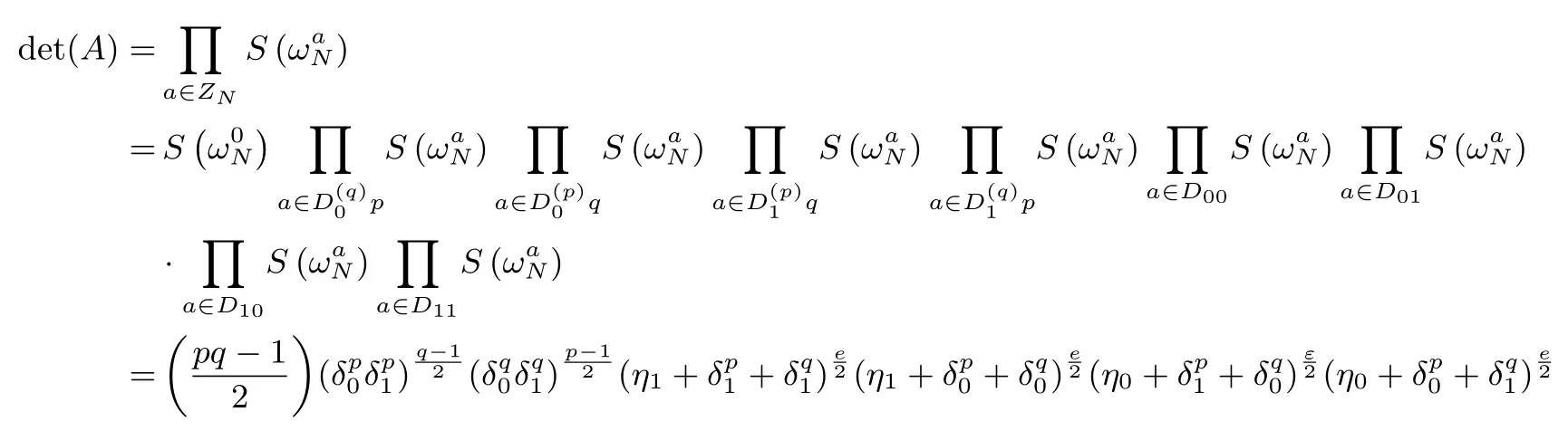

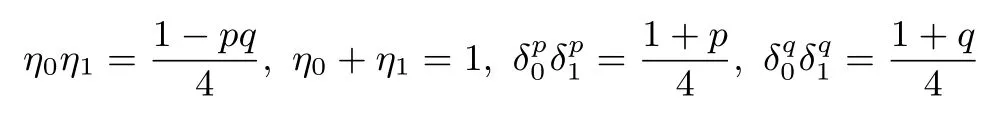
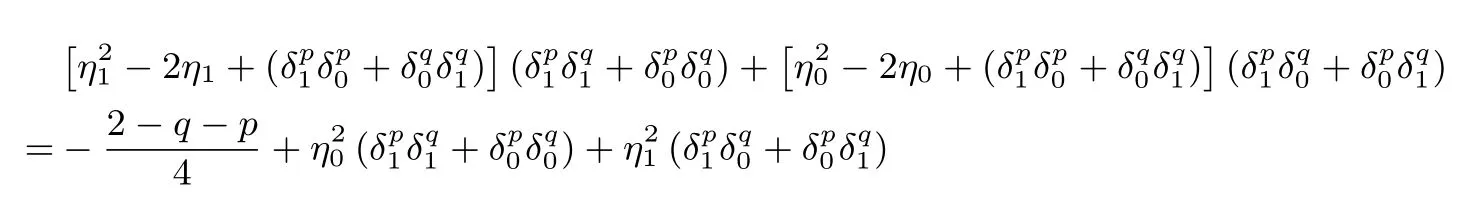
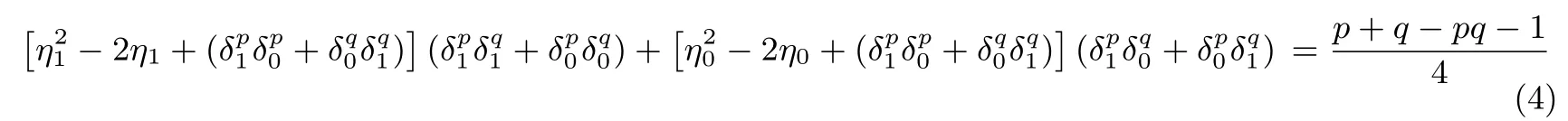
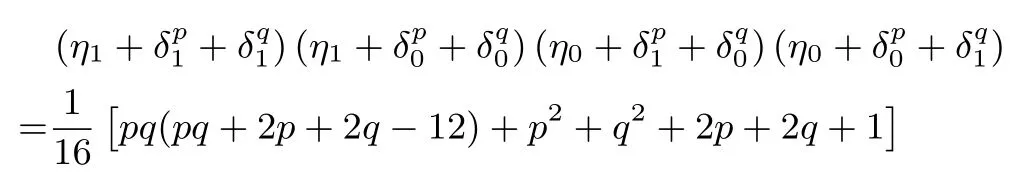
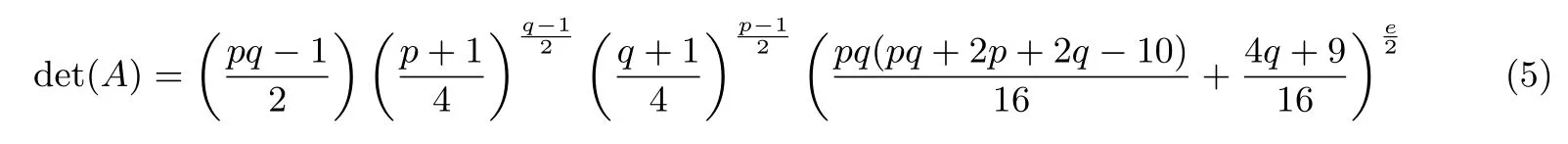
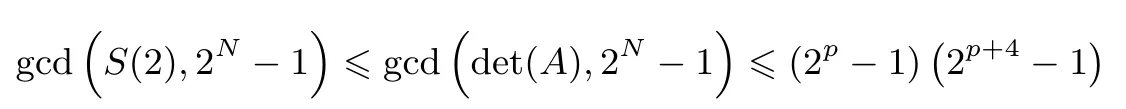
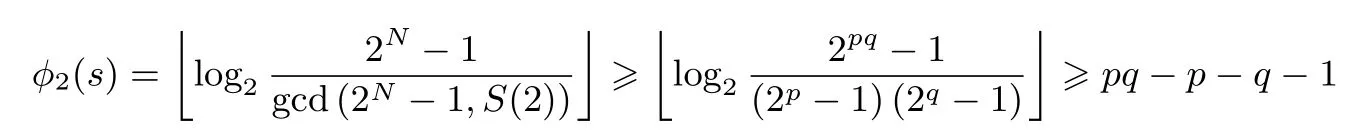
4 结论

