快速素数生成方法综述
李 峰,龚宗跃,2,雷翻翻,顾 申,高 鹏
1.大唐微电子技术有限公司,北京100094
2.北京航空航天大学,北京100191
3.北华大学 计算机科学技术学院,吉林132013
1 引言
素数在很多密码算法和协议中都有使用,有些算法的安全性完全取决于素数的保密性[1–4],如RSA[1]中,取素数p和q,计算参数N=pq及私钥d=e−1modφ(N)(e为选定的公钥参数); 算法的理论安全性基于大数N分解的困难性,实际的安全性基于素数p和q的保密性及所使用p,q的安全性.
素数生成对很多密码算法是至关重要的,而由于大素数分布的稀疏性,素数生成是一个很耗时的过程.因此,研究快速高效的素数生成方法是有必要的.
各种素数生成方法的算法流程虽然不完全一致,但是整体思路都是一样的,流程如图1所示.
图1中可看到素数生成分为3 步,分别为选取初值、增量变换、素性检测,对于快速素数生成算法的研究也从这三步着手进行.
初值p的选取有两类主要算法,一类是直接选取随机奇数,另一类是选取与小素数乘积互素的数.文献[5]提到,确保一个随机奇数不能被3、5和7 整除,即可在素数检测前排除54% 的奇数; 确保随机奇数与小于100 的素数均互素即可排除76% 的奇数.
进行增量变换时,增量函数f的选取是一个关键点,不同算法对f的选取不同,可以每次给初值加2、每次加一个素数或经过一个复杂的函数变换.
素性检测是所有素数生成算法必不可少的一个环节,有两大类检测方法,一类是可证明素数检测,另一类是概率素数检测.实践中概率素数检测算法使用更为广泛,经概率素数检测算法通过的素数有时也被称为“工业级素数”.
2 生成与小素数乘积互素数的算法
本节主要介绍几种生成与小素数乘积互素数的算法及其相关理论基础.素数生成算法中初值的生成常用这类算法.
2.1 查表法
定理1(中国剩余定理[5])若m1,m2,··· ,mn两两互素且都大于1,a1,a2,··· ,an是任意整数,则存在一个解x满足同余方程组:
其解一定可以写成以下形式:
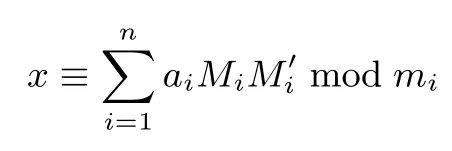
且θi满足同余方程组

则由中国剩余定理可得
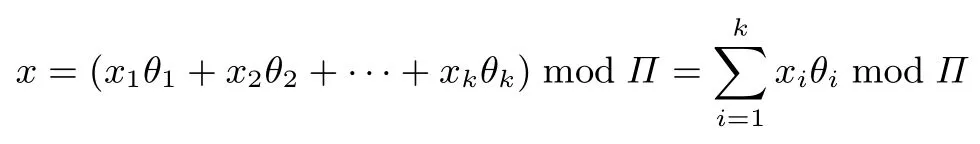
故可得到以下等价条件:
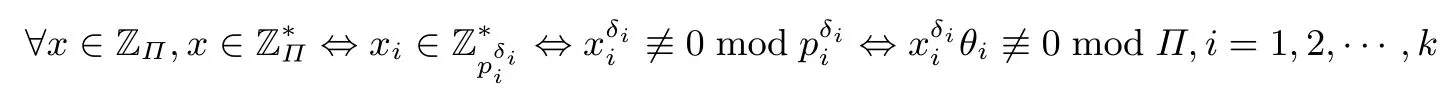
对于一个固定的Π,可以计算得到θi,再选择k个随机数xi满足这样可以得到一个与Π的每个因子都互素的x.因此,可以得到算法1[6].
该算法需要存储预计算得到的θi,因此需要较大的存储空间.实际使用中通常对于选定Π的将θi进行预存,提高算法执行效率.
2.2 模搜索法
定义1(Carmichaelλ函数)对任意整数为素数.λ(N)的定义如下:

其中p为素数.

算法1 查表法Input:Π=∏ki=1pδii Output:与Π 互素的数c 1 预处理:2 计算θi:3 for i=1 to k do()[()−1]4 θi=ΠΠ pδi mod pδi i i pδi i 5 end 6 计算其他参数:t=C ·max(pδi)i ,pδi i 表示pδii 的比特数,C 通常取2.7 主运算:8 c=0,i=1 9 while i≤k do 10 取t 比特的随机数x 11 if xδiθi mod Π=0 then 12 Goto Step 9 13 end 14 c=(c+xθi)mod Π 15 i=i+1 16 end 17 返回c
定理2(Carmichael 定理[7])设a和N都是正整数,且gcd(a,N)=1,则

其中λ(N)是Carmichael 函数.
由定理2易得推论1.
推论1设a和N都是正整数,若有aλ(N)≡1 modN成立,则有gcd(a,N)=1,其中λ(N)是Carmichael 函数.
由推论1,可得算法2.该算法不需要任何预存值,但要多次计算指数为λ(Π)的模幂运算,算法执行效率较低.

算法2 模搜索法Input:Π=∏k i=1pδii Output:与Π 互素的数c 1 取n 比特随机数c,使其满足c < Π 2 while cλ(Π) mod Π=1 do 3 c=c+1 4 end 5 返回c
2.3 改进的模搜索法
定理3令整数k,r∈ZΠ,若gcd(k,r,Π)=1,则有

可以利用定理3对算法2 进行优化,得算法3[8].

算法3 改进的模搜索法Input:Π=∏k i=1pδii ,λ(Π)Output:与Π 互素的数c 1 取随机数c ∈ZΠ 2 U=(1−cλ(Π))mod Π 3 while U=0 do 4 取随机数r ∈ZΠ 5 c=c+rU 6 U=(1−cλ(Π))mod Π 7 end 8 返回c
该算法运算量和算法2基本相当,但循环次数有所减少,从而缩短运算时间.
3 素数生成主算法
本节介绍素数生成中最重要的一个步骤,增量函数f的设计.下文描述中使用T(q)表示对q进行素性检测,当q是素数时返回True,否则返回False.
3.1 原生算法
最原始的生成素数方法就是取一个随机奇数,进行素性检测,如果不是素数则重新取一个随机数,直到找到一个素数.

算法4 原生素数生成算法Input:要生成素数的比特位数n Output:素数q 1 取n 比特随机奇数q 2 while !T(q)do 3 取n 比特随机奇数q 4 end 5 返回q
接下来讨论理论上该算法所需素数检测次数.
定义2(素数分布函数[9])素数分布函数π(x)表示小于或等于x的素数个数,表达式可以写为且p是素数1,其中x是大于1 的正实数.
定理4(素数定理)π(x)是的渐进,即
定义3(Li(x)函数)Li(x)[10]是一个比更好的π(x)的逼近,令x是大于1 的正实数,则


由于公式(2)需计算极限,计算不是很方便,在有限误差范围内,Li(x)可以近似写成

该式与式(1)仅相差一个常数Li(2)≈1.05.
定理5π(x)是Li(x)的渐进,即
根据定理4和定理5,得到算法4生成满n比特随机数时平均素数检测次数的两个近似值,分别为
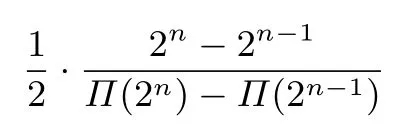
和


表1 算法4平均素数检测次数Table 1 Average prime test times of Algorithm 4
由表1可知算法4所需素数检测的次数较多,生成素数平均时间较长.
3.2 增量素数生成算法
算法4效率较低,算法5对其进行改进.该算法由Jorgen Brandt 等[11]提出并在文献[12]中对其性能进行了全面分析.

算法5 增量素数生成算法Input:要生成素数的比特位数n Output:素数q 1 取n 比特随机奇数q 2 while !T(q)do 3 q=q+2 4 end 5 返回q
由于素数分布的不均匀性,因此从理论上无法计算出该算法平均需要进行的素数检测次数,除非已知了指定范围内所有素数的分布.经过实验分析,该算法平均素数检测次数比算法4略有减少,算法5的另一优势在于能提高素数检测效率,将在4.2节进行讨论.
3.3 改进的增量素数生成算法
对算法5进行两方面改进,一方面取初值q满足gcd(q,Π)=1,其中Π是小素数乘积,通常Π=2×3×5×···×29; 另一方面,迭代过程由q=q+2 改进为q=q+Π,这样可以保证每个q均没有这些小素因子.
详细算法描述见算法6.

算法6 改进的增量素数生成算法Input:要生成素数的比特位数n,前k 个小素数乘积Π=∏ki=1pi Output:素数q 1 取n 比特随机奇数q,使之满足gcd(q,Π)=1 2 while !T(q)do 3 q=q+Π 4 end 5 返回q
与算法5类似,由于素数分布的非均匀性,该算法需要进行的素数检测次数也无法得到理论上的确定值,但可以确定该算法的素数检测次数与参数k直接相关,在一定范围内,k取值越大所需素数检测次数越少.步骤1可使用算法1–3实现.
3.4 M-J 素数生成算法
M-J 素数生成算法由Marc Joye 等在文献[6]中提出.该算法对算法6进行了改进,减少了所需素数检测的次数.
素数生成一般指定一个生成范围[wmin,wmax],在密码算法中一般都是生成固定n比特的素数,通常取wmin=2n−1+1,wmax=2n−1.
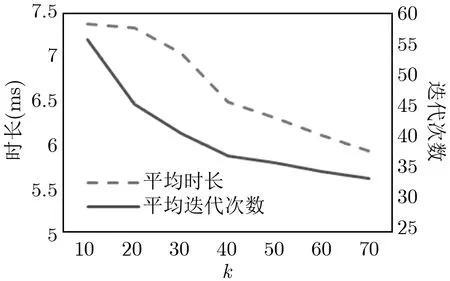
取参数Π满足Π 且使不等式两端的值尽量接近,即 为下文描述方便,记ψ=εmaxΠ,τ=εminΠ.M-J 算法流程见算法7. 算法7 M-J 素数生成算法Input:要生成素数的比特位数n,ψ和τ Output:素数q 1 取随机数c,使c ∈Z∗ψ 2 计算q=c+τ 3 while !T(q)do 4 c=fa(c)5 q=c+τ 6 end 7 返回q Marc Joye 在文献[6]中给出生成n比特素数时算法7的时间复杂度为O(n4/lnn),但未给出完整的证明. 考虑算法实现的效率,可以令步骤4中a=2,即ci=2ci−1modψ,乘2 的运算可以通过左移位快速实现,同时乘2 后的取模运算可以转换为大数减运算,即ci=2ci−1或ci=2ci−1−ψ.由于有限制条件故取a=2时需要限制gcd(ψ,2)=1,则Π中不能包括因子2,εmax为奇数.因为ψ是奇数,所以步骤5得到的候选值qi可能是偶数.当qi为偶数时,给其加Π保证进行素数检测的qi全部为奇数.由此得到算法7的一个特例,流程见算法7A[6]. 算法7A M-J 素数生成算法的特例Input:要生成素数的比特位数n,ψ和τ和Π(不含因子2)Output:素数q 1 取随机奇数c,使c ∈Z∗ψ 2 计算q=c+τ 3 if q mod 2=0 then 4 q=q+Π 5 if !T(q)then 6 c=2c mod ψ 7 Goto Step 2 8 返回q 实际中常使用算法7A,可有效缩短生成素数的时间,提高效率. 给定目标素数范围[wmin,wmax],首先生成算法参数.选一个小数0 <ε≤1(一般取10−2或者10−3),选择小素数的乘积则存在整数t,u,v满足以下条件: (1)1−ε<(uΠ−1)/(wmax−wmin)≤1; (2)vΠ+t≥wmin; (3)(u+v)Π+t−1≤wmax; (4)Π包括尽量多的不同的素因子且Π 根据参数(wmin,wmax,ε)得到参数(Π,t,u,v),即可进行素数生成,见算法8. 令ψ=uΠ,τ=vΠ,取随机数且a=1. 算法8 改进的M-J 素数生成算法Input:t,ψ,τ和a Output:素数q 1 取随机数k ∈Z∗ψ 2 计算q=[(k−t)mod ψ]+t+τ 3 if !T(q)then 4 k=a·k mod ψ 5 Goto Step 2 6 返回q 算法8生成素数实际的分布范围为[vΠ+t,(u+v)Π+t−1]⊆[wmin,wmax],是目标素数范围的一个子集.该子集与目标范围的接近程度由参数ε决定. 该算法可以保证进行素数检测的每一个q均满足gcd(q,Π)=1.该算法通用性较好,输出素数的分布也比算法7更好.文献[8]给出了算法8生成n比特素数时所需素数检测次数为n·ln 2·ϕ(Π)/Π=O(n/lnn). 令u=1,这样一次取值的区间长度就变成了Π−1,为了使取随机数的范围尽可能接近目标范围,将t的取值由固定值改为Π的随机倍数,即t=bΠ,每次取数时b在变化.此外,令a=2,步骤4只需要进行移位和减运算,速度有明显提升;a=2时必须使才能保证成立此时,上述的4 个条件将变成如下形式: (1)1−ε<((bmax−bmin+1)Π−1)/(wmax−wmin)≤1; (2)(v+bmin)Π≥wmin; (3)(v+1+bmax)Π−1≤wmax; (4)Π包括尽量多的不同的素因子且Π 此时就得到算法8的一个特例,算法8A. 算法8A 改进的M-J 素数生成算法的特例Input:Π=∏i pi(pi=2),τ=vΠ,bmin,bmaxOutput:素数q 1 取随机数k ∈Z∗Π 2 取随机数b ∈[bmin,bmax],计算t=bΠ 3 计算q=k+t+τ 4 if q%2=0 then 5 q=Π−k+t+τ 6 if !T(q)then 7 k=2·k mod Π 8 Goto Step 2 9 返回q 算法8A中步骤1可以使用第2节中的3 个算法进行运算,步骤7可以通过移位和减实现,避免使用模乘,保证算法的高效性.应用中经常使用算法8A. 算法8中一些参数取特定值时还可以进一步简化,令参数u=1,t=0,a=65537,步骤1中k=65537,则算法可以简化为 其中α,v是满足要求的随机数,计算得到q后进行素数检测,如果不通过则重新选择α和v.根据文献[13]该方法是某主流密码设备厂商使用的RSALib 中的方法,文献[16]提出一种针对该算法的攻击——RoCA 攻击,使RSA 的密钥在较短时间内被恢复. 素数检测算法主要分为可证明素数检测和概率素数检测. 可证明素数检测是基于完整的数学推导,理论上可保证通过检测的肯定是素数,常用的可证明素数检测方法有n−1 分解法、Jacobi和测试法、基于椭圆曲线的素数检测法等,这些方法运算量都较大,耗时较长,在一般生成用于密码算法密钥参数时使用较少,本文不详述这类算法,可参考文献[10]和[13]. 概率素数检测算法在实际中使用更为广泛,这类算法相比于可证明素数检测算法计算量大大降低,但是其给出的结果有一定的可能性是错误的,即输入一个素数,这类算法给出的结果肯定是素数; 输入一个合数,算法检测后可能认为该数是素数. 常见概率素数检测类算法有Fermat 检测、Solovay-Strassen 检测和Miller-Rabin 检测三种算法. Fermat 检测是基于费马小定理,但是该类检测算法会将费马伪素数误认为是素数,而且需要进行模幂运算,运算量较大,实际中基本已经不再使用. Solovay-Strassen 检测的理论基础是欧拉准则,但是该检测算法会将欧拉伪素数误认为是素数,同时计算中需要计算“雅可比记号”(Jacobi Symbol),计算较为复杂.由于欧拉伪素数比费马伪素数少很多,因此该检测算法的正确率比Fermat 高.但是在Miller-Rabin 算法提出后该算法的使用少了很多. 算法9 Miller-Rabin(n,t)Input:待检测奇数n ≥3,检测迭代轮数t Output:n 是否是概率素数1 将n−1 写成n−1=2sr,其中r 是奇数2 for i=1 to t do 3 取随机整数a ∈[2,n−2]4 计算y=ar mod n 5 if y=1 且y=n−1 then 6 j=1 7 while j≤s−1 且y=n−1 do 8 y=y2 mod n 9 if y=1 then 10 返回“n 是合数”11 end 12 j ++13 end 14 if y=n−1 then 15 返回“n 是合数”16 end 17 end 18 end 19 返回“n 可能是素数” Miller-Rabin 的理论依据是定理6. 定理6取素数n,令n−1=2sr其中r是奇数.对任意整数a满足gcd(a,n)=1,均有ar≡1 modn或者a2/r≡−1 modn对某些j,0≤j≤s−1. Miller-Rabin 检测算法对于一些强伪素数[11]可能给出错误的判断.对于任一合数,经过Miller-Rabin(n,t)检测,认为是素数的概率不超过(1/4)t. Miller-Rabin 检测相对于Fermat 检测、Solovay-Strassen 检测效率要高很多,但是仍然需要进行模幂运算,因此实际使用中还有一些技巧提高素数检测的效率. (1)进行小素数试除 生成的候选值n可能含有小的素因子,因此在进行Miller-Rabin 检测前可以先进行小素数试除,分别计算Ri=nmodpi其中pi是选定的小素数,若存在Ri=0 则表明n是合数,通过小素数试除的候选值再进行Miller-Rabin 检测. (2)针对3.2节方法的进一步优化 若素数生成算法使用算法5,候选值依次加2,则在小素数试除过程中,计算Ri=nmodpi可以进一步提速.对于初始候选值n计算一次Ri=nmodpi将结果进行保存,则n=n+ 2时只需计算Ri=(Ri+2)modpi,可以将大数取模运算变成一次模加运算,有效提高效率. (3)Miller-Rabin 算法步骤4的优化 算法9中步骤4需要进行底数为a的模幂运算,模幂耗时较长; 但取a=2时,模幂运算可以简化,2r可以通过移位快速实现.使用Miller-Rabin 检测时需要取t个不同的a,因此在第一轮迭代中固定a=2可以有效提高整体检测效率. 本节对上述素数生成算法进行实验测试,对比分析了各算法的效率.测试使用Sage Math 编程,运行在Intel Xeon E5-1620@ 3.60 GHz 处理器的工作站.为了比较不同平台对算法性能的影响,将部分算法移植到智能卡进行了测试. 该小节对算法1–3的性能进行对比,算法生成一个输出的耗时与小素数个数k强相关,实验结果如图2所示. 图2 生成与小素数乘积互素数算法性能对比Figure 2 Performance comparison of generating a number co-prime with a product of small primes 图2可看出当k< 60时算法3有着明显性能优势,当k> 60时算法1的性能更好一些.但考虑到算法1要存储预计算值且一般取k<60,后续实验需要用到生成小素数乘积互素数时都选用算法3. 选择k=60 的情况在智能卡上进行实现,所需预计算在卡外进行.为了准确分析算法执行时长,采集功耗曲线进行分析(采集功耗曲线可以去除数据传输的时间,7816 接口数据传输较慢),算法1–3的功耗曲线如图3所示. 图3 智能卡上实现算法1–3的功耗曲线对比Figure 3 Comparison of power traces of Algorithm 1–3 on smart card 从图3中可以明显看出算法1调用模乘的次数,算法2–3调用模幂的次数.大量采集各算法执行时的功耗曲线,量取各次执行的时长,得到平均执行时长.算法1的平均时长7.5 ms,算法2的平均时长10.5 ms,算法3的平均执行时长6.7 ms,3 个算法相对执行时长与工作站的实验结果一致. 本小节对比第3节中介绍的素数生成主算法的性能,分别比较平均生成一个素数所需素数检测次数和平均时长. 由于算法6的性能与输入参数中选择素数的个数强相关,因此先分析素数个数对算法6性能的影响,如图4所示. 图4 算法6输入参数k 的不同取值算法性能对比(生成512 位)Figure 4 Performance comparison of parameter k’s value of Algorithm 6(generate 512 bits prime) 图4是生成512 bit 素数时,素数个数k取不同值对算法6性能(包括平均素数检测次数和平均耗时两方面)的影响,图中可以看出输入的素数个数越多,算法性能越好,因此在条件允许时使用尽量多的小素数.但是选择越多的素数,意味着需要越多的预存空间,因此实际使用时需要对时间和空间进行平衡和取舍.本文选择性能优先,在算法6性能尽量好的情况下,对比算法4–6、7A和8A五个算法的性能,结果如表2所示,表中数据是10 万次运算得到的平均值. 从表2可知算法4和算法5性能较差,平均时长和平均素数检测次数都没有优势; 算法7A和算法8A性能基本相当,文献[8]中提到原理上算法8A生成素数的分布均匀性比算法7A好,因此二者中优先考虑算法8A.表中算法6的素数检测次数比算法7A、8A多一些,但是平均执行时长更短,分析原因是算法6 的gcd()方法使用Sage Math 的系统函数,效率较高,而算法7A、8A中需要调用算法3,其中模幂使用二进制展开法实现,比Sage Math 的系统函数pow()1分析Python 中函数pow()的底层C 源码,指数长度不同时算法不同.性能低,此外算法8A中步骤7直接使用的系统模乘函数,未使用移位提速.因此在专用密码设备上使用相同的底层算子实现算法时,算法8A和算法6时间基本相当,甚至会更快一些,对于生成较短的素数时算法8A的平均素数检测次数更少. 表2 素数生成主要算法性能对比Table 2 Performance comparison of main step of prime generation 此外需要注意,表中的平均执行时长与处理器结构有关,甚至算法间的相对时长也有差异.使用Intel Core i5 8250 4 核8 线程处理器执行同样的程序,生成1024 比特的素数时,算法8A的执行时长为5.61 ms而算法7A的平均执行时长为5.80 ms.因此,平均素数检测次数更值得关注. 素数在密码学领域有着大量的应用,常见的非对称密码算法RSA 中使用了大素数.RSA 算法基本原理如下. 选择两个大素数p和q,计算n=pq,随机选取加密密钥e,使p与(p−1)(q−1)互素,然后计算解密密钥d=e−1mod((p−1)(q−1)).e和n作为公钥,d是私钥,p,q不再需要,通过安全方式将其丢弃.加密消息m时计算c=memodn,解密时计算m=cdmodn.可以通过CRT 方式提高运算速度.为了获得最大程度的安全性,一般取p和q长度相等,同时还要保证p和q不是很接近. 应用中,通常使用相同的公钥e(常取3 或65 537),因此生成算法参数p和q时就要保证(p−1)(q−1)与e互素.本节选择对算法3和算法8进行改进,使之生成的素数p能够满足gcd(e,p−1)=1. (1)e是一个素数.只需在p的素性检测后判断pmode是否等于1,若等于1 则重新生成素数. (2)e的所有素因子ei均满足ei|Π. 取整数α使之满足gcd(α,Π)=1 且αei−1≡1 modei对所有ei均成立.记e+=gcd(e,Π).令算法3步骤1的初值c≡αmode+,可以取c=α+re,r为随机数.再令算法8步骤4中a=α2,因为e+|Π,所以可保证算法8生成p的序列始终满足p≡α2j+1mode+,其中j为整数.因此对所有的ei均有p≡1 modei成立,故可保证gcd(e,p−1)=1. (3)e不是素数且存在素因子ei∤Π.由(2)可知当ei|Π时,通过对算法3和算法8的部分参数进行特定取值可以保证p≡1 modei,故只需对ei∤Π验证p≡1 modei是否成立.可以使用定理2进行判断,记只需判断(p−1)λ(e−)≡1 mode−是否成立,若不成立则重新生成素数. 综上所述,只要算法3步骤1取c=α+re,算法8步骤4中a=α2,再加一步额外的判断即可使用算法3和算法8直接生成满足要求的RSA 的参数p和q. 不同应用中对素数有不同的要求,可以根据相应的要求对算法进行适当的改造,使算法能够直接生成满足要求的素数.文献[6]和[8]给出了生成安全素数、应用于ANSI X9.31、生成强素数等多种不同场景下算法的改造. 本文对近年来提出的一些快速素数生成算法进行归纳、总结和对比.将素数生成过程分为初值生成、增量变换和素性检测3 个过程,分别介绍了每部分的算法,给出了各算法必要的理论基础,分析了算法的演进过程,并给出一些算法实现中的技巧,提到了部分算法的安全性. 本文通过实验验证了各算法的性能,给出了各算法性能的对比数据,由实验结果可知改进的增量素数生成算法(算法6),改进的M-J 素数生成算法的特例(算法8A)分别结合改进的模搜索法(算法3)这两种方案整体性能较好.本文还给出了素数生成算法在RSA 算法中的应用. 本文仅给出了各算法的基本形式和性能分析,实际用于密码设备时还需要考虑算法实现[17]的安全性,考虑是否有侧信道信息的泄漏[18],考虑结果分布是否均匀等,用于RSA 算法时还需要保证使用的素数是强素数[19].
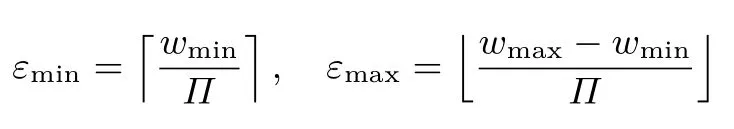


3.5 改进的M-J 素数生成算法


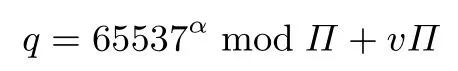
4 素数检测算法
4.1 概率素数检测算法

4.2 素数检测效率的提高
5 实验结果
5.1 生成与小素数乘积互素数算法性能对比


5.2 素数生成主算法性能对比

6 应用
7 结论

