整数剩余类环上本原序列在Garner分解下最高权位的保熵性*
孙翔宇,陈华瑾,朱宣勇
信息工程大学 数学工程与先进计算国家重点实验室,郑州450001
1 引言
序列密码,也称流密码,是现代密码学的重要分支之一,广泛应用于军事、外交、政府以及商业的通信安全领域,比如WEP 中的RC4[1]、3GPP 中的SNOW 3G[2]和ZUC[3]等都是序列密码算法.
传统的序列密码通常采用两步走的设计思路,即线性驱动+ 非线性改造.线性驱动可以为整个密码系统提供具有理想统计特性的初始乱源,通常采用二元域上的极大周期线性反馈移位寄存器序列; 非线性改造部分用来掩盖驱动序列的线性性质,通常的改造方式有非线性组合、非线性过滤和钟控[4].尽管改造方式多样,但随着密码分析技术的不断发展,线性序列源的特点被密码分析者不断挖掘并利用.传统的序列密码设计暴露出越来越多的安全隐患,很难抵抗相关攻击[5]和代数攻击[6],这使得序列密码从线性序列源向非线性序列源转变,比如eSTREAM 项目的全部三个面向硬件的胜选算法Trivium、Grain v1和MICKEY v2 均采用非线性驱动序列.
环上导出序列就是一类重要的非线性序列,其非线性来自对整数剩余类环上线性递归序列的压缩,3GPP 中的ZUC 所使用的序列源就是一类环上导出序列.整数剩余类环上线性递归序列的研究起源于二十世纪二三十年代,当时M.Ward 等学者[7,8]从纯数学的角度出发研究了多项式的周期、序列的周期、序列的特征多项式和极小多项式等一些基本性质.到八十年代,在密码学背景下,整数剩余类环上线性递归序列由于其线性本质,很难直接应用于密码学,压缩的思想开始萌芽.第一类压缩导出序列是权位压缩导出序列,它由我国学者黄民强和戴宗铎[9]以及俄罗斯学者Kuzmin和Nechaev[10]分别独立提出.这类序列主要设计思想是利用p-adic 分解和权位压缩将环Z/(pe)上的序列的信息无损地压缩到Z/(p)上,从而得到Z/(p)上具有复杂非线性结构的序列.随后,大量文章研究了这类序列的线性复杂度、元素分布、自相关等伪随机性质[11–14],研究结果表明,这类序列是一类具有优良密码性质的非线性序列.在此过程中,信息无损压缩也得以从数学上完整地刻画.
整数剩余类环上线性递归序列的信息无损压缩,也被称为环上导出序列的保熵[9,15],在数学上表现为原序列与压缩后的导出序列之间的一一映射关系.保熵性从理论上可以保证压缩导出序列含有原序列的所有信息.特别的,由保熵性直接可以得到压缩导出序列的周期和原序列相等.而对权位压缩导出序列的其它伪随机性研究表明,压缩后序列的游程分布、自相关、互相关等性质都很理想.这使得对环上导出序列的研究几乎等同于对保熵性的研究,即研究具有保熵性的压缩函数.2000年左右,结合环上导出序列和FCSR 序列,另一类压缩导出序列——模压缩导出序列被提出.这类序列的主要思想是采用模压缩来破坏原序列的线性结构,从而产生丰富非线性性.文献[16]证明了环Z/(pe)上本原序列模M 的保熵性,其中M含有一个异于p的素因子,文献[17]中首次研究合数环Z/(pq)上模压缩导出序列的保熵性,文献[18]对上述结果进行改进,证明了几乎所有Z/(pq)上次数n≥2 的本原多项式生成的本原序列都是模M保熵的,其中M>2 且有一素因子与pq互素.进一步,文献[19–22]研究了环Z/(N)上本原序列的元素的分布特性,进而给出了模M的保熵性,其中N是两个或两个以上不同奇素数乘积,M含有一个素因子与N互素或者M=0 mod 4.胡志等在文献[23]中同样给出了无平方因子环上模保熵性类似的结论.紧接着程源在文献[24]中给出了环Z/(peq)上的模压缩保熵序列.这些结果对ZUC 序列源的设计提供理论依据.
保熵性是环上导出序列的重要理论支撑,也是环上导出序列的核心研究内容,不同的保熵压缩函数为环上导出序列的进一步密码应用提供了丰富素材.本文提出一类新的保熵压缩函数,即整数剩余类环上本原序列Garner分解下的最高权位的保熵性.具体的,本文针对一般的整数剩余类环Z/(N),将Garner 分解[25]与中国剩余定理相结合,提出了环上序列在Garner分解下的分位序列的高低权位概念,并证明了部分情况下分解的最高权位序列是保熵的.这意味着,将Z/(N)上的本原序列压缩到符合条件的环上时,其中可以得到保留Z/(N)上本原序列全部信息的一条非线性序列.特别地,当我们选取适当的N(例如N=M·216且M是奇数)时,可以得到拥有理想的周期特性,复杂的非线性结构以及易于软硬件实现的非线性序列.
本文第2 节给出预备知识,第3 节证明主要结论,最后第4 给出小结.
2 预备知识
2.1 中国剩余定理和Garner 分解
中国剩余定理又称孙子定理,它来源于线性同余方程组求解问题.
中国剩余定理:设N=P1P2···Pr,其中P1,P2,··· ,Pr是两两互素的正整数,那么对于整数a∈Z/(N)有如下分解

这里aPi≡a(modPi),N=PiQi(1≤i≤r),以及Q−1i是满足

的一个整数(即是Qi模Pi的逆).
例1N=40=5×8,那么a≡16aP1+25aP2(mod40),取a=36时,那么aP1=1,aP2=4.
Garner 分解:设N=P1P2···Pr,其中P1,P2,··· ,Pr是两两互素正整数,那么对于整数a∈Z/(N)有如下分解
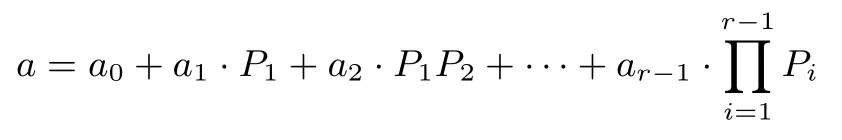
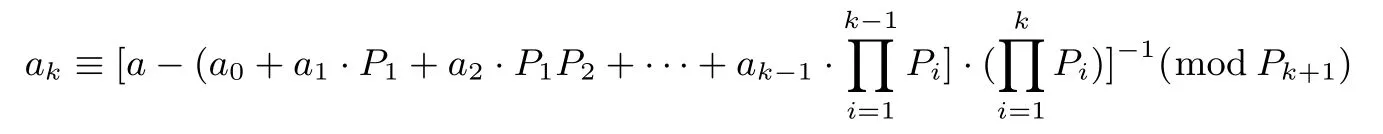
例2N=40=5×8,那么a≡a0+a1·5(mod40),取a=36时,那么a0=1,a1=7.
中国剩余定理本质上是环Z/(N)到Z/(P1)×Z/(P2)×···×Z/(Pr)的一一映射,即Z/(N)上的数a和唯一的一组(aP1,aP2,··· ,aPr)一一对应,其中aPi∈Z/(Pi),1≤i≤r.而Garner 分解可视为环Z/(N)到Z/(P1)×Z/(P2)×···×Z/(Pr)的一一映射,即Z/(N)上的数a和唯一的一组(a0,a1,··· ,ar−1)一一对应,其中ak∈Z/(Pk+1),0≤k≤r−1.如上两例:N=40=5×8,取a=36时,在中国剩余定理分解下对应于数组(1,4),在Garner分解下对应于数组(1,7).
2.2 环上序列基本概念
定义1[13](序列-序列的特征多项式)设整数N> 1,f(x)=xn−cn−1xn−1−···−c0是整数剩余类环Z/(N)上的n次首一多项式.若Z/(N)上序列满足递归关系式

其中i≥0.则称上由f(x)生成的n阶序列,称f(x)是的特征多项式.称次数最小的特征多项式为的极小多项式.
通常我们将环Z/(N)上由f(x)生成的n阶线性递归序列之集记为G(f(x),N).在定义1中,若f(0)是环Z/(N)中的可逆元,即gcd(f(0),N)=1,则存在正整数T,使得f(x)整除xT−1.最小的这样的正整数T称为f(x)的周期,并记为per(f(x),N).当N=pe时,per(f(x),N)≤pe−1(pn−1)[9].当时

定义2[9](环Z/(pe)上本原序列)设pe是素数方幂,上的n次首一多项式.若则称上的n次本原多项式.进一步,若序列且则称是Z/(pe)上由f(x)生成的n阶本原序列.
当f(x)是Z/(pe)上的n次本原多项式时,对任意的i∈{1,··· ,e−1},f(x)modpi也是Z/(pi)上的n次本原多项式,即per(f(x),pi)=pi−1(pn−1).特别地,f(x)(modp)是Z/(p)上的n次本原多项式.
定义3[18](环Z/(N)上本原序列)设是N的标准分解,f(x)是Z/(N)上的n次首一多项式.若对每个上的n次本原多项式,则称f(x)是Z/(N)上的n次本原多项式.进一步,是Z/(N)上由f(x)生成的n阶线性递归序列,若对每个1≤i≤r,上的n阶本原序列,则称是Z/(N)上(由f(x)生成)的n阶本原序列.
由定义3可知,环Z/(N)上n次本原多项式的周期和n阶本原序列的周期相等,记为TN,则

通常我们将环Z/(N)上由f(x)生成的所有本原序列之集记为
保熵旨在刻画将环Z/(N)上的一条本原序列无损地压缩到环Z/(M)上的一条压缩导出序列,使得压缩前后序列的信息量不变.用数学语言描述,设N≥3 的整数,整数上的n阶本原序列,是Z/(M)上的一条压缩导出序列,f(x)是Z/(N)上的本原多项式,选取压缩映射φ使得压缩映射

命题1[16](环Z/(pe)上本原序列的模保熵性)设p是素数,M是正整数,它含有一个异于p的素因子.设e是正整数,f(x)是Z/(pe)上本原多项式,则当且仅当
2.3 Garner分解下的最高权位序列
设N=P1P2···Pr,其中P1,P2,··· ,Pr是两两互素的正整数,则对Z/(N)上的本原序列由中国剩余定理可知:
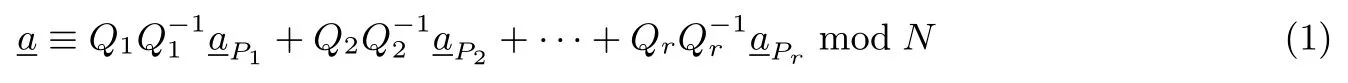
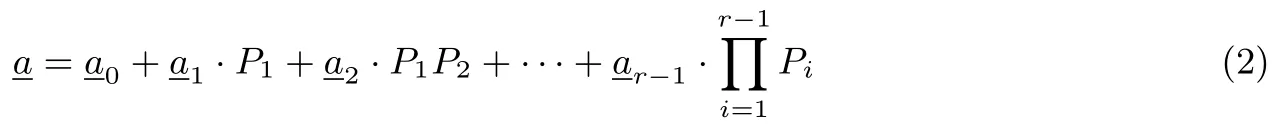

在数的分解意义下,中国剩余定理分解和Garner 分解具有等价性,即给定Z/(N)上的数a,既和数组(aP1,aP2,··· ,aPr)一一对应,也和数组(a0,a1,··· ,ar−1)一一对应,如例1和例2,其中aPi∈Z/(Pi),aj∈Z/(Pj+1),1≤i≤r,0≤j≤r−1.但序列的中国剩余定理分解和Garner 分解却有很大的区别:中国剩余定理分解下的分位序列地位等价,没有高低权位之分——或者说序列共同决定了序列而实验显示Garner 分解的分位序列中决定其他分位序列,进而决定序列换句话说,整数剩余类环上序列在Garner分解下存在最高权位序列.
下面将对部分情形中整数剩余类环上序列在Garner分解下有最高权位序列的保熵性进行证明.
3 Garner分解下最高权位序列的保熵性
设N=P1P2···Pr,其中P1,P2,··· ,Pr是两两互素的正整数.首先给出序列在中国剩余定理分解和Garner分解下的命题.
命题2设是Z/(N)上的本原序列,其中国剩余定理分解和Garner 分解分别为(1)式和(2)式,则是Z/(P1)上的本原序列.
证明:对两个分解式分别进行模P1运算可以得到由定义3知是Z/(P1)上的本原序列,故命题得证.
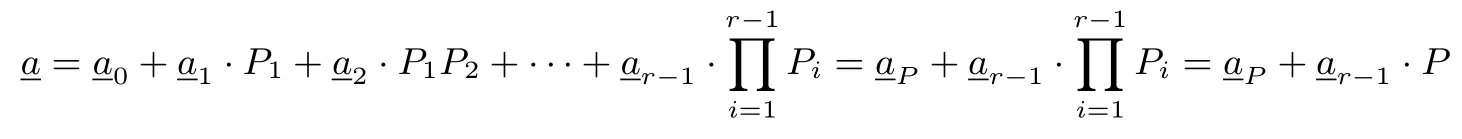
在给出主要结论之前,首先给出下面引理.
引理1设正整数N=PQ,其中gcd(P,Q)=1,f(x)为Z/(N)上的n次本原多项式,序列a∈的Garner 分解为令h(x)≡xTP−1(modf(x),Q)且a≡其中且P·P−1≡1 modQ,则

证明:因为f(x)为Z/(N)上的n次本原多项式,所以xTP−1≡0(modf(x),P).这意味着

又因为h(x)≡xTP−1(modf(x),Q),所以

联立(3)式和(4)式,由中国剩余定理得:
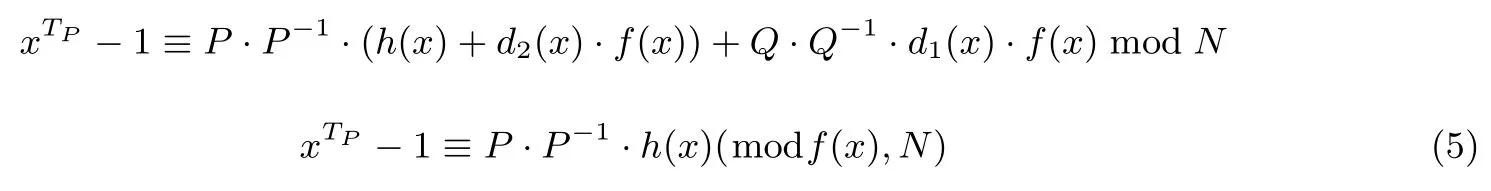
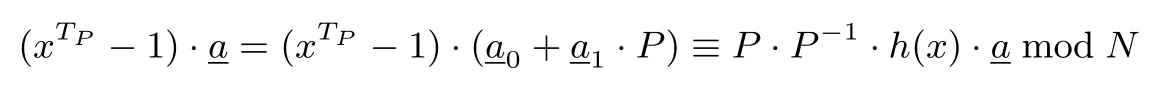
于是

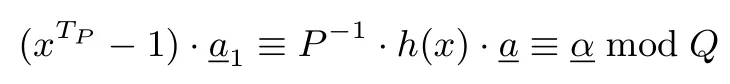
引理得证.
定理1(环Z/(N)上序列的最高权位保熵性)设正整数N=PQ,其中gcd(P,Q)=1,序列是Z/(N)上两条本原序列,其Garner 分解分别为若P 证明:由可得所以由可得,必要性得证.下面来证充分性.即证当时 也即 对(8)式取模Q可得 注意到定理1中需要条件P 定理2(环Z/(peq)上序列的最高权位保熵性)设正整数N=peQ,其中p是素数且与Q互素,序列是Z/(N)上两条本原序列,其Garner 分解分别为若则当且仅当 证明:必要性显然.下面来证充分性.仍然对序列分别进行中国剩余定理分解和Garner 分解,并将两分解式相减,考虑到由(9)式可知 等式(12)右端实质上是对环Z/(pe)上序列的模Q压缩.在这种情形下,可以利用命题1 来完成证明.具体地, 考虑到密码应用,通常希望压缩后的序列是适应计算机字长的.定理1和定理2给出的压缩序列是环Z/(Q)上的,所以下文取Q=2r.此外,为了易于实现,原始环上线性递归序列所在的环Z/(N)的模数N也应慎重选择,由于N为含素数方幂的合数,所以具有形式N=2m−1,其中m=8,16,32,64,···是最理想的参数选择,其次选择N=2m−2i±2j,其中m=8,16,32,64,··· 这些参数方便原始序列在计算机平台实现,而且实现代价较低[26]. 若采用定理1的保熵压缩方式,需要条件P 例3当N=(216−1)·216,对于任意奇数次本原多项式,条件T216∤T216−1均成立; 若本原多项式的次数是小于500 的偶数,通过实验容易验证条件T216∤T216−1也成立. 若采用定理2 的保熵压缩方式,即P=pe,Q=2r.设本原序列的次数为n,那么条件TQ∤Tpe等价于2r−1(2n−1)∤pe−1(pn−1),其中p是奇素数.下面给出例4和例5. 例4当N=(228−216+1)·24,对多项式次数n<500时的实验表明,只要n不取1,2,3,4,6,8,12,14,16,均满足T24∤T228−216+1. 例5当N=(224−24−1)·28,对多项式次数n<500时的实验表明,只需n不取8,24,均满足T28∤T224−24−1. 上述例子中的多项式次数还可以进一步增大,考虑到密码应用,本文只对500 次以内的本原多项式进行了验证.通过例3 可以从环Z/((216−1)·216)上的一条本原序列压缩导出环Z/(216)上的一条非线性序列,压缩比大约为2:1(即将32 比特的数压缩到16 比特).若想进一步提高压缩导出序列的非线性程度,可以选择例4 中的参数,这样就可以得到环Z/(24)上的一条非线性序列,压缩比达到8:1(即将32 比特的数压缩到4 比特).通过本文的结论可以得到更多拥有理想的周期特性,复杂的非线性结构以及易于软硬件实现的非线性序列. 在给定四元数组(n,p,e,r)时,条件2r−1(2n−1)∤pe−1(pn−1)是非常容易判断的.最后,本文给出上述条件成立的一个简洁的充分条件. 命题3设四元数组(n,p,e,r)如上描述,若r≥3,p≡3 mod 4,n为奇数,必有2r−1(2n−1)∤pe−1(pn−1). 证明:(反证)若2r−1(2n−1)|pe−1(pn−1),因为gcd(2,p)=1,所以必有2r−1|pn−1,注意到p≡3 mod 4,那么p2≡1 mod 4.因为n为奇数,所以pn≡p≡3(mod 4),故pn−1=2+4k=2(2k+1),其中k≥0.又因为r≥3,所以2r−1≥4,故2r−1∤2(2k+1),即2r−1∤pn−1.命题得证. 注1例3 中当参数n为奇数时恒成立的证明同命题3证明类似. 本文首次讨论了整数剩余类环上序列在Garner分解下最高权位序列的保熵性.与已有的Z/(pe)上的权位压缩保熵及Z/(N)上的模压缩保熵方式不同,这是一种新的压缩保熵映射.注意到以往的环上序列的结果主要在素数方幂和无平方因子环上讨论,含平方因子环也仅对环Z/(peq)进行了研究.本文结论给出了范围更广的合数环上的压缩导出序列,并给出了部分情形下的整数剩余类环上序列在Garner分解下最高权位序列的保熵性证明.此外,通过选取合适的参数,可以得到拥有理想的周期特性,复杂的非线性结构以及易于软硬件实现的非线性序列.这为环上导出序列的进一步应用提供更多理论支撑.同时,实验显示,整数剩余类环上序列在Garner分解下最高权位序列的保熵性普遍成立,但本文只给出部分情形的证明.寻找新的方法对这类保熵性进行进一步证明是我们下一步的研究目标.

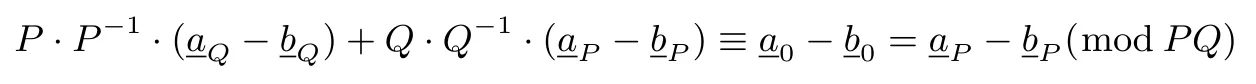
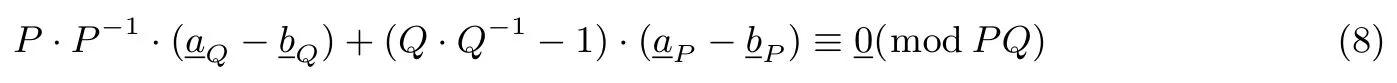


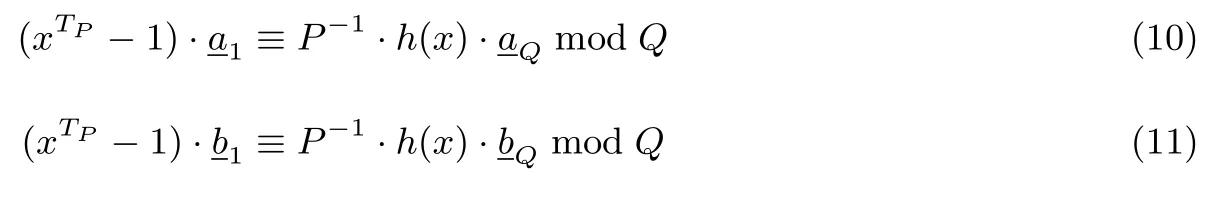


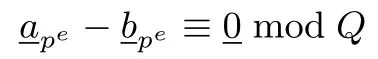
4 小结

