隐私保护的点与任意多边形位置关系判定*
张明武,冷文韬,沈 华
1.湖北工业大学 计算机学院,武汉430068
2.桂林电子科技大学 计算机与信息安全学院,桂林541004
3.智能地学信息处理湖北省重点实验室,武汉430074
1 引言
随着移动互联网和大数据相关技术的不断发展,人类社会的信息量越来越多,隐私问题日益突出.例如,为了让企业领导者了解员工是否到达指定的工作区域,员工需要报告自己的具体坐标位置,同时员工也被告知工作区域的具体信息.员工的具体坐标位置属于员工的个人隐私信息,工作区域的具体信息属于企业的隐私信息,因此,上述应用场景中存在隐私泄漏问题.如何在不泄漏员工隐私信息和企业隐私信息的条件下企业领导者可以了解掌握员工到达指定工作区域的情况,是一个亟待解决的问题.在另外一个应用场景中,某个调查机构需要调查统计指定区域的车流量情况,为了保证调查的有效性该调查机构必须保密被调查区域的信息同时利用车辆的位置信息得到统计结果.车辆的位置信息属于车辆使用者的隐私信息,因此,该应用场景中也存在隐私泄漏问题.如何在不泄漏车辆位置信息和被调查区域信息的条件下调查机构获得该区域的车流量情况,也是一个值得研究的问题.上述这些问题可以被抽象为具有具有隐私保护的点与多边形关系判定问题,该问题主要涉及到具有隐私保护的多方几何计算.具有隐私保护的多方几何计算属于安全多方计算(secure multi-party computation,SMC)[1–3]研究领域.SMC 实现了在分布式环境下,多个互不信任的参与者在不泄漏自己输入的前提下协作完成指定的计算.SMC 的具体应用领域主要有:数据挖掘[4]、计算几何[5]、比特币交易[6]等.
点与多边形的位置关系判定[7](point-in-polygon problem,PIPP)是计算几何中的常见问题.解决该问题的方法有射线法[8]和面积法以及夹角法[9]等.其中射线法是指,通过判定点引出一条射线,计算该射线与多边形的交点数,若交点的数为奇数,则坐标点在多边形内部,否则坐标点在多边形外[8].在具有隐私保护的点与多边形关系判定问题中,参与双方中的一方拥有一个点另一方拥有一个构成多边形的顶点集合,在不泄漏各自输入信息的前提下,双方协作完成点与多边形的位置关系判定,并且双方也无法从判定结果中推测出对方的输入.文献[2]基于Monte Carlo 方法和Cantor 编码设计了点包含与图形包含问题的近似解决方案,该方案将问题转化为集合包含问题,利用了可交换加密,是一种近似求解问题的方法,其精度与复杂度成正比,存在一定误差.点包含问题是指,判断判定点是否位于指定区域内.点包含问题是点与多边形位置关系中的一种.文献[5]基于安全两方点积协议和向量控制协议,首次解决了安全两方点包含问题,该方案调用了数次百万富翁协议,导致协议的复杂度较高.文献[10]将点包含问题转化为三角形面积问题,并基于内积协议给出解决三角形面积问题的方案.该方案受制于问题转化方法的局限性并不适用于凹多边形的情况.文献[11]提出了一种茫然安全点线位置关系判断协议,并利用该协议解决了点包含问题,该方法基于茫然传输和百万富翁协议,其效率不高,并且无法适用于复杂的任意多边形.文献[12]基于内积协议设计了一种具有隐私保护的点与直线距离的计算协议,解决了隐私保护的直线与圆圈的相交问题.文献[13]提出了安全的两方向量叉积协议以及安全的点与线叉积协议,协议必须调用百万富翁协议,其复杂度与多边形的边数有关,且仅支持普通凸多边形.文献[14]在云外包环境下将点与面的位置关系等转化为夹角问题,并设计了基于云外包条件的内积协议,但该协议无法适用于任意多边形情况.文献[15]使用角度旋转法解决了点与多边形的关系判定问题,该方案虽然解决了点与任意多边形的关系判定,然而其计算复杂度较高.由于实际应用中人们往往面临的是点与凹凸多边形结合的复杂图形的位置关系判定,因此,研究和设计点与任意多边形的位置关系判定协议具有很重要的应用价值.但目前缺少高效安全地求解点与任意多边形关系判定问题的方案.
针对上述问题,本文首先基于文献[12]提出的编码方式设计了一种精简高效的叉积协议,该协议实现了具有隐私保护的点与直线相对位置的判定,然后在该叉积协议的基础之上本文结合射线法提出了一种具有隐私保护的点与任意多边形关系判定方案.
本文的主要贡献有:(1)提出了一种具有隐私保护的点与任意多边形关系判定的方案,该方案同时适用于凸多边形与凹多边形的情况.(2)设计了一种高效的叉积协议,该协议基于明文空间数域划分的思想实现了支持负数的叉积运算,提升了判定方案的效率.(3)提出了一种高效的转化方法,将点与任意多边形位置关系的判定问题转化为任意一条过点的射线与多边形相交的点数奇偶性的判定问题.
2 设计目标及安全性定义
2.1 安全性定义
本文的安全目标是,参与计算的两方均无法获得对方的输入信息.本文在半诚实参与者安全模型下达到该安全目标.半诚实参与者是指能够严格遵守协议的执行指令,在协议的执行过程中记录所有得到的中间结果并企图根据自己获得的信息推测出额外信息的参与者.基于该安全模型,如果参与者可以利用自己的输入和协议的输出单独模拟整个协议的执行过程并且在此过程中得不到任何额外的信息,那么该协议就能保证参与者输入的安全性.上述安全性的形式化定义如下:
假设两个参与者要计算函数f:{0,1}∗×{0,1}∗→{0,1}∗×{0,1}∗,其中f1(x,y)和f2(x,y)分别代表f的第一个元素和第二个元素;π表示计算f的协议;S1和S2是两个多项式时间算法,它们作为模拟器模拟协议的执行过程.Si(x,f(x,y))表示模拟器以第i个参与者的输入和协议的输出作为参数模拟协议的执行过程,表示第i个参与者的视图表示第i个参与者执行协议得到的结果,其中i=1,2.对于确定性功能函数f,我们称协议π在半诚实模型下秘密的计算f当且仅当S1和S2是使得

其中|x|=|y|.
2.2 设计目标
基于上述安全模型,本文设计目标是提出一种具有隐私保护的、高效的点与任意多边形关系判定方案.具体来说,提出的方案需要达到下述设计目标:
(1)安全性.通过执行方案,双方在不知道对方输入信息的情况下协作完成点与多边形的位置关系判定,并且双方也无法从判定结果中推测出对方的输入,即方案必须满足2.1节提出的安全性要求.
(2)正确性.对在凸多边形内或外的任何点,方案都能得到正确的判定结果; 对在凹多边形内或外的任何点,方案都能得到正确的判定结果.即,针对任意多边形,方案都能够正确判定点和多边形的位置关系.
(3)高效性.为更具实用性,方案应有效减少参与双方之间的通信开销和每个参与方的计算开销.
3 预备知识
3.1 叉积
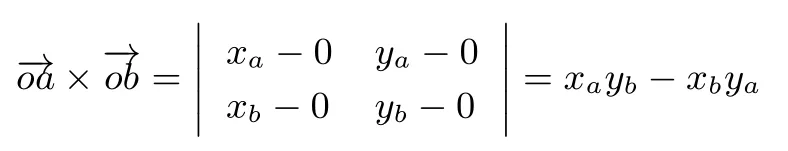

图1 叉积定义Figure 1 Definition of cross product
3.2 同态加密
同态加密是一种允许对密文进行计算的一类加密算法.在将明文加密后,对密文进行有限的加法或乘法运算后仍可以解密,解密后的结果与对明文的操作是一致的,从而达到对密文数据计算的目的.Paillier公钥密码系统[17]是一种常见的同态加密算法,其主要包括三个算法:密钥产生算法(Gen)、加密算法(Enc)和解密算法(Dec).该加密算法的同态性主要体现在以下方面:

其中m1和m2是消息空间中的两个消息,r1和r2是两个随机数.
3.3 点与直线位置关系
文献[16]已证明点与直线的位置关系等价于求点与直线的叉积,可以通过求点与直线的叉积来判断点与直线的位置关系.点p0=(x0,y0)与直线的关系(其中p1=(x1,y1),p2=(x2,y2))定义如下.
定义1(点与直线的关系)计算点p0与直线的叉积


将点与直线的位置关系表示为:

3.4 点与任意多边形的位置关系
文献[18]给出并证明了关于点与任意多边形位置关系的如下定理.
定理1点与任意多边形的位置关系等价于过判定点的任意射线与任意多边形相交的点数,若相交点数为奇数则判定点在多边形内,否则在多边形外.
4 隐私保护的点与多边形关系判定
4.1 问题描述和转化
4.1.1 问题描述
设Alice 拥有一个点p0=(x0,y0),Bob 拥有一个由n个顶点{p1=(x1,y1),p2=(x2,y2),··· ,pn=(xn,yn)} 构成的任意多边形P,在不泄漏双方各自信息的情况下,Alice和Bob 协作判断Alice 拥有的点p0是否在Bob 的任意多边形P内.
4.1.2 问题转化
本文基于模拟射线法的思路将点与任意多边形位置关系的判定问题转化为任意一条过点的射线与多边形相交点数的奇偶性判定问题.为了便于描述,本文提出了同侧点的概念,其定义如下.
定义2(同侧点)经过点的直线等价于两条以该点为顶点并且方向相反的射线,其中同一条射线上的点称作该点的同侧点.
基于同侧点的概念,本文给出了实现问题转化的定理.
定理2过判定点作直线,直线与多边形的交点中同侧点的数量等价于过判定点射线与多边形的交点数,若交点数为奇数则判定点在多边形内,否则判定点在多边形外.
证明:已知一条直线可被判定点划分为两条方向相反的射线,若直线与多边形相交,显然这些交点分别存在于两条方向相反的射线上,因此可统计得到判定点的同侧点数,由定理1结论可知定理2成立.
定理3若多边形的顶点全部位于直线的同一侧,则直线与多边形不相交.
证明:假设直线与多边形相交,那么必定存在一个顶点在直线上或在直线的另一侧,命题得证.
定理4过判定点做任意一条直线,若直线与多边形不相交,则判定点必定在多边形外.
证明:假设判定点在多边形内,过判定点任意做一条直线,由于直线的性质其必定会与多边形相交,因此假设不成立,命题得证.
基于定理2–4,点与任意多边形位置关系的判定被转化为任意一条过点的射线与多边形相交点数的奇偶性判定.例如,图2和图3中的点p0和任意多边形的相对位置可以通过统计点p0的同侧点数并根据同侧点的奇偶性得到.

图2 点p0在多边形外Figure 2 Example of a point outside a polygon
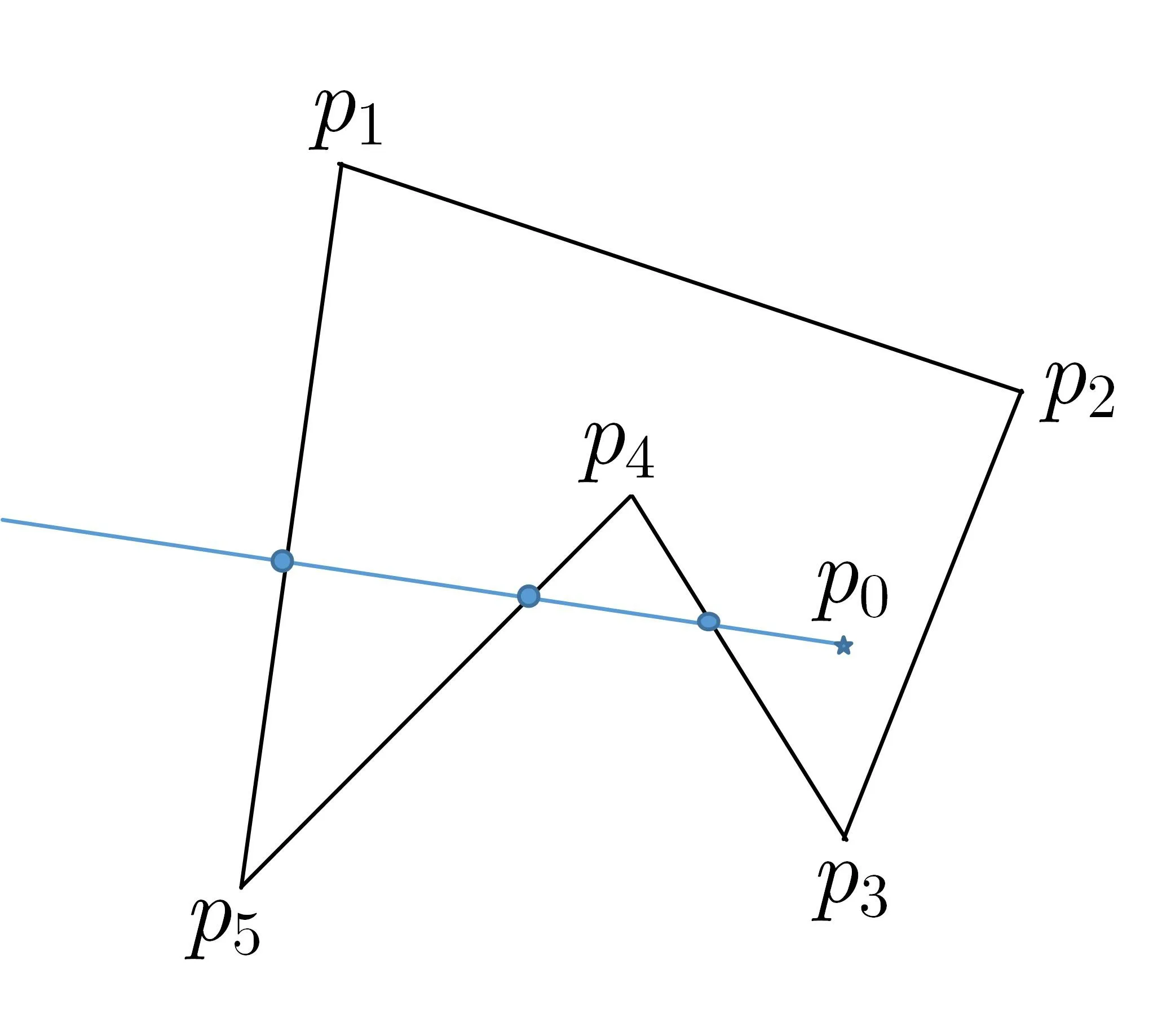
图3 点p0在多边形内Figure 3 Example of a point inside a polygon
为了方便表达,定义如下谓词:

根据定义1可知叉积协议是一种用来解决点与直线位置关系判定的工具,文献[16]中提出的具有隐私保护的叉积协议虽然能保密的判定点与直线的位置关系,但是其需要调用复杂度较高的密码学原语.本文设计了一个轻量级的叉积协议用于判定点与直线的位置关系.针对任意一条过点的射线与多边形相交点数的奇偶性判定问题,基于该轻量级叉积协议,本文给出的判定方案包括3 个步骤.
步骤1:首先任取一点p′与判定点p0组成一条直线
步骤2:根据叉积协议,计算得到多边形P的顶点与直线的相对位置关系,从而找出多边形与直线相交的所有边;
步骤3:根据叉积协议,计算得到判定点p0与相交边的相对位置关系,从而获得以判定点为顶点的同侧点数,若同侧点数为奇数则判定点p0在多边形P的内部,若为偶数则判定点p0在多边形P的外部.
4.2 具体方案
本文提出的具有隐私保护的点与任意多边形位置关系的判定方案包括两个协议:具有隐私保护的点与直线位置关系判定协议和具有隐私保护的点与任意多边形位置关系的判定协议.首先由Alice和Bob分别根据安全参数生成各自的Paillier 加密算法的公私钥对(PKA,SKA)和PKB,SKB,然后Alice和Bob 执行具有隐私保护的点与任意多边形位置关系的判定协议,使得Alice和Bob 在保证自己的输入信息不被泄漏的情况下均知道点p0是否在多边形P中.在执行点与任意多边形位置关系的判定协议的过程中,具有隐私保护的点与直线位置关系判定协议将被调用以协助完成点与任意多边形位置关系的判定.本文使用文献[12]中支持符号位的编码方式,对于明文空间{0,1,··· ,T},设L=⌊logT⌋+1,将明文空间中的元素表示成长度为L的二进制数,将其中的第L位视为符号位.根据符号位的值,本文将明文空间分成正负两个部分.L为1 的元素构成明文空间的负数空间,L为0 的元素构成明文空间的正数空间.点的坐标范围为[−T/2,T/2].当点坐标落在范围[0,T/2]内时,将该坐标映射到明文空间的正数空间,此时只需直接映射即可; 当点坐标落在范围[−T/2,0)内时,将该坐标映射到明文空间的负数空间,此时通过将坐标值加上T进行映射.协议的具体内容描述如下.
协议1隐私保护的点与直线位置关系判定
步骤1.点的拥有者基于自己公钥利用加密算法Enc 对点进行加密,得密文集合

步骤2.点的拥有者将发送给直线的拥有者,直线的拥有者选取随机数r并做如下计算:

并将计算结果(M,W,K)发送给点的拥有者.
步骤3.点的拥有者接收到(M,W,K)后做如下计算.

步骤4.点的拥有者将结果告诉直线的拥有者.
协议2隐私保护的点与任意多边形位置关系判定
输入:Alice 拥有点p0(x0,y0),Bob 拥有多边形P={pj(xj,yj),j∈(1,··· ,n)}.
输出:Alice和Bob 均得到点p0(x0,y0)与多边形P的位置关系.
步骤1.Alice 随机选取点p′(x′,y′),构造直线
步骤 2.以直线和多边形的顶点pj(xj,yj)作为输入,使用Bob 的公钥执行协议1,即其中j=1,2,··· ,n,协议被执行了n次,将n次执行得到的结果记为
步骤3.Bob 在R中筛选出满足下述Cross 条件的元素组其中1≤j 将所有满足 Cross 条件的元素组对应点构成的直线构成的集合记为ICross),即ICross=其中1≤j 步骤 4.以点p0和线段∈ICross作为输入,使用 Alice 的公钥执行协议1,即协议被执行了|ICross| 次,将|ICross| 次执行得到的结果记为R′=若∃0 ∈R′,则点p0在多边形P内,即f(p0,P)=1; 若R′中–1或1 的个数为奇数,则p0点在多边形P内,即f(p0,P)=1; 若R′中–1 或1 的个数为偶数,则p0点在多边形P外,即f(p0,P)=0. 步骤5.Alice 将结果f(p0,P)发送给Bob. 5.1.1 协议1正确性分析 协议1的目标是安全计算如下公式: 由加密同态性可得: 显然,当把负值映射到明文空间的负值空间后,对其进行同态运算会导致明文数值上的偏移.协议1将公式(13)中的减法运算均安排在解密之后进行,保证加密过程中的明文为正数. 因此,协议1能够得到正确的计算结果. 5.1.2 协议2正确性分析 将点p0与随机选取的点p′确定的直线与多边形P的顶点作为输入,执行协议1得到多边形P的各个顶点与直线的位置关系,即集合R.基于5.1.1的证明可以保证集合R的正确性.若R中的元素全部为1 或–1,则意味着多边形P的全部顶点均位于直线的同一侧,说明直线与多边形P不相交,p0在多边形P的外部,协议结束.若R中的元素不全部为1 或–1,则说明直线与多边形相交,即|ICross|=0.ICross中的直线与直线相交,以点p0和ICross中的直线作为输入执行协议1,根据执行结果可以推测出直线与多边形P相交的点数,即点p0的同侧点的个数.基于5.1.1的证明可以保证该同侧点的个数的正确性.根据获得的同侧点的个数,基于定理1可以推断出点p0是在多边形P的内部还是外部.同侧点个数的正确性及文献[18]对定理1的证明可以保证推断结论的正确性. 下面讨论点在多边形上的特殊情况,点在多边形任意一条边上被认定为点在多边形内.不妨假设点p0位于直线∈ICross上,根据定义1可知=0,以点p0与直线为输入执行协议1,基于5.1.1的证明可知协议1的输出结果为0,根据协议2,因为∃0 ∈R′,所以点p0在多边形P内,协议2的输出结果是正确的. 5.2.1 协议1安全性证明 g1表示执行协议1后点的拥有者的结果,表示执行协议1后直线的拥有者的结果. 构造模拟器S1模拟直线的拥有者的协议执行过程,构造模拟器S1随机选取使得 构造模拟器S1使用自己的公钥进行如下加密操作: 构造模拟器S1选择随机数r′(r′=0,1),进行如下计算: 模拟结束. 显然,我们可以得到: 构造模拟器S2模拟点的拥有者的执行过程.构造模拟器S2随机选取其中使得 构造模拟器S2使用公钥进行如下加密操作: 构造模拟器S2选择随机数r∗(r∗=0,1),计算: 模拟结束. 显然,可以得到 上述证明过程说明协议1是隐私保护安全的. 5.2.2 协议2的安全性证明 协议2安全性要求,Alice和Bob 执行完协议2后,Alice 在不泄漏自己拥有的点p0信息和Bob 在不泄漏自己拥有多边形P的信息的情况下,Alice和Bob 均知道点p0与多边形P的相对位置关系.协议2的安全性依赖协议1.协议2的输出结果为f(p0,P)=f1(p0,P)=f2(p0,P),其中f1(p0,P)表示执行协议2后Alice 得到的结果,f2(p0,P)表示执行协议2后Bob 得到的结果.构造模拟器S3模拟Bob 执行协议2的过程,模拟器S3随机选取一个点依次以直线和多边形P的每个顶点为输入执行协议1,得到P的每个顶点与直线的位置关系集合R∗.根据R∗中的结果计算出使用中的线段执行协议1,得到结果 同理对Alice 也可以构造模拟器S4证明view4(p0,P)与S4(p∗0,P)不可区分.上述证明过程说明协议保证了双方输入信息的安全. 制约安全多方计算协议性能的主要因素是协议的通信复杂度和计算复杂度.本文将从上述两个方面对协议1和文献[14]提出的协议进行分析比较.为了便于叙述,本文分别用符号Tenc、Tdec、Tmult和Tpow表示1 次加密操作、1 次解密操作、1 次密文乘法运算和1 次模幂运算的时间. 执行1 次协议1需要进行7 次加密操作、3 次解密操作、3 次密文乘法运算和4 次模幂运算,故执行1 次协议1的计算开销为:7Tenc+3Tdec+3Tmult+4Tpow. 文献[14]利用云环境中的点积协议设计了一种点与直线关系的判定协议,在计算内积时文献[14]利用了BGN 的乘法同态,需要执行多次双线性对运算,因此本文提出的协议在计算性能方面优于文献[14]提出的协议.为了证实这一分析结果,我们给出了仿真实验.实验环境为Windows 7 64 位操作系统、内存4 G、Intel(R)Pentium(R)CPU G3220@ 3.00 GHz,基于JPBC[19]的库函数,实验模拟了协议1的执行,在模拟的过程中我们忽略了通信消耗的时间并取τ为160 bit,实验数据如表1 所示. 表1 协议1计算性能比较的实验数据(单位:ms)Table 1 Experimental data of computation performance comparison of Protocol 1(ms) 上述实验仿真数据说明本文提出的协议1的计算性能优于文献[14]提出的协议.值得注意的是,文献[20]使用的是仰角比较协议,文献[13]使用的是安全叉积协议,文献[21]使用的是极角比较协议,文献[22]使用的是角度旋转协议.协议1对比其他文献,协议1在设计上避免使用复杂的密码原语从而降低了计算开销,更加精简. 协议2的计算开销依赖于协议1的计算开销、多边形P的顶点数n以及多边形P与直线相交的边数|ICross| 表2 协议2的性能比较Table 2 Performance analysis of Protocol 2 隐私保护的点与任意多边形关系的判定问题,具有较高的研究意义.解决该问题的方法一般从问题本身出发寻找突破口,然后结合隐私保护相关技术设计具体的解决方案.本文基于支持符号位的编码和同态加密算法设计了高效的点与直线关系判定协议,然后利用模拟射线法的转化方法将点与任意多边形位置关系的判定问题转化为任意一条过点的射线与多边形相交点数的奇偶性判定问题,最后给出了具有隐私保护的点与任意多边形关系判定方案.本文研究的问题是基于半诚实模型下两个参与者的二维空间安全几何计算问题.但是如何实现三维空间下多个参与者以及恶意模型下的具有隐私保护的几何计算问题还有待进一步的研究.
5 正确性及安全性证明
5.1 正确性


5.2 安全性证明

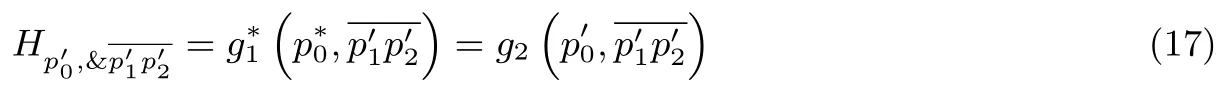
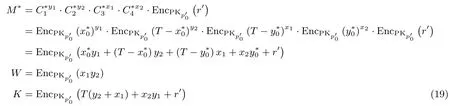






6 性能分析
6.1 协议1性能分析

6.2 协议2性能分析

7 结论

