多级维纳滤波器的快速实现方法研究

宋 佳，张 恒

(中国船舶重工集团公司第七二三研究所，江苏 扬州 225101)

0 引 言

Goldstein提出的多级维纳滤波器(MSWF)推广了传统维纳滤波器(WF)结构，其结构由一个分界滤波器组和一个合成滤波器组成，具有更强的降维能力。多级维纳滤波器是近年发展起来的降维自适应滤波技术，在很多领域都有广泛的应用，例如空时自适应雷达中的恒虚警率(CFAR)检测、自适应均衡、超分辨率谱估计等。本文研究多级维纳滤波器的快速实现方法，提出了降秩多级维纳滤波器和相关相减算法的多级维纳滤波器，并对2种滤波器进行计算机仿真实现，结果表明，多级维纳滤波器的快速实现方法保持了与经典算法几乎相同的性能，且计算量更低。

1 多级维纳滤波器基本原理

(1)

WX0称为维纳解，其中隐含这样的事实：X0(k)和d0(k)只能对消掉彼此相关的信号分量。如果X0(k)和d0(k)互不相关，则不能达到自适应滤波的目的。

图1 维纳滤波器的结构

用广义旁瓣相消的形式替换图1的下支路即得维纳滤波器的广义旁瓣相消形式，如图2所示。

图2 维纳滤波器的等效广义旁瓣相消形式

对图2中的虚线部分进一步进行等效，以此类推，直到经N-1次等效，由正交投影得到xN-1=BN-1XN-1为标量为止，取N=4时，多级维纳滤波器形式如图3所示。

图3 多级维纳滤波器(MWF)

多级维纳滤波器的处理分为2步：

(1) 对Xi(k)进行正交投影，其中Bihi=0，分解得到Xi+1(k)和参考信号di+1(k)，以此递推，使数据的维数降低至标量。

(2) 综合步骤(1)中的标量维纳滤波器，得到输出误差信号ε0(k)。

其中步骤(1)被称为前向分解，步骤(2)则被称为后项综合。由图3可以推出多级维纳滤波器的等效自适应权矢量：

(2)

(3)

(4)

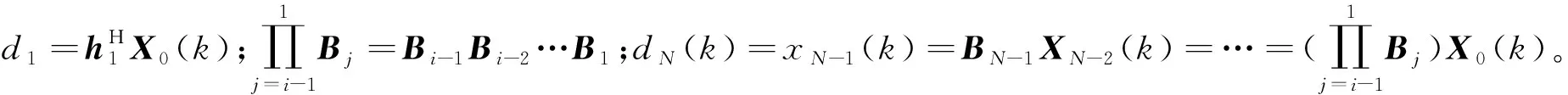
(5)

代入式(2)，可得：

(6)

则多级维纳滤波器的等效自适应权矢量为：

WMWF=WX0=LHWd

(7)

由上式可以看出，多级维纳滤波器可以等效为如图4所示的结构。

图4 多级维纳滤波器的变换域形式

图4中：

(8)

Rd=E[d(k)dH(k)]=LRX0LH

(9)

rdd0=E[d(k)d*(k)]=LrX0d0

(10)

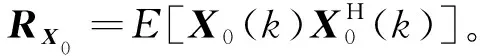
如果图3中的X0(k)和d0(k)是通过一级正交分解得到的，并且2个正交分量分别为B0和h0，即得到广义旁瓣相消器的多级维纳滤波器形式。由于广义旁瓣相消器与最小方差无失真响应(约束)波束形成器等效，因此可以成为无失真响应多级维纳滤波器(DR-MWF)[1-2]。

(11)

2 低运算量的多级维纳滤波器

2.1 降秩多级维纳滤波器

降秩多级维纳滤波器(RR-MWF)，也可称为截断多级维纳滤波器，即在第r级分解处令dr(k)=εr(k)，由图3可知：

(12)

d(k)=[d1(k),d2(k),…,dr(k)]T

(13)

(14)

(15)

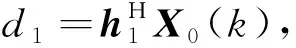
(16)

(17)

将式(16)代入(12)，可得：

(18)

等效降秩变换矩阵Tr的列向量依次为满秩时等效变换矩阵T(=LH)的前r列，即多级维纳滤波器权值WMWF位于LH张成的子空间。由于多级维纳滤波器是根据相关的强弱将输入数据向量X0(k)通过前向递推过程依次变换为d(k)，而后向递推相当于将d(k)的元素进行Gram-Schmidt正交化。因此，MWF各级分解与综合对WMWF的贡献随级数的增加而降低，因此采用截断可得到较好的降秩性能[3]。

2.2 相关相减算法的多级维纳滤波器

DR-MWF中，为实现前向递推分解中观测数据向量的维数的逐次降低，构造了行数比列数少1的长方阵阻塞矩阵，而这里考虑用归一化参考向量求取阻塞矩阵，而不再计算(构造)阻塞矩阵，从而使归一化参考向量相互正交，以提高性能和降低计算量。多级维纳滤波器可以用如图5所示的相关相减算法结构实现，称为相关相减算法多级维纳滤波器(CSA-MWF)。由于不需要求解阻塞矩阵，计算量可得到降低，而且CSA-MWF是酉多级维纳滤波器[4]，即子空间基向量相互正交，较DR-MWF(子空间基向量不正交)稳健性要好。

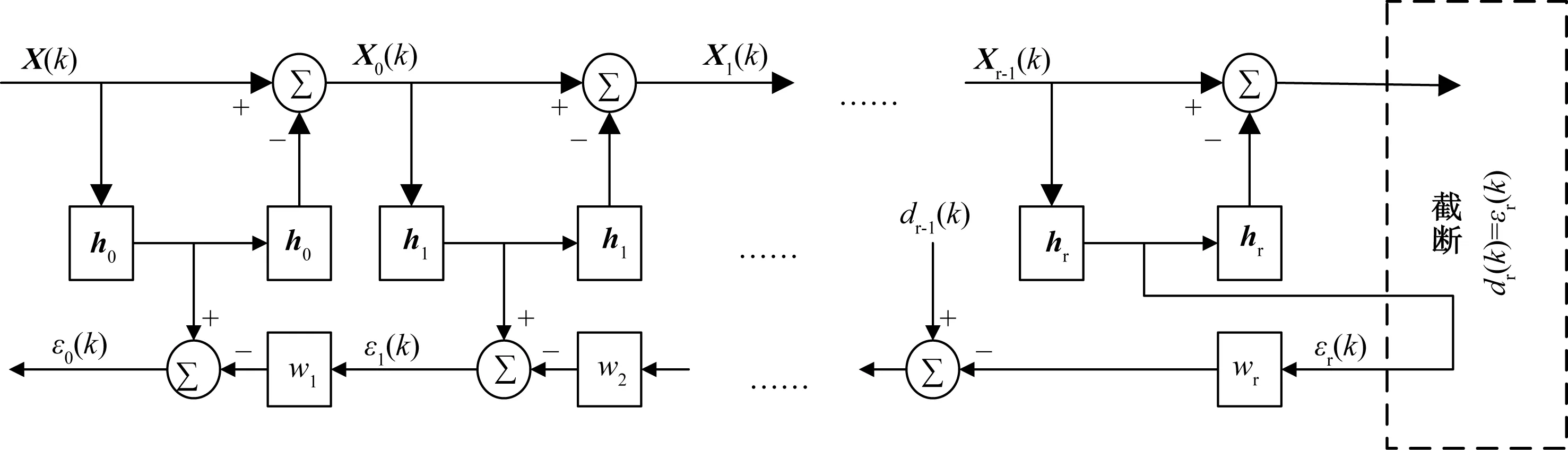
图5 多级维纳滤波器的CSA实现结构(CSA-MWF)

图5中:

X0(k)=B0X(k)

(19)

(20)

(21)

(22)

则有:

(23)

相关相减多级维纳滤波器中，第i级的前向迭代关系为:

(24)

(25)

(26)

Xi(k)=BiXi-1(k)

(27)

在相关相减多级维纳滤波器中，阻塞矩阵Bi均为N维方阵，各级观测数据Xi(k)也均为N维方阵，由CSA-MWF的原理可知，降秩处理并没有导致维数的降低[5-6]，因此数据冗余量很大。若将阻塞矩阵采用(N-i-1)×(N-i)长方阵，既利用CSA-MWF的CSA结构，不需要求解阻塞矩阵，又利用了DR-MWF降维的优点，使得Xi(k)的维数逐次降低。将这种结构称为改进的相关相减算法多级维纳滤波器(MCSA-MWF)，结构如图6所示，它综合了DR-MWF和CSA-MWF的优点，计算量比两者都小[6]。

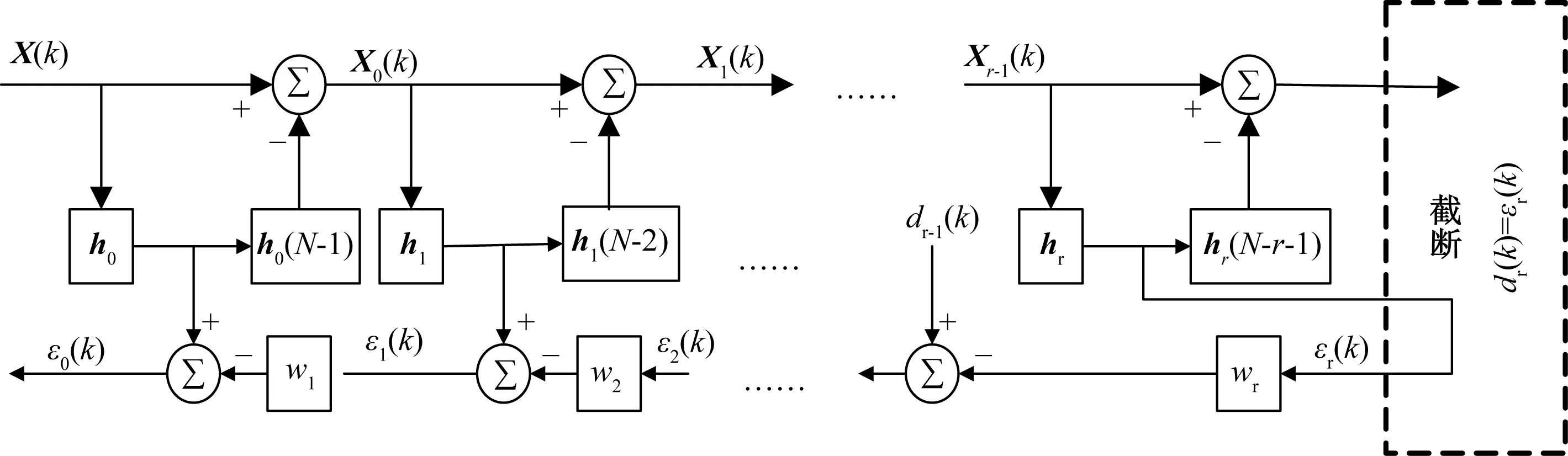
图6 改进的多级维纳滤波器CSA(MCSA-MWF)实现结构

其中

(28)

(29)

(30)

(31)

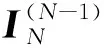
(32)

(33)

(34)

(35)

式中：hi为N-i维；Xi(k)为(N-i-1)维向量，随着级数i的增加，Xi(k)维数逐渐降低[7]。

3 算法仿真与比较

3.1 降秩多级维纳滤波器算法仿真实现

仿真条件：等间隔直线阵，阵元个数为16个，阵元间隔为半波长，幅度为1的期望信号在0°方向，3个干扰方位分别为-35°，19°，45°，干扰幅度分别为5，3，1。对降秩的DR-MWF和满秩处理2种算法波束形成和方向图仿真如图7所示。并对不同截断级数的情况进行了仿真对比，如图8所示。

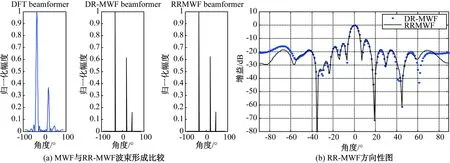
图7 RR-MWF波束形成算法计算机仿真(r=12)

从图7(b)可以看到，降秩的DR-MWF和满秩处理的方向性图相比，边缘角度的旁瓣较高，但对算法性能的影响可接受。

为了说明不同的降秩阶数和不同快拍数下降秩对性能的影响，选取不同的降秩阶数，以及不同的快拍数进行计算机仿真。

图8 不同截断级数计算机仿真结果(r=5，K=256)

从图8(a)中结果可以看到，在-35°处已有旁瓣泄漏，且主波束宽度较MWF要大，对抑制旁瓣泄漏已经有了较为明显的不足。从图8(b)中可以看到，RR-MWF的主波束较MWF有明显展宽，主瓣附近旁瓣也较高，因此截断级数过多是不可取的。说明截断会导致波束形成性能的下降，因此在使用时应当选择适当的降秩阶数，将误差控制在可以接受的范围内。

从图9(a)可以看到，降秩导致主波束的能量泄漏，会造成隧道效应。从图9(b)可知，在K=16时，MWF的方向性图已经严重畸变，而RR-MWF(r=5)可以在干扰方向形成零陷，有效抑制干扰。

图9 不同快拍数RR-MWF计算机仿真结果(r=5，K=16)

根据以上的仿真结果可知，随着降秩阶数减少或者快拍数减小，RR-MWF的性能都会下降。应根据实际应用情况，综合考虑算法性能和运算量对降秩阶数和快拍数进行选择。

3.2 相关相减算法的多级维纳滤波器仿真实现

仿真条件：等间隔直线阵，阵元个数为16个，K=256，阵元间隔为半波长，幅度1的期望信号在0°方向，3个干扰方位分别为-35°，19°，45°，干扰幅度分别为5，3，1。

如图10 (a)所示，CSA-MWF和DR-MWF波束形成算法较常规波束形成算法均能完全抑制旁瓣干扰，抑制频谱泄漏。如图10 (b)所示，CSA-MWF与MCSA-MWF均可以在干扰方向形成深的零陷。

当快拍数降低时，如图11，快拍数为K=16，CSA-MWF和MCSA-MWF的方向图近似一致，性能均优于DR-MWF，DR-MWF的旁瓣较高，这是因为DR-MWF的空间基向量无相互正交性；由于进行了10 dB的对角加载，干扰方向零陷明显变浅。

图10 相关相减算法多级维纳滤波器波束形成计算机仿真

图11 CSA-MWF、MCSA-MWF与DR-MWF仿真比较(K=16)

4 结束语

本文研究多级维纳滤波器的快速、有效实现方法，从理论分析和算法仿真2个方面进行分析，讨论了降秩多级维纳滤波器(RR-MWF)的性能与降秩阶数和快拍选择的关系，得出结论：随着降秩阶数减少或者快拍数减小，RR-MWF的性能都会下降，应根据实际应用情况，综合考虑算法性能和运算量对降秩阶数和快拍数进行选择；比较了相关相减算法的多级维纳滤波器(CSA-MWF)和改进后的相关相减算法多级维纳滤波器(MCSA-MWF)与无失真响应多级维纳滤波器(DR-MWF)快拍数降低时的性能，得出结论：CSA-MWF和MCSA-MWF的旁瓣抑制能力均优于DR-MWF，且MCSA-MWF具有更小的运算量。