一种优化MIMO雷达波形设计的算法

李 旭，安 涛，刘金鹏

(中国船舶重工集团公司第七二三研究所，江苏 扬州 225101)

0 引 言

多输入多输出(MIMO)雷达正交波形既要求雷达波形信号之间低的互相关性，又要求雷达信号具有低的自相关旁瓣。通过合理的算法优化雷达发射波形，使其具有优异的自相关和互相关特性，这样的雷达信号能够更方便地对其进行脉冲压缩，从而更好地从雷达目标回波中提取独立的速度、距离、方位等目标信息。此外，因为MIMO雷达正交信号间互相关性低，所以在不同发射方向上的功率增益远小于相同发射功率下其在波束指向上的功率增益，因此降低了雷达信号被敌方交叉定位的概率，从而提高了雷达的战场生存能力[1]。本文将对MIMO雷达相位编码信号的正交波形设计算法展开研究。

1 MIMO雷达相位编码信号模型

MIMO雷达探测目标时需要发射正交信号。为了提高雷达的探测距离和探测精度，要求MIMO雷达单个发射单元发射信号的自相关函数旁瓣尽可能低；同时多个发射单元发射信号间互相关电平[2-3]尽可能低，从而能够有效降低多目标回波间的相互干扰。

相位编码脉冲信号是雷达常用的信号形式之一，该信号通过非线性相位调制使得其相位变为离散的有限序列，因此相位编码信号是一种离散脉冲编码信号[3]。相位编码信号与线性调频(LFM)信号类似，大量的子脉冲构成相位编码的脉冲波形，且每个子脉冲具有相同的持续时间，相邻的子脉冲之间存在着相位差，如果相位差为0或π，那么形成的就是二相编码脉冲波形；如果相邻子脉冲的相位差存在2个以上的不同值，则形成多相编码脉冲波形。

假定MIMO雷达系统包含L个发射单元，每个发射单元发送相位编码信号的码元长度为N。则该相位编码信号的数学表达式为：

X={xl(n)=ejφl(n)}

(1)

式中：n=1，2，…，N；l=1，2，…，L；xl为第l个单元发射的信号；φl(n)为第l个单元发射信号的第n个码元对应的相位。

令相位编码信号的总相位数为M，则该信号的相位包含于集合(2)：

(2)

信号xp和xq的相关函数定义为：

(3)

式中：*表示复共轭。

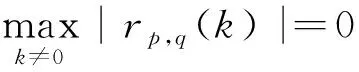
2 基于CAN算法的相位编码信号设计

雷达系统中，自相关函数旁瓣较低的雷达信号有利于检测到弱目标，互相关性低的信号可以减少其它无用信号的干扰[4]。低自相关函数旁瓣的相位编码信号需要通过专门的算法优化才能实现。发射具有低自相关旁瓣信号，并且与匹配滤波器相连时，可以明显提高雷达系统的信噪比。

减小信号自相关函数的旁瓣即使{r(k)}k≠0最小，积分旁瓣电平(ISL)的定义如下：

(4)

我们的目标是设计高效的算法将ISL最小化，ISL指标最小等价于代价因子(MF)最大，ISL与MF的关系式如下：

(5)

ISL与MF关系式的推广被称为最小权重(WISL)和最大代价因子(MMF)，其中：

(6)

(7)

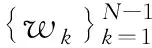
这种最小权重公式对于减少确定的多径干扰和离散杂波十分重要。

下面介绍用于减小ISL的循环算法：CAN算法。

CAN算法的推导包含几个步骤，首先已知ISL的频域表达式为：

(8)

式中：ω∈[0，2π]。

另外，由帕塞瓦尔定理式知式(4)等价于：

(9)

{ωp}应满足以下条件：

(10)

通过实验研究发现CAN算法可以减小信号的ISL指标。CAN算法是基于快速傅里叶变换(FFT)的操作，可以运用在N高达106甚至更大的序列中。

CAN算法的实现步骤如下：

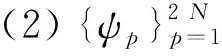
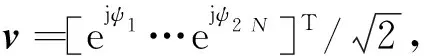
(4) 不断地迭代步骤(2)、(3)，直到满足预设的一个停止标准。比如设置‖x(i)-x(i+1)‖<ε，其中x(i)是序列进行第i次迭代后的值，ε是预先设定的停止阈值，比如ε=10-3等。

图1(a)是未经CAN算法优化的原始相位编码信号的自相关函数仿真结果，(b)是经过CAN算法优化后相位编码信号的自相关函数仿真结果。通过对比可知，经CAN算法优化后的旁瓣值明显降低10 dB。上面描述的CAN算法存在一个限制条件，即序列{x(n)}是单位弹性模量，也就是说它的峰值与平均功率的比值是1。如果该比值大于1的话，则会更好地抑制相关函数旁瓣。通过CAN算法优化后的相位编码(PC)信号可以有效提高雷达的探测性能，并且可以增强雷达信号的通用性。

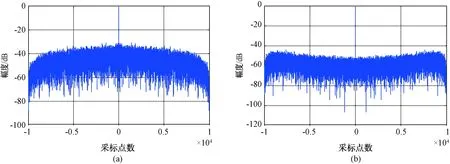
图1 相位编码信号CAN算法优化前后效果对比图

3 基于Multi-CAN算法的MIMO雷达相位编码信号设计

CAN算法是针对单一序列提高其自相关函数性能的算法，但是对于MIMO雷达发射的多通道正交波形，由于信号的多普勒敏感特性[6]，需要对波形的互相关性进行设计研究。好的自相关性能表明该波形与其经时间延迟后的波形是不相关的，而好的互相关则是任何一个具有时间延迟的波形基本上与其它波形不相关。低互相关特性可以减小多路径干扰以及杂波干扰的危险。针对MIMO雷达的特点，提出了高效率的能降低编码互相关旁瓣的Multi-CAN算法。

Multi-CAN算法的主要目的是减小式(12)中ε的值：

(11)

为了方便讨论，将发射波形的矩阵定义为：

X=[x1x2…xM]N×M

(12)

其中第m个波形：

xm=[xm(1)xm(2) …xm(N)]T

(13)

不同延迟条件下波形协方差矩阵的表达式如下：

n=-N+1，…，0，…，N-1

(14)

通过下面的转移矩阵：

(15)

式(15)可以变换为：

(16)

通过以上变换，式(12)可以被改写成：

(17)

根据帕瑟瓦尔定理得：

(18)

其中：

(19)

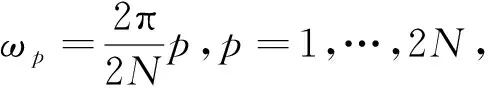
(20)

其中：

(21)

y(n)=[x1(n)x2(n) …xM(n)]T

(22)

通过式(18)和式(20)，式(17)可以变换为：

(23)

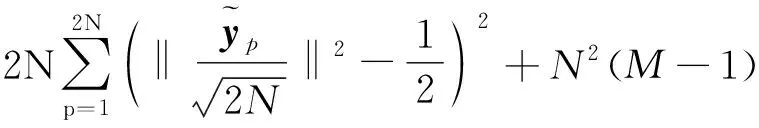
(24)

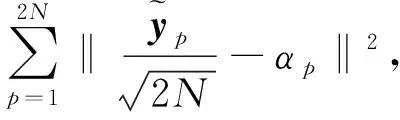
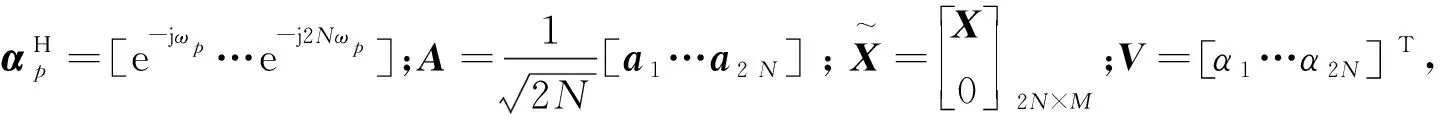
(25)

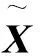
(26)

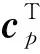
{xm(n)}=exp(jarg(dnm))

(27)

式中：m=1，…，M；n=1，…，N；dnm为AV中位于(n，m)处的元素。

因此，Multi-CAN算法的实现步骤如下：

(1) 用已经存在的拥有良好性能的序列或者随机产生的M×N序列来初始化M；

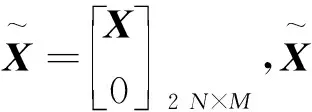
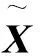
(4) 不断重复步骤(2)、(3)直到满足预设阀值条件。比如设置|x(i)-x(i+1)‖<10-3，其中x(i)是序列进行第i次迭代后的值。

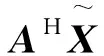
我们用Multi-CAN算法设计四组正交波形，码长为103，图2为4个信号归一化后自相关的幅值，图3是4个信号两两互相关的归一化幅值。可以看出，经过Multi-CAN算法以后，4个信号的自相关函数主峰很大、旁瓣很低，并且互相关函数没有主峰，说明Multi-CAN算法优化后组合信号间基本没有相关性。

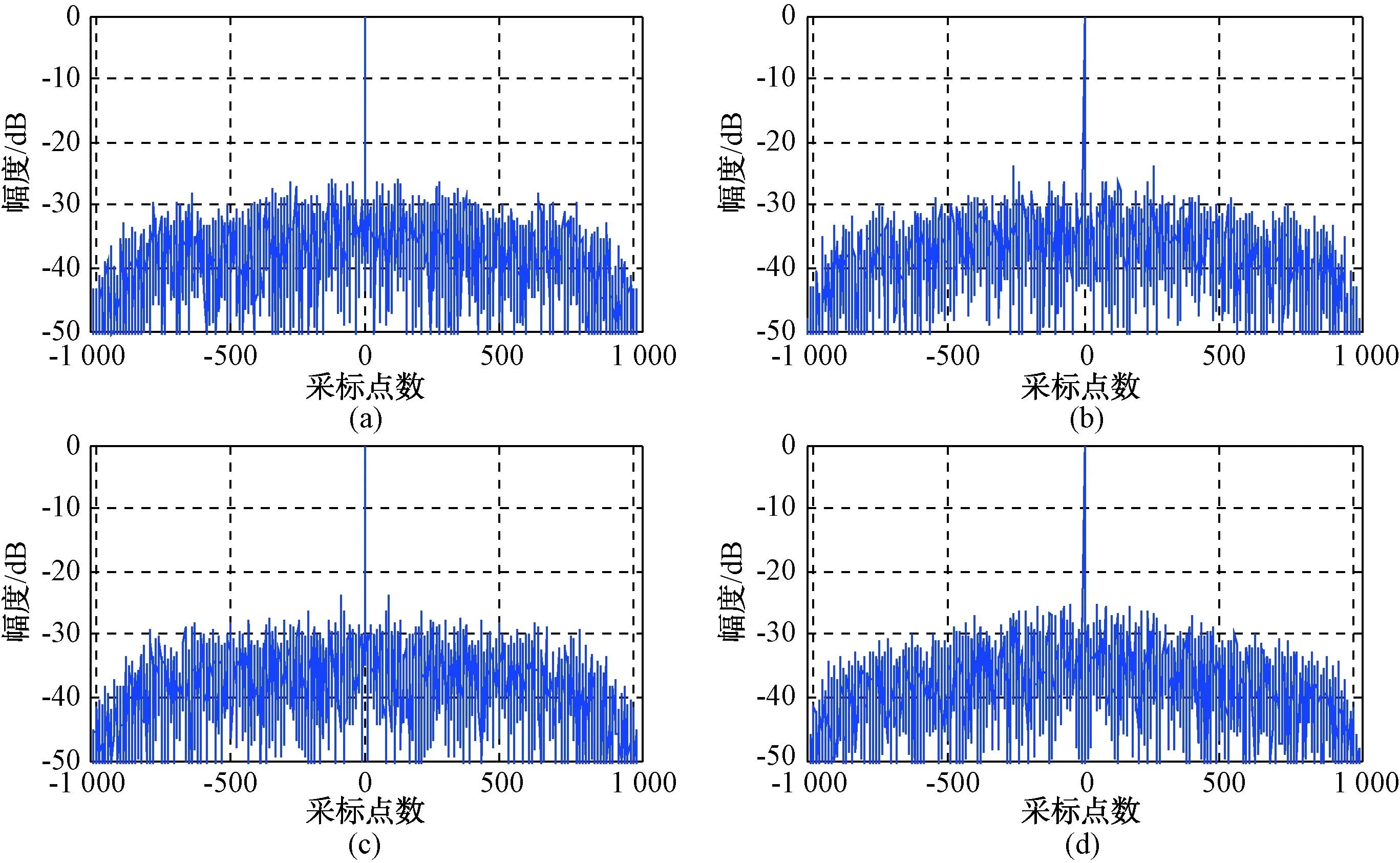
图2 4个信号的自相关性

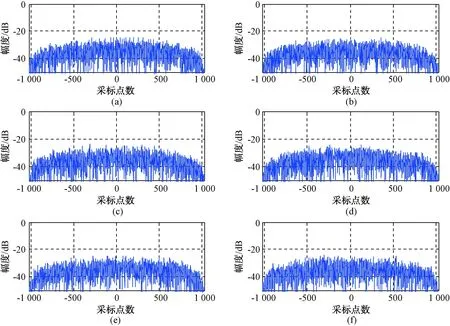
图3 4个信号两两互相关性

4 结束语

MIMO雷达在体制上的巨大优势决定了其广阔的应用前景[7]，本文研究了同时优化MIMO雷达相位编码信号自相关与互相关性的方法。CAN算法是针对单一序列提高其自相关函数性能的算法，针对MIMO雷达的特点，提出了高效率的能降低编码互相关旁瓣的Multi-CAN算法。