基于维纳滤波的超声增强实现方法
沈希忠 叶秋泽
(上海应用技术大学电气与电子工程学院,上海,201418)
引 言
超声在传播时,由于受到材质不均匀、材料内部杂质等的影响而使接受回波信号受到噪声的干扰,有时这种干扰会淹没所检测的裂纹信号,因此必须经过增强处理[1-3]。超声增强的目的就是从带噪信号中恢复原始的超声接收信号,提高信噪比,其应用十分广泛,如超声检测、超声成像[4]等。超声接收信号中噪声干扰丰富,如高斯噪声、背景噪声等,文献[1]提出了主元分析法减弱由于多途而产生的背景噪声,但超声增强与声学信号增强一样,超声接收信号的增强方法有很多,如小波方法、卡尔曼滤波和MMSE等,本文重点探讨谱减法[5]和维纳滤波法[6],其中维纳滤波是基于最小均方误差准则下构造的一种滤波器[4]。其中维纳滤波的应用非常广泛,如在图像处理上的应用。另外,还可以从伪影的角度探讨噪声抑制,如文献[7]提出空间位移复合方法校正位移估计,从而抑制伪影噪声。超声增强方法大都用到短时谱估计,传统的短时谱估计的方法存在着残留噪声大的问题,如谱减法存在“音乐噪声”问题。为此,有学者提出了有效地抑制残留噪声的方法,如Ephriam和Malah方法[8]、Israel Cohen[9]的改进方法和Scalart[10]。本文总结了维纳滤波原理,并将维纳滤波应用于超声回波信号的增强,提出具体的应用方法和流程图,解决信噪比自适应估计的具体方案,分析比较在不同信噪比下的维纳滤波效果,并与谱减法去噪效果进行比较。
1 超声回波信号模型

图1 材料裂纹的超声检测Fig.1 Ultrasonic detection of material crack
在超声检测材料裂纹时,如图1所示,超声传感器Tx发射一个超声波信号,超声信号在材料空间(由边缘B,T,L,R构成)传播时遇到裂纹(图中标注为Flaw)而发生反射等声学现象,被传感器Rx接收的信号为
r(t)=βs(t-τ)
(1)
式中:β为超声信号在传播过程中的衰减因子,τ为接收信号的延迟时间。
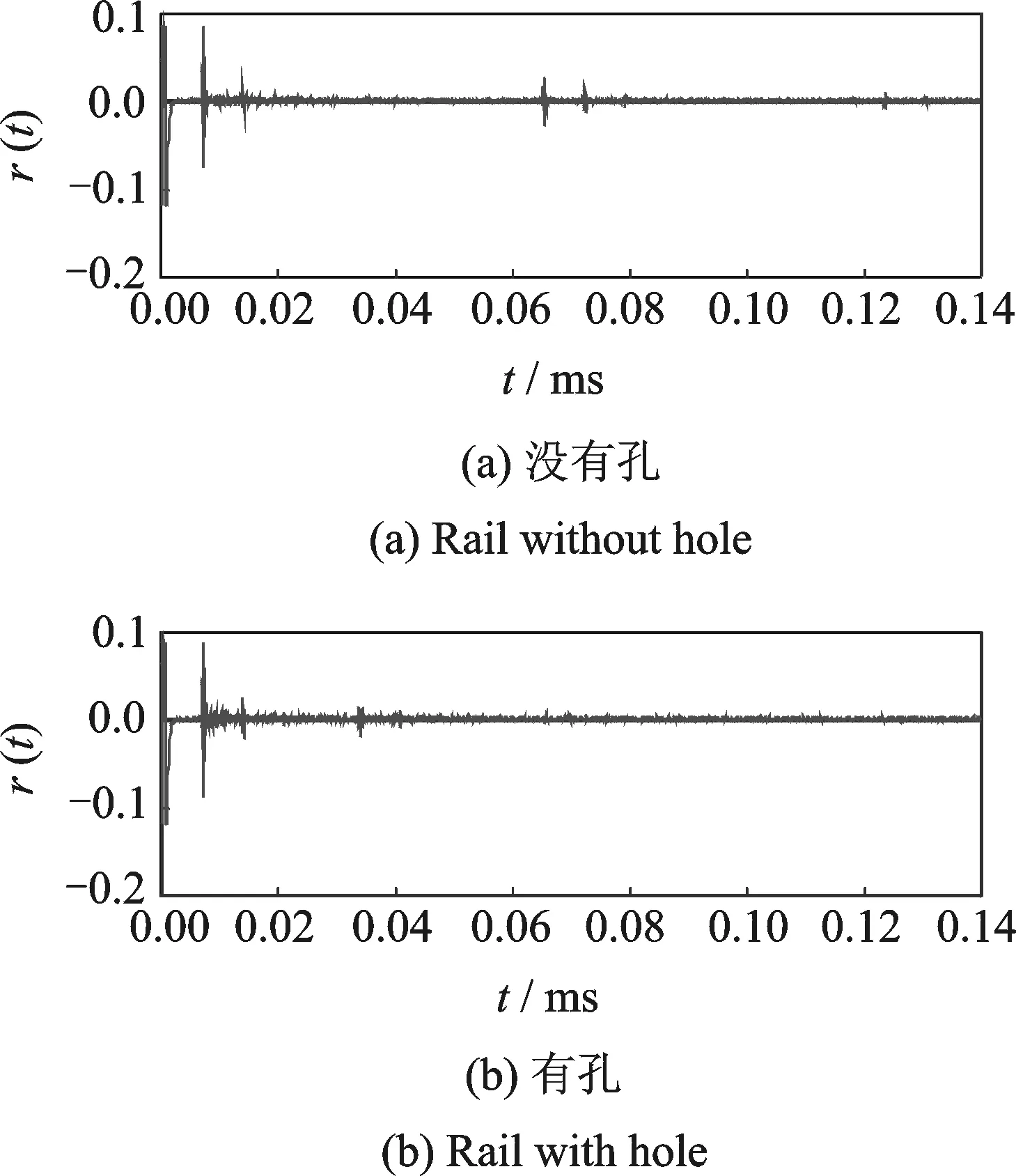
图2 测铁轨裂纹的超声信号Fig.2 Ultrasonic echo of railroad rail
超声在传播过程中,不可避免地受到多种因素的影响而呈现复杂多变的噪声干扰。如材料界面的影响,超声在上下表面会形成很强的反射波,如果裂纹离界面很近,这种发射波会淹没裂纹信号,文献[1]重点研究了如何去除这种干扰。又如材料内部材质的不均匀和杂质的影响,超声在传播过程中当遇到此类情况可能呈现复杂多变的反射、绕射和衍射等声学现象,一般很难具体用数学公式来说明,但可以用统计的方法加以描述。另外,传感器在发射和接收过程中存在一定的电子干扰噪声,还有材料表面不可避免存在一定的粗造度,使得超声信号在发射和接收时收到表面凹凸的影响而呈现一定衰减和延迟现象,所有这些现象使得接收信号呈现随机噪声的特点。
被测超声信号rm(t)是平稳随机干扰噪声信号n(t),并叠加有发射信号β0s(t-τ0)、表面反射信号βWs(t-τW)和缺陷的反射信号βFs(t-τF)等,式(1)可以修改为
(2)
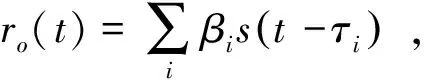
2 维纳滤波
2.1 维纳滤波原理
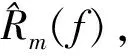
(3)
式中E为期望均值。通过求导求驻点,可以求得式(3)的最佳值W(f),即最小均方误差维纳滤波器[8]为
(4)
式中:PRR(f)=E[Rm(f)Rm*(f)];PSR(f)=E[Ro(f)Rm*(f)];Ro(f)为ro(t)的傅里叶变换。由于噪声信号与反射信号统计独立,因此PSR(f)=E[Ro(f)Ro*(f)]=PSS(f),同样地,PRR(f)=PSS(f)+PNN(f),PNN(f)=E[N(f)N*(f)],N(f)为n(t)的傅里叶变换,代入式(4),有[4]
(5)
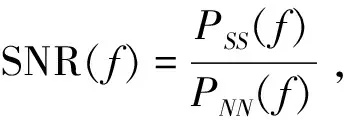
(6)
可见,超声信号的维纳滤波可以用信噪比表示(此处定义与下文用dB表示的信噪比不同),问题的关键在于如何估计此信噪比。
2.2 信噪比估计
由式(6)可知,维纳滤波的关键是信噪比的估计。假设所检测的材质是均匀的,那么超声接收信号的噪声是平稳随机信号,其功率估计比较简单,但由于受到其他如材料块中的孔反射、表面反射等的影响,所以具体处理时必须加以剔除,也就是噪声估计时必须首先判断有无超声反射,如果是反射波则进行维纳滤波,如果是噪声则用于信噪比的估计。与语音信噪比[8]估计一样,首先设定一个噪声阈值vthreshold。并计算
如果vthreshold,即判断为噪声段,则估计后验信噪比
然后计算先验信噪比为
(7)
否则,判断为存在反射波,利用式(6)进行维纳滤波。

图3 超声回波的包络线与初始噪声判断Fig.3 Envelope of ultrasonic echo with initial decision of noise
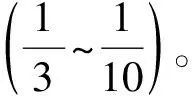
由式(7)可见,噪声功率谱PNN(f)在维纳滤波中很重要。为了自适应地计算PNN(f),先对被测回波rm(t)作Hilbert变换求出其包络,如图3所示,点线为原回波信号,蓝线为其包络,水平绿线为设置噪声的判断值,其值以下假设为噪声干扰,大于此判断值为脉冲。然后再对所有噪声段的功率谱分段统计平均,并设为初始噪声功率PNN,0(f),则自适应计算噪声段功率谱为
PNN(f)=βPNN,c(f)+(1-β)PNN,0(f)
(8)
式中:PNN,c(f)为当前噪声段的功率谱,β为用于噪声段功率谱估计的自适应加权系数,一般取0.5~0.9,本文取0.9。
2.3 超声维纳滤波实现
利用维纳滤波进行超声信号增强实现如图4所示,超声信号因反射而叠加的超声小波使其呈现短时平稳特性,因此需要分帧处理,一般每帧长度近似为1~20 μs,同时加窗也使得信号频谱具有较好的局部特性,常用的由Hamming窗。与分帧、加窗和FFT对应的逆变换有IFFT、重叠相加和去窗口效应。框图中的维纳滤波和信号比估计分别见式(6,7)。

图4 超声信号的维纳滤波Fig.4 Wiener filter of echo
3 超声实测验证
为了获得维纳滤波对超声回波信号的滤波效果,作者设计了一段铁轨,并加工有一孔作为裂纹。由于现场平均处理比较耗时,因此考虑直接获取回波信号,而不进行平均,但这样获取的回波难以计算其信噪比。为此,采集回波时对信号进行了32次平均,并作为干净的信号,采样频率为40 MHz,然后分别叠加高斯噪声,叠加后的回波信噪比(定义为10log(PSS(f)/PNN(f)))分别为5,6,6.5,7,7.5,8和8.5 dB,滤波所用分帧长度64点,为1.6 s,采用矩形窗(也可以用其他窗函数,如Hanning窗等,其效果类似),噪声阈值vthreshold具体见表1。为了说明维纳滤波在超声回波上的效果,与谱减法[9]相比,下面表格和图例同时给出维纳滤波与谱减法的去噪效果。

表1 维纳滤波前后的信噪比
图5为实测超声回波信号维纳滤波前后的比较,维纳滤波后信噪比由原7 dB提升到24.10 dB,信噪比提高了17 dB,而谱减法后的信噪比为8.34 dB。

图5 超声回波的维纳滤波的比较Fig.5 Comparison of the Wiener filtering and spectral subtraction
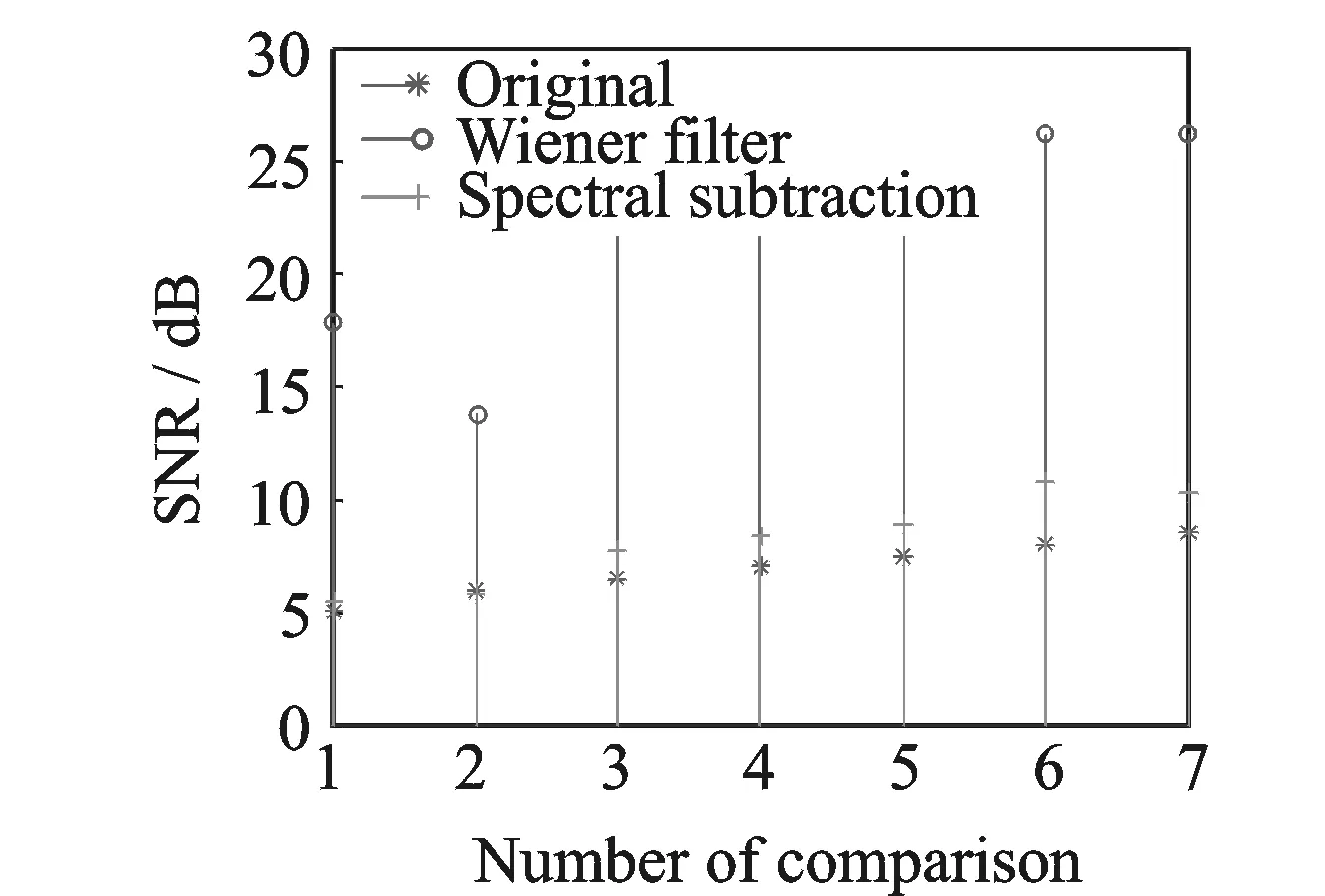
图6 维纳滤波前后的信噪比Fig.6 Comparison of signal-noise-ratio before and after the Wiener filtering
图6为维纳滤波前后的信噪比比较,图中用“*”表示原始信号的信噪比,“o”表示维纳滤波后的信噪比,“+”表示谱减法去噪后的信噪比。为了获得比较好的维纳滤波效果,适当调整噪声阈值vthreshold,见表格1。其中第4点7 dB信噪比的超声回波滤波前后见图5中图所示,滤波后的信噪比见表格1。由此可见,超声回波信号经过维纳滤波后信噪比提高了,比谱减法去噪效果好。
图7为真实采集的铁轨超声检测信号,没有进行平均,图7(b)为维纳滤波后的回波,图7(c)为用谱减法获得的去噪回波,可见两种方法都使得裂纹部分(用椭圆圈注)更加清晰,维纳滤波后的图像最清晰。

图7 铁轨超声回波的维纳滤波前后信号Fig.7 Demo of the railroad ultrasonic echo
4 结束语
本文提出了维纳滤波超声增强的具体实现方法,同时给出统计平均无脉冲段的初始噪声功率谱估计方法,自适应计算噪声段功率谱,并进行维纳滤波。超声实验数据表明,维纳滤波的该实现方法在超声降噪方面比谱减法更加有效,实验中维纳滤波后信噪比提高了十几个分贝,使得裂纹信号更加清晰。
参考文献:
[1] Shen Xizhong, Zhang Y D, Amin M G. et al. Ultrasound multipath background clutter mitigation based on subspace analysis and projection [C]∥ 2012 IEEE International Conference on Acoustics, Speech, and Signal Processing (ICASSP 2012). Kyoto, Japan:[s.n.],2012: 2505-2508.
[2] 许凯亮, 张正罡, 刘丹, 等. 高分辨率超声Lamb波频散曲线测量与板厚估计[J]. 数据采集与处理, 2017, 32(2): 286-292.
Xu Kailiang, Zhang Zhenggang, Liu Dan, et al. High-resolution ultrasonic Lamb waves dispersion measurement and plate thickness evaluation [J]. Journal of Data Acquisition and Processing, 2017, 32(2): 286-292.
[3] 刘洋, 郭霞生, 章东, 等. 基于时间反转的骨裂纹超声成像模拟研究[J]. 声学学报, 2011, 36(2): 179-184.
Liu Yang, Guo xiaosheng, Zhang Dong, et al.A simulation study of ultrasonic imaging of micro-crack in bone based on time-reversed approach [J]. Acta Acoustica, 2011, 36(2): 179-184.
[4] Ramozan D, Moeness G A, Shen Xizhong, et al. Ultrasonic flaw detection and imaging through reverberant layers via subspace analysis and projection[J]. Advances in Acoustics and Vibration, 2012,2012:1-10.
[5] Karam M, Khazaal H F, Aglan H, et al. Noise removal in speech processing using spectral subtraction [J]. Journal of Signal and Information Processing, 2014, 5: 32-41.
[6] 张贤达. 现代信号处理[M]. 北京: 清华大学出版社, 2015: 163-212.
Zhang Xianda. Modern signal processing [M]. Beijing: Tsinghua University Press, 2015: 163-212.
[7] 邵党国, 钟明, 易三莉, 等. 基于空间位移复合的超声弹性成像抑噪[J].数据采集与处理, 2014, 29(1): 66-70.
Shao Dangguo, Zhong Ming, Yi Sanli, et al. Spatial displacement compounding to reduce artifact for ultrasound elastography [J]. Journal of Data Acquisition and Processing, 2014, 29(1): 66-70.
[8] Ephraim Y,Malah D.Speech enhancement using a minimum meansquare error log-spectral amplitude estimator [J]. IEEE Trans on Acoustics,Speech,Signal Processing,1985,ASSP-32:443-445.
[9] Cohen I. Speech enhancement using a noncausal a priori SNR estimator [J]. IEEE Signal Processing Letters,2004(9):725-728.
[10] Scalart P, Vieira-Filho J.Speech enhancement based on a prior signal to noise estimation[C]∥ Proceedings of the 21th IEEE International Conference on Acoustics, Speech and Processing ICASSP-96. Atlanta, Georgia:[s.n.],1996:629-632.
[11] Haykin S. Adaptive filter theory[M]. Washington: Pearson Education, 2002:198-250.

