基于MapReduce和上采样的两类非平衡大数据集成分类
翟俊海 张明阳 王陈希 刘晓萌 王耀达
(1.河北省机器学习与计算智能重点实验室,保定,071002; 2.河北大学数学与信息科学学院,保定,071002; 3.河北大学计算机科学与技术学院,保定,071002)
引 言
随着计算机网络、数据存储、云计算和社会计算等技术的快速发展,数据正以前所未有的速度在不断地增长和积累,大数据处理已经成为学术界和工业界密切关注的问题。大数据是指具有海量(Volume)、多模态(Variety)、变化速度快(Velocity)、蕴含价值高(Value)和可靠性高(Veracity)“5V”特征的数据[1-3]。目前,针对大数据分类的研究主要集中在如何处理大数据量上。解决问题的主流思路包括两种:(1)并行化或分布式方法;(2)基于采样技术的方法。在第一种方法中,由于MapReduce编程模型的盛行,大数据分类的并行化或分布式方法基本上都是基于这种编程模型而提出的。例如,Bechini等利用MapReduce编程模型对著名的关联规则挖掘算法FP-Growth进行并行化,以实现从大数据中挖掘关联规则[4]。Zhang等将深度学习和MapReduce结合起来,提出了受限波尔兹曼机的分布式学习框架[5],可实现大数据环境中的深度学习。钱宇华等对大数据关联关系度量研究进行了全面的综述[6],具有较高的参考价值。吴启晖等对面向频谱大数据处理的机器学习方法进行了总结,分析了它们各自的特点[7]。吉根林和赵斌综述了时空轨迹大数据模式挖掘与知识发现领域的研究进展[8]。亓峰等对未来大数据环境下的配用电通信网虚拟网络架构及应用进行了研究[9]。第二种方法利用采样技术从大数据集中选择一个子集代替原来的大数据集进行分类。He等利用不确定性分布,提出了一种从大数据中并行随机采样的方法[10]。与同类算法相比,该方法不仅可以保持原数据超曲面的一致性,而且可以获得非常好的加速比、伸缩比和承载比。针对大数据的Boosting集成学习问题,Dubout等提出了一种自适应采样方法[11]。该方法通过对基本分类器的统计边界行为建模,能够改进大数据Boosting集成算法的性能。文献[12]对采样方法研究进行了较全面的综述,具有一定的参考价值。
在现实生活中,很多实际问题中要处理的大数据具有类别非平衡的特点。例如,网络入侵检测、信用卡欺诈检测、恶劣天气预报和医疗诊断等问题。非平衡大数据分类使传统的分类算法面临新的挑战,如何解决非平衡大数据分类问题已成为机器学习和数据挖掘领域的研究热点。处理类别非平衡问题的常用方法大致可分为4类[13-15]:(a)数据级的方法,(b)算法级的方法,(c)代价敏感性方法,(d)集成方法。数据级的方法主要利用采样技术,包括对小类样本的随机上采样、对大类样本的随机下采样和基于数据生成的混合采样等。Japkowicz等提出了基于随机化的上采样和下采样方法[13],并从理论上证明了“在采样之后的数据集合上学习,算法能够获得与原数据集合上等效的学习性能”。Wang等针对近邻分类器给出了基于特征空间相似性的合成上采样方法SMOTE[16]。Batista等提出了基于压缩近邻规则和数据清洗技术的上采样方法[17]。2006年Liu等提出了基于集成策略的独立下采样方法[18]。算法级的方法主要利用归纳偏置、惩罚约束和调整类边界等机制对已有算法(如决策树、支持向量机等)进行改进。代表性的工作包括Quinlan提出的通过调整决策树叶结点的概率估计来选择合适的归纳偏置[19];Lin等提出的对不同类别的样例采用不同惩罚系数的支持向量机分类方法[20]等。代价敏感性方法主要利用样例加权、贝叶斯风险理论等方法设计代价敏感性学习模型。代价敏感性学习的目的是最小化标准数据挖掘或机器学习算法在训练集合上面的错分代价。研究结果表明:通过采用基于代价敏感性方法构建的神经网络[21]、支持向量机[22]和决策树[23]分别可以改善这些传统的数据挖掘和学习算法在非平衡数据集合上的学习性能。集成方法主要包括代价敏感性集成方法和基于数据预处理的集成方法。一般地,代价敏感性集成方法通过在AdaBoost算法的权更新公式中引入代价项完成,权更新规则的不同,得到了不同的代价敏感性集成方法。代表性的工作包括Fan等提出的AdaCost算法[24];Sun等提出的AdaCx(x=1,2,3)系列算法[25];Ting提出的CSBx(x=1,2)系列算法[26]等。基于数据预处理的集成方法大致又可分为3类:基于Boosting的方法、基于Bagging的方法和混合方法。基于Boosting的方法代表性的工作包括Chawla等提出的SMOTEBoost算法[27];Seiffert等提出的Rusboost算法[28]等。基于Bagging的方法代表性的工作包括Wang 等提出的OverBagging算法和UnderOverBagging算法[29];Barandela等提出的UnderBagging算法[30]等。混合算法代表性的工作包括Liu等提出的EasyEnsemble算法和BalanceCascade算法[31]。
上面这些算法都是针对中小型类别非平衡数据集提出的分类方法,对于类别非平衡的大型数据集,上述算法的效率就会变得非常低,甚至不可行。针对这一问题,在两类分类的框架下,本文提出了一种基于MapReduce和上采样的两类非平衡大数据集成分类方法,并在5个类别非平衡的大型数据集上进行了实验,实验结果证明本文提出的算法是解决两类非平衡大数据分类问题的一种有效方法。
1 基础知识
本节介绍将要用到的基础知识,包括MapReduce[32]和极限学习机(Extreme learning machine, ELM)[33]。ELM用作分类器对数据进行分类。
1.1 MapRecuce
MapRecuce[32]是针对大数据处理的一种并行编程框架,它的基本思想包括以下3个方面:
(1)MapRecuce采用分治策略自动地将大数据集划分为若干子集,并将这些子集部署到不同的云计算节点上,并行地对数据子集进行处理;
(2)基于函数编程语言LISP的思想,MapRecuce提供了两个简单易行的并行编程方法:Map和Reduce,用它们实现基本的并行计算;
(3)许多系统级的处理细节MapRecuce能自动完成,这些细节包括:
(a)计算任务的自动划分和自动部署;
(b)自动分布式存储处理的数据;
(c)处理数据和计算任务的同步;
(d)对中间处理结果数据的自动聚集和重新划分;
(e)云计算节点之间的通讯;
(f)云计算节点之间的负载均衡和性能优化;
(g)云计算节点的失效检查和恢复。
MapRecuce处理数据的流程如图1所示。

图1 MapRecuce处理数据的流程示意图Fig.1 Flow chart of data processing by MapRecuce

图2 单隐含层前馈神经网络Fig.2 Single-hidden layer feedforward neural network
1.2 极限学习机
ELM[33]是黄广斌等提出的一种训练单隐含层前馈神经网络(如图2 所示)的简单而有效的算法。ELM随机生成输入层的权值和隐含层结点的偏置,用分析的方法确定输出层的权值。与其他的单隐含层前馈神经网络训练算法相比,ELM 的优点是不需要迭代调整权参数,具有非常快的学习速度和非常好的泛化能力。而且,黄广斌等证明了ELM具有一致逼近能力[34]。
给定训练集D={(xi,yi)|xi∈Rd,yi∈Rk},1≤i≤n,具有m个隐含层结点的单隐含层前馈神经网络可表示为
(1)
式中:g(·)是激活函数;wj=(wj1,wj2,…,wjd)T是输入层结点到隐含层第j个结点的权向量;bj是隐含层第j个结点的偏置, 在ELM中wj和bj是随机生成的;βj=(βj1,βj2,…,βjm)T是隐含层第j个结点到输出层结点的权向量,βj可通过给定的训练集用最小二乘拟合来估计,βj应满足
(2)
式(2)可以写成如下的矩阵形式
Hβ=Y
(3)
其中
式中:H是单隐含层前馈神经网络的隐含层输出矩阵,它的第j列是隐含层第j个结点相对于输入x1,x2,…,xn的输出,它的第i行是隐含层相对于输入xi的输出。如果单隐含层前馈神经网络的隐含层结点个数等于样例的个数,那么矩阵H是可逆方阵。此时, 用单隐含层前馈神经网络能零误差逼近训练样例。但一般情况下,单隐含层前馈神经网络的隐含层结点个数远小于训练样例的个数。此时,H不是一个方阵, 线性系统式(3)也没有精确解, 但可以通过求解下列优化问题的最小范数最小二乘解来代替式(3)的精确解,即

(4)
上式最小范数最小二乘解可通过下式求得,即
其中H+是矩阵H的Moore-Penrose广义逆矩阵。
极限学习机算法描述如下:
算法1: 极限学习机算法
1.输入: 训练集D={(xi,yi)|xi∈Rd,yi∈Rk,1≤i≤n};激活函数g;隐含层节点数m。
3.for (j=1;i≤m;j=j+1) do
4.随机给定输入权值ωj和偏置bj;
5.end
6.计算隐含层输出矩阵H;
7.计算矩阵H的广义逆矩阵H+;
2 基于MapReduce和上采样的两类非平衡大数据集成分类

图3 在正类样例与其负类最近邻的连线上上采样若干正类样例Fig.3 Sampling of some points on the line between positive instance and its negative nearest neighbor


图4 BECIMU算法的流程图Fig.4 Flow diagram of BECIMU algorithm
算法2的第3~7步实现正类样例的上采样。其中,第4步用MapReduce寻找正类样例的异类最近邻,整个算法的计算时间复杂度主要体现在这一步。假定云平台中有m个计算节点,显然这一步的计算复杂度为O(n)/m。第5步在正类样例与其异类最近邻的连线上上采样,采样点的位置取决于参数λ,λ取不同的值可得到不同的采样点。λ的值越小,上采样点越靠近正类样例点。算法的其他步骤易于理解,不再赘述。
在算法2中,MapReduce的Map函数和Reduce函数的设计如算法3和算法4所示。在算法3和算法4中,〈k1,v1〉分别是〈起始偏移量,训练样本〉;〈k2,v2〉分别是〈vector〈欧式距离,训练样本类标志〉, NullWritable〉;〈k3,v3〉分别是〈测试样本,测试样本的类标志〉。
算法2: BECIMU算法
1.输入:两类非平衡大数据集D=S+∪S-, |S+|=n+, |S-|=n-,n+≪n-;测试样例x。
2.输出:x的类标
3.for (i=1;i≤n+;i=i+1) do
7. end
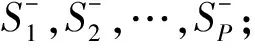
9.for (i=1;i≤p;i=i+1) do

11. 在Di上,用极限学习机算法训练一个分类器Li;
12. end
13. 用多数投票法集成p个训练好的分类器Li;
14. 用集成系统预测测试样例x的类标;
15. 输出x的类标。
算法3:Map函数
1.输出:〈k1,v1〉。
2.输出: 〈k2,v2〉
3.//遍历所有负类样例xi,取出其类标志label;
4.for(i=1;i≤n;i=i+1) do
5. label-FindLabel (xi);
6. //遍历正类样例x,计算其与负类样例之间的欧式距离,并将结果存入Context;
7. for (∀x∈testfile) do
8. Distance-EuclideanDistance(x-xi);
9. Context.write(vector〈Distance,label〉, NullWritable);
10. end
11.end
12.输出〈k2,v2〉。
算法4: Reduce函数
1.输出: 〈k2,v2〉
2.输出: 〈k3,v3〉
3. // 将vector(Distance, label)添加到Arraylist中;
4. ArrayList(Vector〈Distance, label〉);
5. //对Arraylist中所有元素执行排序操作;
6. Sort(ArrayList)
7. //将最近邻添加到result中;
8. New ArrayList result;
9. result.add(ArrayList.get(1));
10. //应用最近邻算法,结果存入Context中;
11. Context.write(x,NN(result));
12. 输出〈k3,v3〉
3 实验结果
为了验证提出的算法的有效性,在5个非平衡大数据集上进行了实验,分别与SMOTE-Vote,SMOTE-Boost和SMOTE-Bagging 3种算法[35]进行了比较。实验所用的云计算平台及各个节点的配置分别列表1和表2中。

表1 实验所用云计算平台的配置

表2 云计算平台节点的配置
实验所用的5个非平衡大数据集分别记为A,B,C,D和E。数据集A是由UCI数据集Skin_segment变换而来,包含3 679个正例和114 039个负例;数据集B由UCI数据集MiniBooNE变换而来,包含4 800个正例和196 555个负例;数据集C由UCI数据集Cod_rna变换而来,包含7 742个正例和328 168个负例;数据集D是一个人工数据集,包含150个正例和321 191个负例。数据集E是一个2类二维服从高斯分布的人工数据集,包含400万个样例。其中,正类样例所占比例为1%。两类服从的高斯分布为
p(x|ωi)~N(μi,Σi)i=1,2
(5)
其中参数如表3所示。

表3 两个高斯分布的均值向量和协方差矩阵

图5 混淆矩阵Fig.5 Confusion matrix
对于两类非平衡分类问题,设T和F分别表示实际的正类类标和负类类标,Y和N分别表示预测的正类类标和负类类标,混淆矩阵的定义如图5所示。常用的评价两类非平衡分类算法性能的指标有精度(Precision)、召回率(Recall)、几何均值(G-mean)和F-度量(F-measure),它们的定义如下。
(5)
(6)
(7)
(8)
其中β是一个参数。因为G-mean从真阳性率和假阴性率两方面度量了两类非平衡分类算法的性能,所以本文用它作为评价指标。与SMOTE-Vote,SMOTE-Boost和SMOTE-Bagging 三种算法比较的实验结果如表4所示。

表4 本文算法与3种算法比较的实验结果
在MapReduce框架下,对提出的算法还进行了加速比的比较,即对于相同的数据集在计算节点不同时速度差异,实验结果如表5所示。

表5 加速比的实验结果
从表4的实验结果可以看出,本文算法的G-mean值均高于其他3种算法。其原因是SMOTE算法仅在同类近邻的连线上采样一个样例点;而本文算法在正类样例与其异类最近邻的连线上采样多个样例点,可以扩大正类样例的学习域。从表5的实验结果可以看出,本文算法的加速比也很明显。因此,从这两方面看,本文提出的算法是比较有效的。
4 结束语
针对两类非平衡大数据分类问题,提出了一种基于MapReduce和上采样的集成分类算法。该算法利用MapReduce的并行计算机制,寻找每一个正类样例的负类最近邻,并在每一个正类样例与其异类最近邻的连线上采样若干个正类样例点,采样点的个数由用户控制,具有较强的自适应性。另外,本文提出的算法并行计算每一个正类样例到每一个负类样例的距离,极大地降低了计算时间复杂度。在5个数据集上与SMOTE-Vote,SMOTE-Boost和SMOTE-Bagging 三种同类方法进行了实验对比,实验结果证明本文提出的方法优于这3种方法。本文提出的算法具有如下两个特点:(1)算法在正类样例与其异类最近邻的连线上采样多个样例点,这样可以扩大正类样例的学习域;(2)算法具有较好的加速比和较高的分类精度。未来进一步的工作包括:(1)在更多、更大的数据集上实验,并对实验结果进行统计分析;(2)将本文提出的算法扩展到多类非平衡问题。
参考文献:
[1] Emani C K, Cullot N, Nicolle C. Understandable big data: A survey[J]. Computer Science Review, 2015,17:70-81.
[2] Zhou Z H, Chawla N V, Jin Y C, et al. Big data opportunities and challenges: Discussions from data analytics perspectives[J]. IEEE Computational Intelligence Magazine, 2014,9(4):62-74.
[3] 孟小峰, 慈祥.大数据管理:概念、技术与挑战[J].计算机研究与发展,2013,50(1):146-169.
Meng Xiaofeng, Ci Xiang. Big data management: Concepts, techniques and challenges [J]. Journal of Computer Research and Development, 2013,50(1):146-169.
[4] Bechini A, Marcelloni F, Segatori A. A MapReduce solution for associative classification of big data [J]. Information Sciences, 2016,332(1):33-55.
[5] Zhang K, Chen X W. Large-scale deep belief nets with MapReduce[J]. IEEE Access, 2014,2(2):395-403.
[6] 钱宇华, 成红红, 梁新彦,等.大数据关联关系度量研究综述[J].数据采集与处理,2015,30(6):1147-1159.
Qian Yuhua, Cheng Honghong, Liang Xinyan, et al. Review for variable association measures in big data[J]. Journal of Data Acquisition and Processing, 2015,30(6):1147-1159.
[7] 吴启晖, 邱俊飞, 丁国如.面向频谱大数据处理的机器学习方法[J].数据采集与处理,2015,30(4):703-713.
Wu Qihui, Qiu Junfei, Ding Guoru. Machine learning methods for big spectrum data processing[J]. Journal of Data Acquisition and Processing, 2015,30(4):703-713.
[8] 吉根林, 赵斌. 时空轨迹大数据模式挖掘研究进展[J]. 数据采集与处理, 2015,30(1):47-58.
Ji Genlin, Zhao Bin. Research progress in pattern mining for big spatiotemporal trajectories[J]. Journal of Data Acquisition and Processing, 2015, 30(1):47-58.
[9] 亓峰, 唐晓璇, 邢宁哲, 等.未来大数据环境下的配用电通信网虚拟网络架构及应用[J].数据采集与处理,2015, 30(3):511-518.
Qi Feng, Tang Xiaoxuan, Xing Ningzhe, et al. Virtual network architecture and application for smart distribution grid in future large data environment[J]. Journal of Data Acquisition and Processing, 2015, 30(3):511-518.
[10] He Q, Wang H, Zhuang F Z, et al. Parallel sampling from big data with uncertainty distribution[J]. Fuzzy Sets & Systems, 2015,258:117-133.
[11] Dubout C, Fleuret F. Adaptive sampling for large scale boosting [J]. Journal of Machine Learning Research, 2014, 15(2):1431-1453.
[12] 宋寿鹏, 邵勇华, 堵莹. 采样方法研究综述[J]. 数据采集与处理, 2016, 31(3):452-463.
Song Shoupeng, Shao Yonghua, Du Ying. Survey of sampling methods[J]. Journal of Data Acquisition and Processing, 2016,31(3):452-463.
[13] Japkowicz N, Stephen S. The class imbalance problem: A systematic study[J]. Intelligent Data Analysis, 2002,6(5):429- 449, 2002.
[14] He H B, Garcia E A. Learning from imbalanced data[J]. IEEE Transactions on Knowledge and Data Engineering, 2009,21(9):1263-1284.
[15] Sun Y M, Wong A K C, Kamel M S. Classification of imbalanced data: A review [J]. International Journal of Pattern Recognition and Artificial Intelligence, 2009,23(4):687-719.
[16] Wang B X, Japkowicz N. Imbalanced data set learning with synthetic samples [C]∥IRIS Machine Learning Workshop. Ottawa, Canada: [s.n.], 2004:153-162.
[17] Batista G, Prati R, Monard M. A study of the behavior of several methods for balancing machine learning training data[J]. ACM SIGKDD Explorations Newsletter, 2004,6(1):20-29.
[18] Liu X Y, Wu J, Zhou Z H. Exploratory under sampling for class imbalance learning[C]∥Proceedings of the 2006 International Conference on Data Mining. Las Vegas, Nevada, USA: [s.n.], 2006:965-969.
[19] Quinlan J R. Improved estimates for the accuracy of small disjuncts [J]. Machine Learning, 1991, 6:93-98.
[20] Lin Y, Lee Y, Wahba G. Support vector machines for classification in nonstandard situations [J]. Machine Learning, 2002, 46:191-202.
[21] Zhou Z H, Liu X Y. Training cost-sensitive neural networks with methods addressing the class imbalance problem[J]. IEEE Transactions on Knowledge and Data Engineering, 2006,18(1):63-77.
[22] Batuwita R, Palade V. FSVM-CIL: Fuzzy support vector machines for class imbalance learning[J]. IEEE Transactions on Fuzzy Systems, 2010,18(3):558-571.
[23] Ting K M. An instance-weighting method to induce cost-sensitive trees[J]. IEEE Transactions on Knowledge and Data Engineering, 2002,14(3):659-665.
[24] Fan W, Stolfo S J, Zhang J, et al. Adacost: Misclassification cost-sensitive boosting[C]∥the 6th Int Conf Mach Learning. San Francisco, CA:[s.n.], 1999: 97-105.
[25] Sun Y, Kamel M S, Wong A AK, et al. Cost-sensitive boosting for classification of imbalanced data [J]. Pattern Recognition, 2007,40(12):3358-3378.
[26] Ting K M. A comparative study of cost-sensitive boosting algorithms[C]∥Proc 17th Int Conf Mach Learning. Stanford, CA: [s.n.], 2000:983-990.
[27] Chawla N V, Lazarevic A, Hall L O, et al. SMOTEBoost: Improving prediction of the minority class in boosting[C]∥Proceedings of the 2003 European Conference on Principles and Practice of Knowledge Discovery in Databases. Cavtat Dubrovnik, Croatia: [s.n.], 2003:107-119.
[28] Seiffert C, Khoshgoftaar T, Hulse J V, et al. Rusboost: A hybrid approach to alleviating class imbalance [J]. IEEE Transactions on Systems, Man and Cybernetics, Part A: Systems and Humans, 2010,40(1):185-197.
[29] Wang S, Yao X. Diversity analysis on imbalanced data sets by using ensemble models[C]∥IEEE Symp Comput Intell Data Mining. Nashville, Tennessee: IEEE, 2009:324-331.
[30] Barandela R, Valdovinos R M, Sanchez J S. New applications of ensembles of classifiers[J]. Pattern Analysis & Applications, 2003,6:245-256.
[31] Liu X Y, Wu J, Zhou Z H. Exploratory undersampling for classimbalance learning[J]. IEEE Transactions on Systems, Man, and Cybernetics, Part B: Cybernetics, 2009,39(2):539-550.
[32] Dean J, Ghemawat S. MapReduce: Simplified data processing on large clusters[J]. Communications of the ACM, 2008,51(1):107-113.
[33] Huang G B, Zhu Q Y, Siew C K. Extreme learning machine: Theory and applications[J]. Neurocomputing, 2006, 70(1-3):489-501.
[34] Huang G B, Chen L, Siew C K. Universal approximation using incremental constructive feedforward networks with random hidden nodes[J]. IEEE Transactions on Neural Networks, 2006,17(4):879-892.
[35] Chawla N V, Bowyer K W, Hall L O, et al. SMOTE: Synthetic minority over-sampling technique [J]. Journal Artificial Intelligence Research, 2002, 16:321-357.

