以传统文化浸润数学课堂

韩东

【摘 要】圆是小学数学“空间与图形”的最后一个平面图形，也是唯一的曲线图形。我国古代关于圆的阐述很多，文章以“圆出于方，方出于矩”“不以规矩，不能成方圆”“圆，一中同长也”三句古语为切入口，挖掘显性知识及隐性素材，引导学生通过数学的实例与思考和文化建立联系，并在文化中反思数学，在文化熏陶中学习数学，为传统文化浸润数学课堂教学提供了一个很好的思考路径。

【关键词】传统文化;圆的认识;数学教学

一、教材教法分析

圆是小学数学“空间与图形”的最后一个平面图形，也是唯一的曲线图形。《义务教育教科书教师教学用书（数学六年级上册）》指出：“从研究直线图形到研究曲线图形，对学生而言是一种跨越。因为研究曲线图形的思想、方法与直线图形相比，是有变化和提升的。因此，通过对圆的研究，学生不仅需要掌握圆的一些基础知识，还需要通过学习，感受‘化曲为直’‘等积变形’‘极限’等数学思想方法，进一步发展数学思维能力和问题解决能力。”[1]

有关圆的研究，自古以来就有记载。比如我国最古老的数学著作《周髀算经》曾记载，“圆出于方，方出于矩”;孟子在《离娄章句上》中也说，“不以规矩，不能成方圆”;墨子还为圆下了一个“定义”——圆，一中同长也。这三句古语深深地触动了笔者，并引发了些许思考。

（1）这三句古语，是否浓缩了圆的特点？教师能否以此展开本课的教学探讨？

（2）这三句古语与本课知识有什么内在联系？如何将这三句古语与本课知识进行有效组合、整合、融合、化合？

（3）这三句古语之间的内在联系是什么，是否具有包含关系、递进关系？

（4）这三句古语如何承載文化育人功能？教师如何教学才能让学生对圆的认识更深刻？

（5）传统文化印记着中华民族的文化品质和文化精神，但大多数枯涩难懂，总让学生望而生畏。如何让学生对传统文化从“望之俨然”到“即之也温”最后到“听其言也厉”的转变？

带着以上思考，秉承着将传统文化浸润到圆的教学中的原则，笔者制订了本课的教学目标。

（1）在动手操作与阅读课本中认识圆，学会用圆规画圆，探究并掌握圆的特点。

（2）挖掘传统文化的精华，探究圆的特征。

（3）在深入思考中感受极限思想的非凡魅力，在充满乐趣的数学探究活动中感受数学的趣味性。

本课教学的重难点是理解和掌握圆的特征;传统文化与圆的特征的有效融合。

二、教学过程

（一）圆出于方，方出于矩

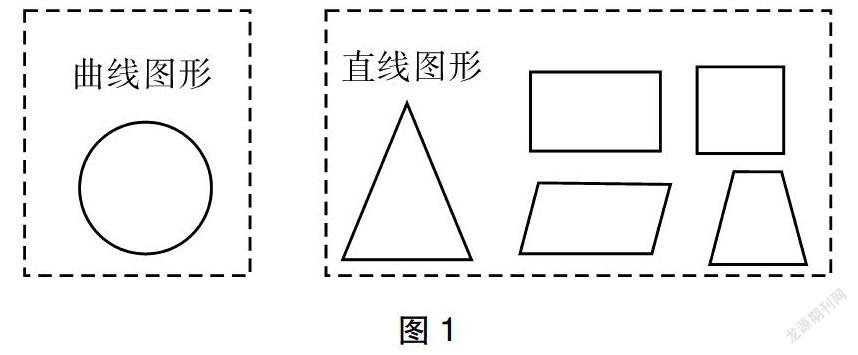
师：这里有一张正方形的纸片，如果只能用剪刀剪，你们能剪出一个标准的圆吗？

生：不能，因为圆是曲线图形，不好剪。

教师出示课件（如图1）。

师：圆是一个曲线图形，是不好剪。不过老师有办法！我们知道圆是一个轴对称图形，那么在一般情况下，轴对称图形怎样剪更好？

生：对折剪。

师（把正方形的纸片对折三次后）：直着剪一刀还是弯着剪一刀？

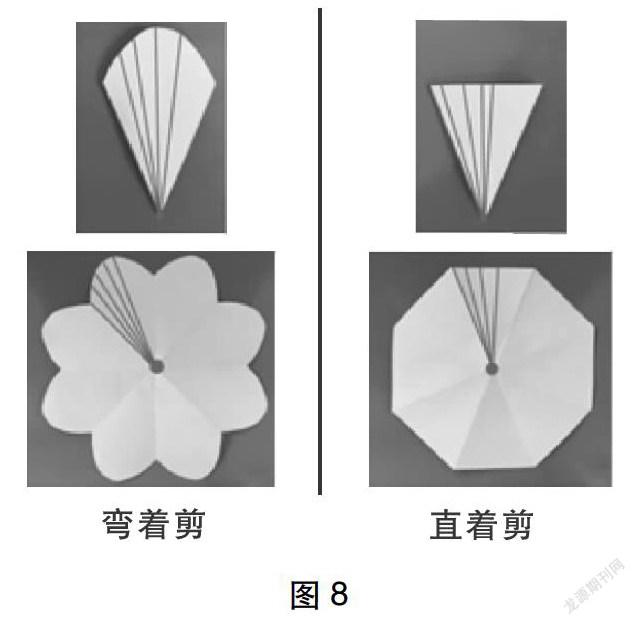
大部分学生认为，弯着剪才能得到圆，但弯着剪打开后发现，得到的并不是一个圆（如图2）。

师：怎么变成一朵花了？哪里出错了？弯着剪不能得到圆，难道要直着剪？

生（疑惑）：直着剪一刀怎么能剪出曲线图形呢？

师：我们先试试吧，看看剪出来是什么样子的。

学生直着剪一刀打开后发现，也不是一个圆（如图3）。

教师把两个图形（图2和图3）放到一起，此时学生发现：虽然直着剪也不能得到一个圆，但比刚才弯着剪更接近一个圆。

师：我们能不能将图3修剪一下，使它更像一个圆？

生：把每个棱角都剪掉。

教师用剪刀将正八边形剪成了正十六边形，果然更像一个圆了！

师：再如此剪下去会怎么样？

生：会越来越像一个圆。

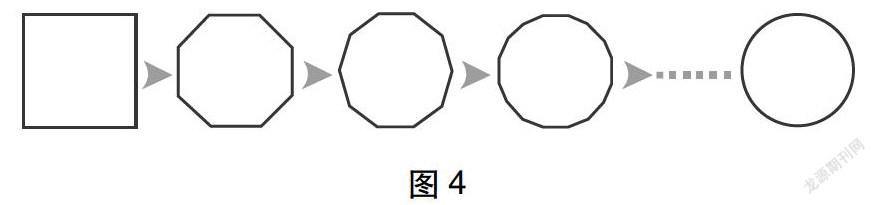
师：今天我们在课堂上无法这样继续剪下去了，但可以请电脑来帮忙。

教师用几何画板动态演示（如图4）。

师：如此切割下去，正方形纸片最终会变成什么？

生（齐声）：圆！

师：由此老师想到了一句古语——圆出于方，方出于矩。

【设计意图】爱玩是小学生的天性，特别是一些趣味性游戏，可以激发学生的学习积极性。课堂一开始就设置了一个有矛盾冲突的剪圆活动，使学生兴趣盎然，轻松快乐地进入最佳学习状态，体会“圆出于方，方出于矩”这一古语的含义。

（二）不以规矩，不能成方圆

1.画圆

（1）圆规画圆

学生尝试用圆规画圆。第一次画时，一些学生画不出标准的圆，但得出了圆规画圆的方法：定点，定长，旋转一周。按此方法，学生再次用圆规画圆。

师：用圆规画圆怎么样？

生（齐声）：很方便、快捷。

师：这又让老师想到了一句古语，“不以规矩，不成方圆”。你们知道这句古语的意思吗？

（学生说出这句话的大概意思。）

师：你们觉得这句古语有道理吗？

生（齐声）：有！

（2）圆形物品画圆

师：画圆一定要用圆规吗？

通过教师的提问，学生马上想到用圆形笔帽、透明胶带等圆形物品描出圆。

师：看来没有圆规也可以画圆，一切圆形物体描出的轮廓也是圆。

（3）操场画圆

师：老师还有个疑问，有了圆规，就一定能画出我们想要的圆吗？比如我们想要在操场上画一个大圆，怎么画？

生1：需要一个大圆规。

生2：要大圆规也没有用，谁能画得动啊！

师：看来我们就算有大圆规也很难画出一个大圆。

生3：可以在操场上插一个木桩，把绳子拴在上面，一个人拉紧绳子的另一端，绕一圈就行了。

教师出示图5，学生看后纷纷点头表示同意。

（4）引申出“不以规矩，不能成方圆”的内在含义

师：通过刚才的活动，我们知道了圆规可以画圆，但不用圆规我们也可以画圆。即使有了圆规也未必能画出我们想要的圆。那古语“不以规矩，不能成方圆”难道错了？

生3：这里的“规矩”不一定单指圆规和画直角的工具，可能是指画圆一定需要借助工具，并需要有一定的方法。

生4：“不以规矩，不能成方圆”现在引申为做人要遵循一定的章法，遵守一定的规则。

师：真了不起，你们将数学学习和哲学连在一起了。

2.自学圆各部分的名称

（1）自学课本第58页的内容。

自学提示

1.什么是圆心、半径、直径？分别用字母怎么表示？

2.在自己画出的圆中标出圆心、直径和半径。

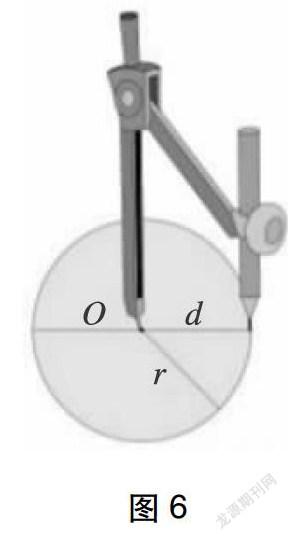
如图6，用圆规画圆时，针尖所在的点叫做圆心，一般用字母O表示。连接圆心和圆上任意一点的线段叫做半径，一般用字母r表示，半径的长度就是圆规两个脚之间的距离。通过圆心并且两端都在圆上的线段叫做直径，一般用字母d表示。

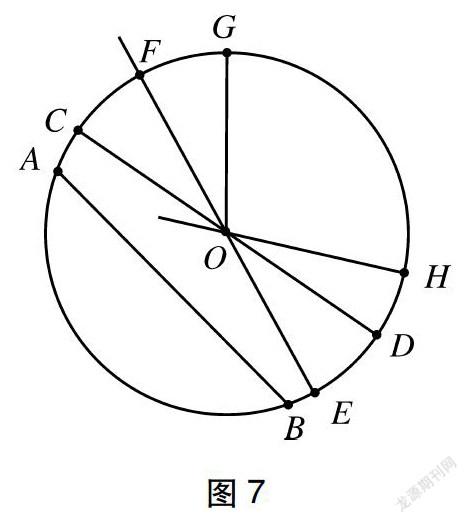
（2）判断图7中哪条线段是半径，哪条线段是直径，并说出原因。

【设计意图】“不以规矩，不能成方圆”，简单的一句古语，蕴含着深刻的哲理。本环节教师通过对这句古语的追问，让学生更深刻理解了“规矩”不仅仅是工具，还有方法、规则等方面的道理。

（三）圆，一中同长也

1.自主操作

学生沿圆的直径，折一折，画一画，量一量，看看有什么发现。

学生得出结论：（1）圆心决定圆的位置，半径决定圆的大小;（2）在同一圆中，半径和直径有无数条，且所有的半径都相等，所有的直径都相等，半径的长度是直径的一半。

2.理解“圆，一中同长也”

师：通过刚才的动手操作和交流，你们对圆的认识是不是更深入了？老师还记得在《墨子·经上》中曾记载“圆，一中同长也”。你们知道这句古语的意思吗？

学生讨论得出结论：一中即一个圆心，同长即半径都相等。

3.解释剪圆现象

师：为什么正方形纸片对折三次后弯着剪不像圆而直着剪更像圆？

生：可能是半径的问题吧？半径必须都相等才是一个圆。

教师课件演示：从中心点向边线连线（如图8）。

生：弯着剪，从中心点到边线的距离差距很大，而直着剪差距比较小，所以更像圆。

师：弯着剪一定得不到圆吗？如果可以得到，那为什么刚才弯着剪得不到圆呢？

生：弯着剪也能成一个圆，但刚才我们弯得太大了，如果弯小一点就更接近圆了。

教师按弯小一点再剪一刀，正方形纸片打开后几乎是一个圆了。

师：直着剪为什么更像圆？

生：剪的边越多，中心点到边上距离相等的线就越多。

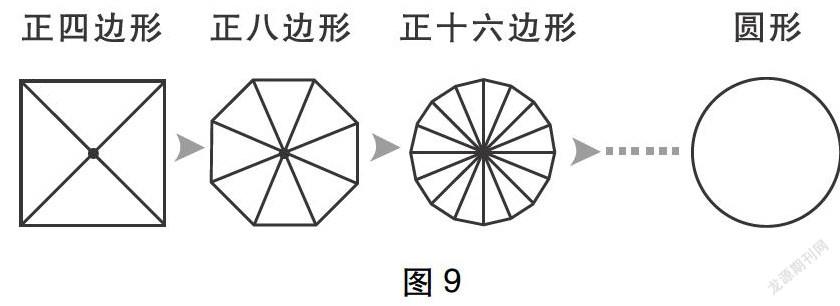
生：边数越多，同长的线就越多，就更像一个圆。

教师出示课件（如图9），得出结论：正四边形有4条同长的线，正八边形有8条，正十六边形有16条，随着边形的增加，同长的线也在增加，直到正无数边形有无数条同长的线，便形成了圆。

师：现在你们明白“圆出于方”的意思了吗？

生（齐声）：明白了。

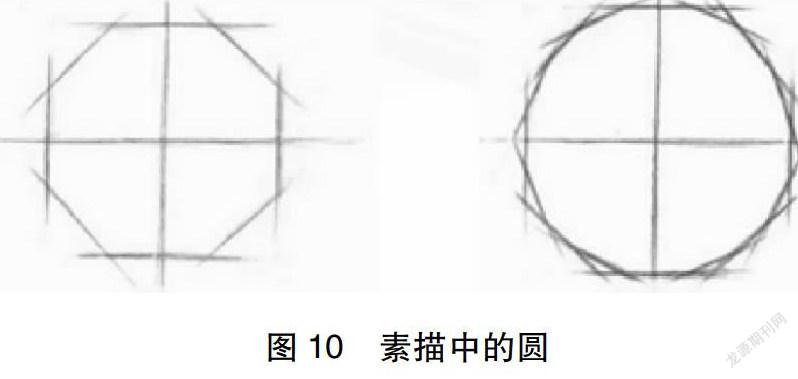
师（出示课件，如图10）：那生活中有没有这样做的？

【设计意图】本环节通过对“圆，一中同长也”进行探讨，不仅让学生理解了圆的本质特征，还轻松解决了剪圆的问题。

（四）沟通联系

师：今天在学习圆的过程中，我们认识了三句有关圆的古语。如果今天老师只想在黑板上板书其中的一句，你们认为哪句古语最合适？

学生（大多数）：圆，一中同长也。

师：为什么是这句呢？

生1：因为这句话概括出了圆的特征。

生2：“圆出于方”其实就是利用“圆一中同长”的特点，通过不断切割来保证“一中同长”。

生3：“不以规矩，不能成方圆”也是为了保证“一中同长”。

师：是的，墨子就用简单的一句话——圆，一中同长也，高度概括出圆的本质特征，这一发现比西方早一千多年。（学生由衷发出感叹声）

【设计意图】通过对三句古语的对比解读，学生把各自孤立的三句古语建立了联系，同时也感受到了中国数学文化的悠久历史和魅力，激发了爱国主义情感。

（五）生活中的圆

（1）举例说明生活中的圆。

（2）车轮为什么是圆的？车轮造成圆形就一定不颠簸吗？还要考虑什么问题？

（3）为什么有圆桌会议？

学生得出结论：圆代表着平等、尊重、团结。

【设计意图】“车轮造成圆形就一定不颠簸吗？”这一问题把圆的学习引向深入，同时又以“为什么有圆桌会议？”把圆的认识升华到哲学的高度。

三、教学反思

（一）数学的趣味性

数学是枯燥的，这是大多数学生对数学学习的感受。抽象的概念、复杂的运算和严谨的证明，使学生对数学学习望而却步。如何让学生对数学学习产生兴趣？方法有很多，而设置悬念，让学生对习以为常的事情充满疑问和好奇，是行之有效的方法之一。

“把一张正方形的紙片对折三次，要想剪出一个圆，是直着剪一刀还是弯着剪一刀？”当学生面对这个问题时，会下意识地想到“弯着剪”，因为圆是一个曲线图形。可当“弯着剪”后，正方形纸片居然变成了一朵“小花”，而“直着剪”更像一个圆，由此生发的强烈疑问驱动学生积极探究“圆的世界”。当学生明白“圆出于方”和“圆，一中同长也”后，便会深深感叹知识之间的微妙联系。

（二）文化与数学

学校作为弘扬传统文化的重要阵地，担负着创新发展、传播交流等重任，数学学科作为一门重要学科，自然也承担着这样的责任。但数学因具有理性思维的特性，很难直接表达文化与数学之间的关系。如何寻找传统文化与数学学科的结合点，培养学生的文化素養和创新思维值得教师深思。

本课以三句描述圆的古语为切入点，逐步深入地让学生认识圆，为传统文化浸润数学课堂教学提供了一个很好的思考路径。传统文化源远流长，很多内容都隐含着数学知识，有待于教师开发。但如果教师刻意地在教学中加入所谓的“文化因子”，过度地宣扬传统文化的“骄傲之处”，反而会适得其反。在本课教学中，笔者试图挖掘显性知识及隐性素材，引导学生通过数学的实例与思考和文化建立起联系，并在文化中反思数学，在文化熏陶中学习数学。

（三）极限思想

极限思想是近代数学分析问题和解决问题的一种数学思想，在数学、物理学、经济学，乃至哲学等学科中都有广泛应用，可见极限思想在学习中的重要性。但小学生因对有限事物的理解较为清晰，而对无限事物的理解较为困难的身心发展规律，如学生对推导圆的周长和面积公式的思想很难理解。极限思想在教学中的渗透，不能急于求成，教师要善于将单一、封闭、静态的形式逻辑思维提高到多维、开放、动静相结合的辩证逻辑思维，善于挖掘，并抓住时机，适度渗透。因此，在“圆的认识”一课中，笔者试图让学生通过观察有限分割，想象无限分割的终极状态，自然地在“曲”与“直”的矛盾转化中萌发无限逼近的极限思想，为后续学习圆的周长和面积公式打下基础。

（四）哲学思想

没有数学，我们无法看穿哲学的深度;而没有哲学，人们也无法看穿数学的深度;而若没有两者，人们就什么也看不透[2]。可见，数学与哲学有着密切的联系。正如柏拉图所说，数学就是理性哲学的前提条件，在哲学家的思想深处，他们的理念往往是通过数学的圆满来实现的，比如在哲学思辨中大名鼎鼎的反证法，就是一个源自数学创造的关键工具[3]。

在本课教学中，恰能很好地反映了数学中的哲学思想。首先，“不以规矩，不能成方圆”，体现了工具和章法的重要性;其次，“没有规矩就不能成方圆吗？”，体现了异曲同工的妙处;再次，“有了规矩就一定能成方圆吗？”，体现了通权达变的思想方法。这三个问题不仅有着知识层面的思考，更有着比数学知识体系更为丰富和深邃的哲学内涵。本节课的最后关于由圆到圆桌会议的探讨，也彰显了平等交流、深度汇谈的哲学意蕴。

参考文献：

[1]人民教育出版社课程教材研究所小学数学课程教材研究开发中心.义务教育教科书教师教学用书（数学六年级上册）[M].北京：人民教育出版社，2014.

[2]汪树林.数学教育：在哲学思想牵引下自由呼吸[J].中小学教师培训，2014（5）：38-41.

[3]黄逸文.从志同道合到分道扬镳：数学与哲学之间的恩怨情仇[EB/OL].（2018-03-19）.http：//www.360doc.com/content/18/0319/10/4450299_738347355.shtml.