HPM视角下的棱柱概念教学

杜金金

【摘 要】棱柱的概念是沪教版高中数学高三上册第15章第1节“多面体的概念”第一课时的内容，重在培养学生的数学抽象、几何直观等核心素养，并为后续其他几何体的学习做铺垫。教师可以从HPM视角设計本节课教学，直接或间接利用历史素材，设计一系列操作和问题，让学生在实际操作和解决问题的过程中经历棱柱定义的发生和发展过程，加深对棱柱概念的理解，发展学生相关数学核心素养以及实施数学学科德育。

【关键词】棱柱概念;核心素养;HPM视角

一、引言

棱柱是基本的立体图形。《普通高中数学课程标准（2017版）》提出，利用实物、计算机软件等观察空间图形，认识柱、锥、台、球及简单组合体的结构特征，能运用这些特征描述现实生活中简单物体的结构;在教学中，需要帮助学生逐步形成空间观念，认识空间几何体的结构特征[1]。棱柱的概念是沪教版高中数学高三上册第15章第1节“多面体的概念”第一课时的内容，沪教版教材先在第14章中引入立体几何的公理体系，系统介绍空间中的直线与平面，再在第15章中研究简单几何体。棱柱是最典型也是最常见的柱类几何体，其概念的学习重在培养学生的数学抽象、几何直观等核心素养，并为后续其他几何体的学习做铺垫。在空间几何体的学习中，学生往往存在概念理解不透、空间想象能力欠缺、考虑不全面等问题[2-3]。

在实际教学中，有些教师通过分类辨析，引导学生学习多面体与旋转体的相关概念，鼓励学生自主探究棱柱等几何体的结构特征与概念[4]。也有些教师从生活中抽象出柱体，类比线动成面，得到棱柱概念的动态定义[5-7]。实际上，棱柱的概念有着漫长的发展过程，其定义的历史演变反映了人们对棱柱概念由直观到严谨的认识过程[8]。教学实践表明，如今学生对棱柱定义的理解具有历史相似性[9]。基于棱柱概念形成的历史以及学生认知的历史相似性，有些教师设计了棱柱概念的学习单和课堂教学，重点通过探究引导学生辨析定义的严谨性，在与数学对话的过程中提升学生数学学习的自信心[10-11]。因此，将数学史融入棱柱概念有助于加深学生对棱柱概念的理解，发展相关数学核心素养以及实施数学学科德育[12]。

鉴于此，笔者从HPM的视角设计本节课的教学，并拟定如下教学目标。

（1）建构棱柱的概念，了解平行六面体、直棱柱、正棱柱的特性，能够熟练地运用定义判断各种棱柱;

（2）学会用三维空间中的基本量“点、线、面”的数量关系和位置关系研究多面体，总结其中的共性与差异，培养学生的数学抽象、几何直观等核心素养;

（3）从数学史中了解棱柱定义发展的来龙去脉，体会数学的严谨性和发展性，鼓励敢于质疑和勇于探索真理的精神。

二、历史材料及应用

1.欧氏定义

公元前3世纪，数学家欧几里得（Euclid）在《几何原本》中首次给出棱柱的定义：“一个棱柱是一个立体图形，它是由一些平面构成的，其中有两个面是相对的、相等的、相似的且平行的，其他各面都是平行四边形。”[13]这个错误的定义由于欧几里得的权威性和《几何原本》的专业性而流传了20多个世纪，一直被人们信奉和使用。

2.改进的欧氏定义

在欧氏定义的基础上，数学家通过增加侧面的属性，从而使棱柱的定义更加严谨。所增加的属性有两类。

一类为增加侧面是平行四边形且有一组对边为两个底面的对应边，如在1876年，美国数学家舒伊勒（A.Schuyler）较早给出这类定义：“棱柱是一个多面体，它有两个面为全等、平行的多边形且对应边平行，其余各面均为以全等多边形对应边为底的平行四边形。”[14]美国数学家斯顿（J.C.Stone）等人在其《立体几何》中首次给出了欧氏定义的反例[15]。

另一类为增加侧面的交线平行这一属性，美国数学家郝克斯（H.E.Hawkes）等人在其《立体几何》中给出了和现行高中数学教材中几乎一致的定义：“棱柱是一个多面体，有两个面位于两个平行平面上，其余各边均为平行四边形，且其交线平行。”[16]

3.动态定义

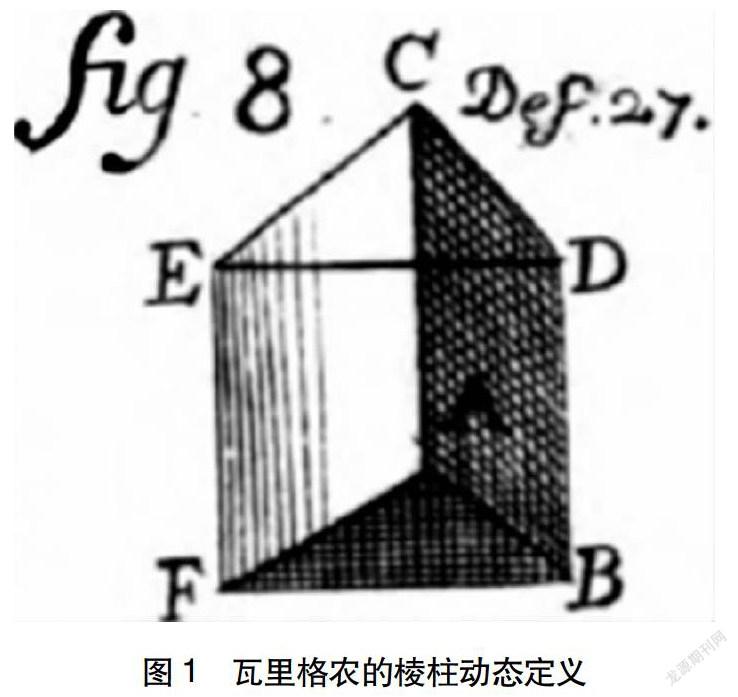
18世纪，法国数学家瓦里格农（P.Varignon）在其《数学基础》中摒弃了欧几里得的定义而采用新的动态定义：“若平面直线形（如ABF）按照平行于自身的方向从点A移动到点C，则该直线形画出一个介于两个相似且全等的图形ECD和ABF以及所有以图形ABF的边为一边的平行四边形之间的立体CB。则该立体称为棱柱。”如图1所示[8]。

三、教学设计与实施

1.小试牛刀，引出新知

课前，教师先让学生利用磁力片搭建一个封闭体。

师：同学们搭建的封闭体都很有创意，有摩天轮、变形金刚……请同学们互相观察搭建的封闭体，它们有哪些共同的特征？

生（齐答）：每个面都是多边形。

师：对，这样的几何体在生活中其实很常见。在数学中，我们把由上述平面多边形（或三角形）围成的封闭体叫做多面体，构成多面体的各平面多边形（或三角形）叫做多面体的面，其相邻多边形（或三角形）的公共边叫做多面体的棱，棱与棱的交点叫做多面体的顶点。

2.几何直观，数学抽象

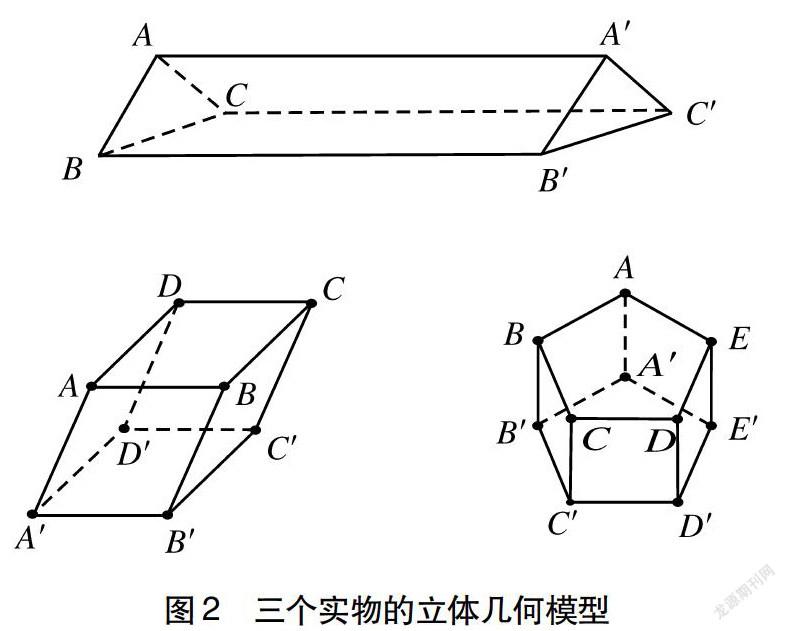
师：生活中有一类特殊的多面体也很常见，比如巧克力、斜堆的扑克牌、沙发等，因为这类多面体的构造美观且独特，才使这些商品夺人眼球，销量大增。今天我们就来研究这样一类多面体。请同学们用手中的磁力片搭建出这三个实物的模型，然后绘制出其图像（如图2）。

师：我们已经学习了立体几何，那可以从哪些角度研究多面体呢？

生1：从基本量“点、线、面”出发进行研究。

师：可以研究哪些关系呢？

生2：数量关系和位置关系。

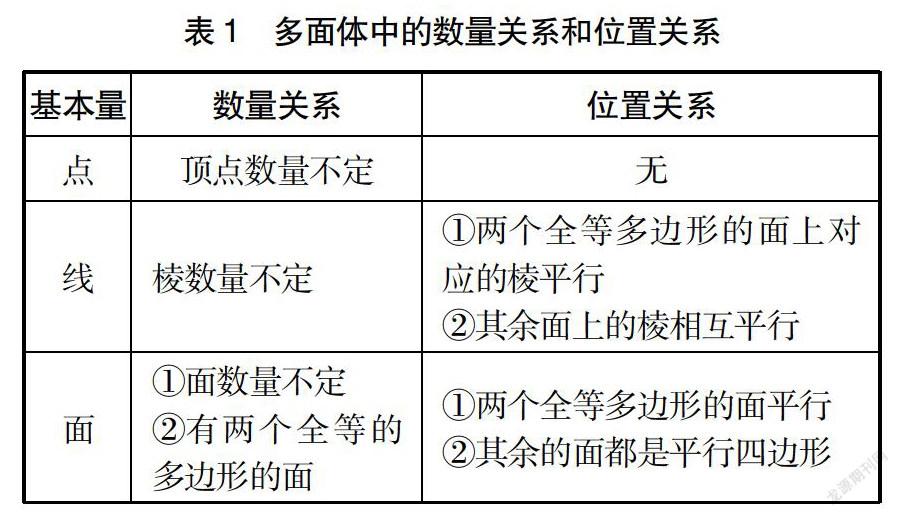
师：请同学们对照这几个多面体试着完成表1。

师：同学们的表格填写得十分正确，请同学们试着依据表1的共性对这几个从实物中抽象出的多面体下一个定义。

生3：有两个全等的多边形的面相互平行，其余各面都是平行四边形的多面体。

生4：有两个多边形的面全等且相互平行，侧面上的棱相互平行的多面体。

师：对于这样一类特殊的几何体，能否给它起一个名字。这样的几何体是什么形状？

生（齐答）：柱状。

师：柱是建筑物中的主结构件，承托在其上方物件的重量。而这样的多面体确实能作为承重结构，用柱表示非常合适。同学们在初中学过的正方体就是柱体，如果将这些多面体归类，你们认为正方体和这三个柱体是否为一类呢？

生5：斜堆的扑克牌是一种抽象的柱，它和正方体属于一类，因为两个全等且平行的多边形都是四边形，看起来结构相同。

师：我们可以通过两个全等多边形的边数进行分类，称n边形所对应的柱状多面体为“n棱柱”，统称为“棱柱”。

3.动手实践，探索真理

师：第一个给出棱柱明确定义的是数学家欧几里得，他在《几何原本》中写道：“一个棱柱是一个立体图形，它是由一些平面构成的，其中有两个面是相对的、相等的、相似的且平行的，其他各面都是平行四边形。”

生6：生3的定义和欧几里得的定义几乎一样。

师：对，非常棒！按照我们之前总结的棱柱的性质，欧几里得采用的是和“面”有关的两个性质以及和“线”有关的一个性质定义棱柱，那么能否保证剩下的一个和“线”有关的性质，即“其余的面上的棱相互平行”也正确呢？在1916年，数学家斯顿不顾众人议论，坚持说欧几里得的定义错了。同学们，你们能否用手中的磁力片为欧几里得正名，又或者为斯顿翻身呢？

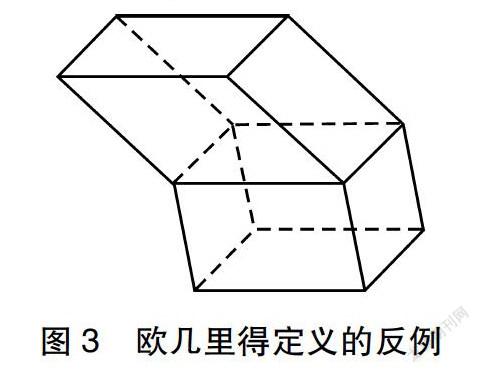
生7：斯顿说的是对的，只需要将两个四棱柱拼接即可（如图3）。

师：这的确是一个反例，也是历史上真实被举出的反例。你能不能告诉大家，如何想到构造这个反例的呢？

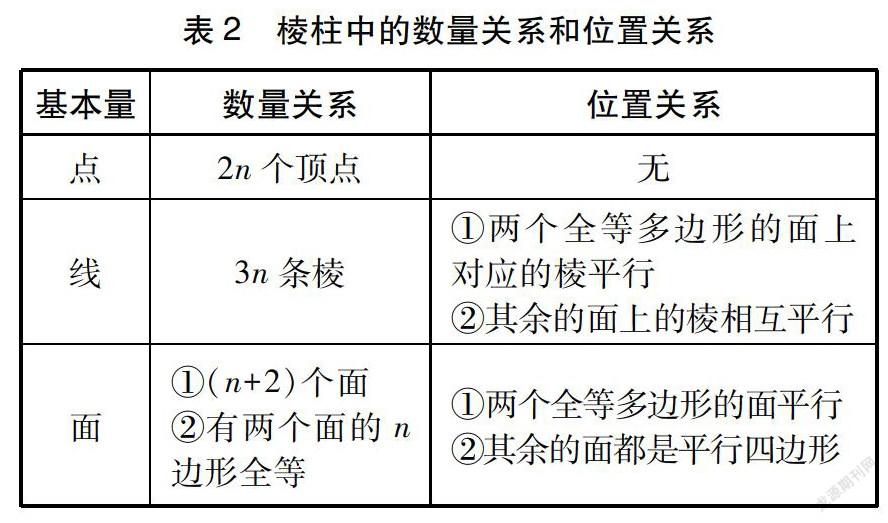
生7：我注意到了数量关系，欧几里得的定义中只限定了除两个全等多边形的面以外的面的位置关系，却没有限定数量关系。事实上n（n≥3，n∈N*）棱柱应该有2n个顶点、3n条棱和（n+2）个面。显然，四棱柱应该只有6个面，而这个多面体有11个面，因此是一个反例（见表2）。

师：但是老师作为欧几里得的支持者，认为这个反例无法说服欧几里得，也无法服众。这个反例的几何体并不常见，且局部是凹进去的，俗称凹多面体。能否再举出一个平时我们常见的多面体——凸多面体的反例，令众人不得不信服呢？

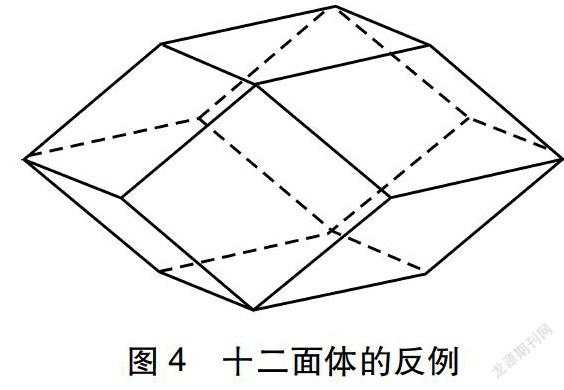
生8：可以构造一个常见的十二面体（如图4）。

师：这个反例便是斯顿当时举出的反例，它是一个凸多面体，比之前的凹多面体更常见，也与之前的反例有着异曲同工之妙。由于欧式定义无法限制面的数量，因此可以通过扩充面的数量来制造很多反例。

师：早在1876年，数学家舒伊勒就改进了欧几里得的定义：“棱柱是一个多面体，它有两个面为全等、平行的多边形且对应边平行，其余各面均为以全等多边形对应边为底的平行四边形。”你们认为舒伊勒的定义正确吗？

生（齐答）：正确。

师：紧接其后，数学家斯顿在1916年给出了十二面体的反例，给出了和舒伊勒一致的定义。1922年，数学家郝克斯和贝克等人也修改了定义：“棱柱是一个多面体，有两个面位于两个平行平面上，其余各面均为平行四边形，且其交线平行。”这也是生4的定义，请同学们判断一下这个定义是否正确，和舒伊勒、斯顿的定义相比，你们更喜欢哪一个呢？

生（齐答）：这个定义是正确的。我们觉得数学家郝克斯和贝克的定义更好一些，它不仅简洁明了，而且能体现出柱状的结构。

师：一般地，如果一个多面体有两个全等的多边形的面相互平行，且不在这两个面上的棱都相互平行，那么这个多面体叫做棱柱。棱柱的两个相互平行的面叫做棱柱的底面，其他的面叫做棱柱的侧面，棱柱的侧面都是平行四边形。不在底面上的棱叫做棱柱的側棱，两个底面间的距离叫做棱柱的高。

4.百花齐放，百家争鸣

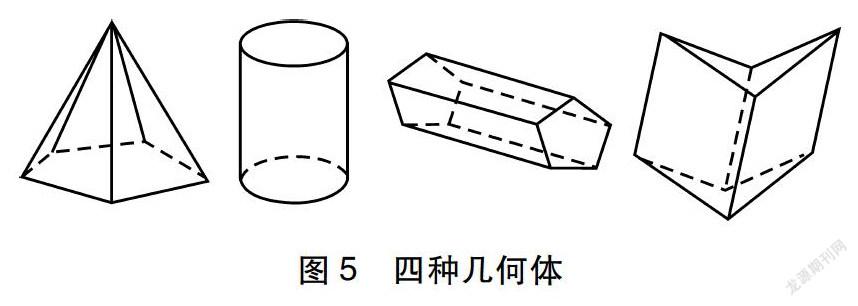
师：判断图中（如图5）的四种几何体是否为棱柱？

生（一部分齐答）：不是。

生（一部分齐答）：是。

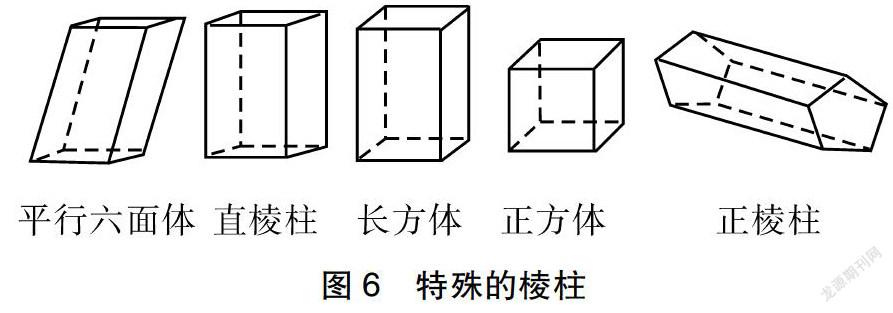
师：生活中有一些特殊的棱柱为我们所常见，请同学们依次说出它们（如图6）的典型特征或定义。

生1：平行六面体是底面为平行四边形的棱柱。

生2：直棱柱是侧棱与底面垂直的棱柱。

生3：长方体是底面为矩形的直棱柱。

生4：正方体是所有棱长都相等的长方体。

生5：正棱柱是底面为正多边形的直棱柱。

师：棱柱的发展到这里并没有停止，越来越多棱柱的应用被开发出来，百花齐放下的“蜂巢”就是典例之一。越来越多的数学家也对棱柱下了新的定义，呈现百家争鸣之势。下面请同学们观赏一个微视频，试试看能否对棱柱下一个新的定义。

生6：可以从动态的角度定义棱柱。由一个平面多边形沿某一方向平移形成的空间几何体叫做棱柱。

师：非常棒！棱柱的概念经历了从实物到定义，从崇拜到质疑，从错误到正确，从个性到共性，从复杂到简单，从单一到多样，从独树一帜到百家争鸣的过程。数学的发展也许曲折，道路荆棘，但探索真理的脚步在一代又一代人的努力下从未停止过，就像那直棱柱一般坚忍不拔！

四、学生反馈

课后，笔者收集了28名学生对本节课的反馈信息。有一半以上的学生认为，自己在课堂中给棱柱下的定义与欧几里得的一致或基本一致。

有关这节课印象最深的部分。学生提到的有：

·动手拼磁力片的过程，让我对棱柱有了清晰的概念。

·我们自己举出的那一个十二面体反例，让人震惊，也为我们自己感到骄傲。

·老师不断地让我们提出棱柱的定义，并讨论、改进，这样的试错体现了数学的魅力。

·拼搭棱柱的过程，让我意识到有时仿佛符合认知的事物其定义也不是那么显然，需要通过仔细、严谨的思考来找到结果。

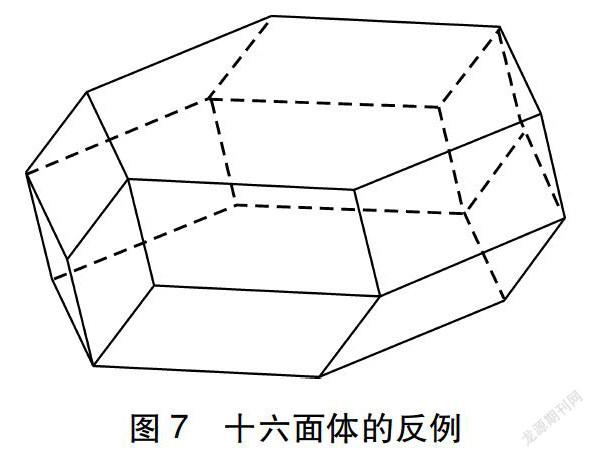
学生对课堂中的反例印象深刻，课后他们甚至自主研究出十六面体的反例（如图7）。

有关课堂中提到的“历史上的数学家也会犯错误”的事实，学生的感想有：

·后人的结论是站在前人的肩膀上得出的，所以我们通过学习，或许将来也可以再次对现在的理论进行补充或反驳。

·人无完人，谁都会犯错，即使是数学家，也会有犯错的时候，只能说理论在发展的时候总会经历错误。

·我们不能盲目相信别人，要有自己的思考，与别人不一致的时候不能盲目从众，要坚持自我，有时候少数人坚持的往往是最终的真相。

五、结语

本节课数学史的应用方式有重构式、附加式和顺应式。基于棱柱定义在数学史上的演变与发展，本节课重构了这一过程。首先，通过磁力片搭建让学生对多面体产生感性的认知。其次，通过几何体的抽象让学生关注到几何体中的点、线、面之间的关系，从而为后面棱柱定义的学习做铺垫。然后，让学生自己给棱柱下一个定义，并通过凹多面体和凸多面体各举一个反例对定义进行辨析，增强学生对棱柱的理解。最后，补充棱柱的动态定义，拓展学生的思维。其中，将学生的定义与历史上数学家的定义相比较，属于附加式;让学生辨析历史上数学家给出的棱柱定义，属于顺应式。

本节课中，从棱柱的几何特征中不断总结共性，最终得到正确的定义则是对概念的外延抽象化、严谨化和精简化的过程。学生在课堂的进程中不知不觉地经历了棱柱概念的产生过程，构建了知识之谐。课堂中磁力片的使用，很大程度上增加了学生的体验感;让学生自己给棱柱下定义，增强了学生的参与感，营造了探究之乐。在教学中，给予学生具体的实物进行全方位的观察，从中抽象出棱柱的几何模型，同时关注数量关系和位置关系，培养了学生的数学抽象和直观想象素养，实现了能力之助。

本节课中，德育之效的体现尤为明显。数学家欧几里得的错误拉近了学生与数学、与数学家之间的距离，让学生在学习知识的过程中富有情感，热情高涨。数学家的错误对于学生而言是一种警示，即不要盲目迷信权威，要敢于质疑，勇于探索真理，追求理性精神。通过对棱柱定义的不断修正，学生体会到数学是发展的，培养动态的数学观。学生并没有因为数学家欧几里得的错误而否认他在几何学中做出的巨大贡献，反而怀有包容的态度面对错误。通过修正欧几里得的错误，动手构造反例并总结出正确定义的过程，学生收获了别样的自信心和成就感。

参考文献：

[1]中华人民共和国教育部.普通高中数学课程标准[S].北京：人民教育出版社，2017.

[2]朱丹.躺下的棱柱还是柱吗？——浅谈立体几何的教学现状及由此产生的几点思考[J].数学通讯，2014（24）：9-13.

[3]傅海伦，李慧娟，柏宗玲.优化空间几何体概念教学例析[J].高中数学教与学，2017（9）：3-5.

[4]张磊.在分类中辨析数学概念：以“空间几何体的结构”的教学设计为例[J].中学教研（数学），2017（6）：14-17.

[5]张培强.课堂生成的精彩：感触“棱柱、棱锥、棱台”教学[J].中小学数学（高中版），2009（7）：19-20.

[6]汪留屿.基于直观想象素养下立体几何概念课的设计与反思：以“棱柱、棱锥和棱台”为例[J].中学教研（数学），2019（3）：21-24.

[7]刘洪璐.“棱柱、棱锥和棱台”的教学设计[J].中学数学月刊，2005（12）：4-6.

[8]洪燕君，汪晓勤.美国百年几何教科书中的棱柱定义[J].数学教育学报，2016（5）：67-72.

[9]沈金兴.中学生对棱柱的理解：历史相似性探究[J].数学通讯，2016（20）：10-14.

[10]陈锋.基于历史相似性的棱柱定义教学[J].教育研究与评论（中学教育教学），2015（5）：52-57.

[11]沈金兴.数学史视角下的棱柱定义“学习单”设计[J].数学教学，2016（11）：45-48.

[12]WANG X Q，QI C Y，WANG K.A categorization model for educational values of the history of mathematics[J].Science & Education，2017（11）：1029-1052.

[13]歐几里得.几何原本[M].西安：陕西科学技术出版社，2003.

[14]SCHUYLER A.Elements of geometry[M].Cincinnati：Wilson，Hinkle & Company，1876.

[15]STONE J C，MILLIS J F.Solid geometry[M].Chicago：B.H.Sanborn & Company，1916.

[16]HAWKES H E，LUBY W A，TOUTON F C.Solid geometry[M].Boston：Ginn & Company，1922.