“看见”内在联系 体悟数学思想

唐剑岚 王君畬

【摘 要】“圆的面积”是小学六年级上册的重点内容，其公式的推导一直是教与学的重难点，也是培育学生数学推理的良好素材。传统教学主要采用剪纸拼接的方式实现化圆为方，进而推导出圆的面积公式。这是一种“掐头去尾烧中断”的教学方式，比较生硬，且难以突显知识的内在联系和知识的发生发展过程，也难以渗透数学思想，容易导致学生满足于“知其然而不知其所以然”。文章试图将Hawgent皓骏动态数学技术深度融入其中，让学生“看见”知识的内在联系，体悟数学思想的魅力，提高推理素养。

【关键词】圆的面积;Hawgent皓骏动态数学;数学思想;创课

一、创课背景与问题

北师大版数学六年级上册“圆的面积”是小学阶段重要的学习内容，也是培育学生数学推理素养的良好素材，其中圆面积公式的推导是教与学的重难点。传统教学主要采用剪纸拼接的方式实现化圆为方，以推导出圆的面积公式。这是一种“掐头去尾烧中断”的教学方式，比较生硬，且难以凸显知识的内在联系和知识的发生发展过程，也难以渗透数学思想，容易导致学生满足于“知其然而不知其所以然”。

在学习本节内容之前，学生已经历了应用转化思想、剪切拼接等方式探讨平行四边形、三角形、梯形等由直线围成的图形面积。圆是由曲线围成的图形，从图形的外在特点来看，与其他图形的联系不大，故其面积公式的推导既是重点又是难点。如何在突出重点和破解难点的同时，提升学生的数学推理素养？本文将Hawgent皓骏动态数学技术深度融入其中，让学生“看见”知识的内在联系，体悟数学思想的魅力，提高数学推理素养，提升教学有效性，为优化圆面积的教学提供一些参考。

二、创课设计与实录

《义务教育数学课程标准（2011年版）》指出，数学知识的教学应注重学生对所学知识的理解，体会数学知识之间的关联。数学思想蕴涵在数学知识形成、发展和应用的过程中，学生在积极参与教学活动的过程中，通过独立思考、合作交流，逐步感悟数学思想，积累活动经验，提高数学素养[1]。基于课程标准理念和现实诉求，本次创课主要包括三个环节。环节一，设计“化圆形为长方形”活动，引导学生探寻圆与长方形等图形的内在联系，突显转化思想与方法的价值;引导学生基于平板电脑进行自主探究和合作交流，通过动手操作Hawgent皓骏动态数学积件，体验化圆为方的三部曲——先分割（均分成“小三角形”）后拼接再求和，加强“方”“圆”知识的内在联系。环节二，设计“化圆形为三角形”活动，再次引导学生自主学习和合作学习，应用Hawgent皓骏动态数学积件实现转化的三部曲——先分割（无数圆周长的累积）后拼接再求和。环节三，设计“化圆形为其他图形”的活动，引导学生体悟极限和转化思想，类比前两种推导方法，将圆形近似转化成三角形和梯形，进一步体悟转化思想的魅力，感受合情推理的价值[2]。根据上述创课设计思路，研究者进行了以下创课。

师：同学们，今天我们一起来探索圆的面积公式所隐藏的秘密。我们知道圆是由曲线围成的图形，从表面上看，与直线围成的图形如长方形、三角形等关系不大，但其实呢，它们之间隐藏着很深的秘密。到底是什么秘密呢？

（学生感到很疑惑。）

师：我们在推导平行四边形、三角形、梯形面积公式时，采用了相同的方法。这种方法叫什么？

生1：剪拼或割补方法，把平行四边形、三角形、梯形转化成长方形。

师：我们通过剪拼方法将平行四边形、三角形、梯形转化为长方形进而求出它们的面积，这是数学转化思想的魅力。那么圆是否也能转化成我们熟悉的图形，进而推导出它的面积公式呢？

生2：可是圆与长方形、三角形看起来有很大的不同，我们该怎么转化呢？

师：其实，我们在推导圆周长公式时，也用到转化思想，具体是怎么做的呢？

生3：我们运用了滚动法和绕绳法。

师：我们用滚动法、绕绳法实现化曲为直的转化思想，那现在是否可以类比化曲为直，实现化圆为方呢？

师：再一起来回忆一下，在推导平行四边形面积时，我们是怎样转化的？

生4：沿平行四边形的高剪开得到一个三角形，再拼接到另外一边。（生4动态演示Hawgent皓骏动态）

师：可是圆里面没有高，我们该沿什么剪开？

生5：半径或直径吧。

师：很好，大家有想法了！接下来，我们开展小组合作学习，探索圆的面积公式。在合作学习中，我们要注意三点。（1）先自主探究，再相互交流，最后展示分享;（2）操作平板电脑里面的Hawgent皓骏动态数学积件，探究化圆为方的秘密，并思考这样转化的原因;（3）提出同全班分享的问题或困惑。

小圆（代表圆圆组汇报）：我们发现将圆平均分时，可以很好地拼成我们学过的图形。（小圆动手操作Hawgent皓骏动态数学积件，如图1。）首先，输入数字8将圆平均分成8等份;接着，将8份圆展开，再把它们拼接起来，得到类似于平行四边形的图形;然后，继续将圆平均分成16、32、128份等，重復前面的操作。如此细分下去，随着分成的份数越多，我们发现拼成的图形越来越像长方形。

生1：真神奇，为什么会出现这样神奇的效果呢？

师：我们不光要看到圆变为长方形的过程，还要看到变化的结果，进一步发现它们的面积公式的秘密。（教师操作Hawgent皓骏动态数学积件，展示将圆无限细分的动态过程。）当圆变为长方形时，长方形的长和宽分别是多少？

小圆：这里的长是圆周长的一半，即πr，宽是圆半径r。圆的面积等于圆周长的一半乘以圆半径，故圆的面积公式为S=πr2。

师：你们现在发现圆与长方形的神秘关系了吧！（教师再次演示将圆无限细分的动态过程，让学生再次经历化圆为方的过程，“看见”长方形的边长和圆的周长与半径的内在联系。）在这个推导过程中，我们应用了什么方法，感受到了什么思想的魅力？

生（齐）：我们感受到了割补、转化思想的魅力，Hawgent皓骏动态数学积件太厉害了。

师：我们通过无限分割和有意（强调按照我们想要的图形）拼接，将圆转化为长方形，再次体验了转化的魅力，这在大学里叫做无限分割、以曲代直、拼接求和的极限思想和微积分思想。除了这样的方法，我们可以将圆转化为三角形等图形来推导圆的面积吗？请小组继续合作探究，借助Hawgent皓骏动态数学积件，探索圆与三角形的神秘关系。

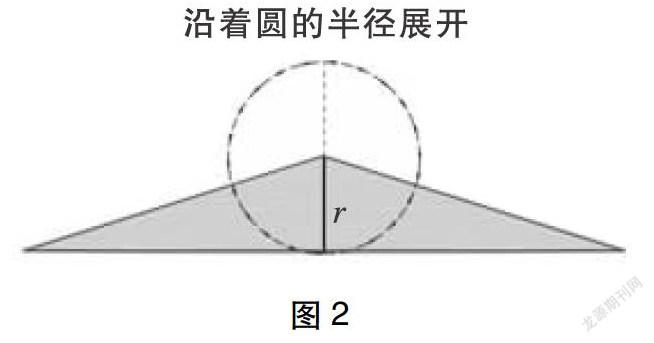
小方（代表方方组汇报）：通过操作Hawgent皓骏动态数学积件看到，整个圆面由无数个半径大小有序变化从0到r的圆拼接绕成，沿着这些圆的半径剪开，展开并有序拼接这些圆，就转化成了等腰三角形，而求圆的面积就转化成求等腰三角形的面积。我们就神奇地发现圆与三角形的关系了。（小方动手操作Hawgent皓骏动态数学积件，如图2。）

生2：的确很神奇啊！那等腰三角形的面积是多少？底和高分别是多少？

师：生2提问得很好。这个等腰三角形的底与圆的什么有关系，高又是多少呢？

小方：三角形的底就是圆的周长，即2πr，高是圆的半径r，故圆的面积公式为S=πr2。

师：小方解释得很好。（教师再次演示无限分割、以曲代直、拼接求和的动态过程，让学生“看见”三角形与圆的内在联系。）在这个推导过程中，我们应用了什么方法，感受到了什么思想的魅力？

小方：应用了推导圆周长的化曲为直的转化方法——无限分割和有意拼接，我们再次感受到了无限分割、以曲代直、拼接求和等极限思想的魅力。

师：小方总结得很好！从这两个推导的过程中，我们深刻地体悟到了无限分割、以曲代直、拼接求和等思想方法的魅力。除了上面两种转化方法，我们还可以将圆转化为更多的图形进而推导圆的面积吗？我们再次小组探究，类比前两种转化方法，将圆平均分成16份或17份，看看还能发现什么秘密？

师：这个想法很好。你们是如何想到的？

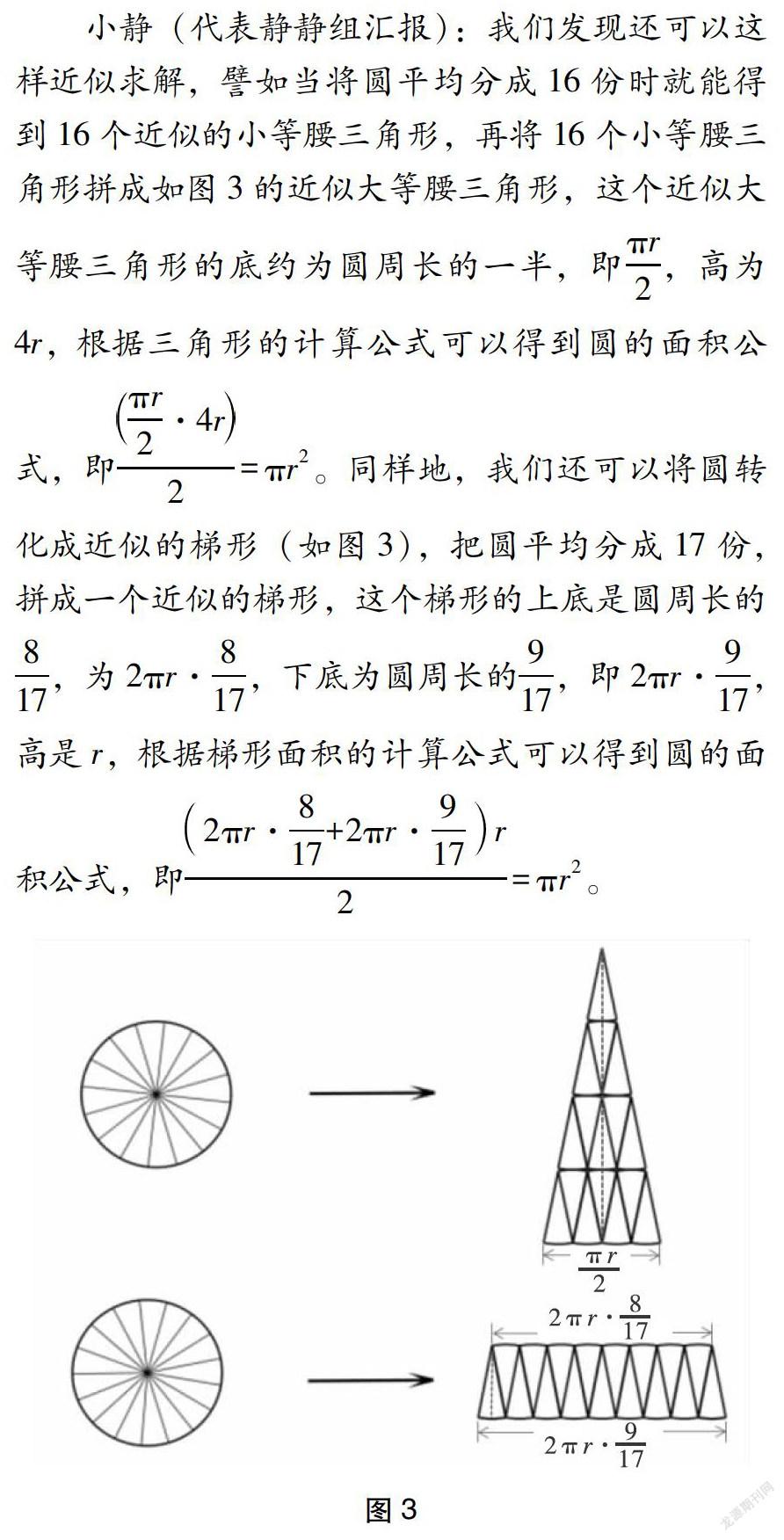
小静：类比前两种推导方法想到的，但这其实是一种近似求解的方法。

师：有道理，近似求解也是一种方法。这种方法也能够推导出圆的面积公式，主要原因还是极限思想的作用。本节课我们获得了三种推导圆面积公式的方法，感受到了转化思想的神奇魅力。其实借助今天的转化思想，推导圆的面积公式还有不需要拼接的方法，这就留给同学们课后进行思考吧！

三、创课评析与反思

技术深度融入教学，不只是技术本身有优势，更关键的是将技术与教学对象（谁来教学）、教学内容（教学什么）、教学方法（怎样教学）和教学评价（教学得如何）“五位一体”深度融合，才能形成生生不息的教学生产力[3]。针对“圆的面积公式为什么是这样，与长方形、三角形等图形的面积公式究竟有什么关系”的问题，笔者调研后发现，九成以上的教师和学生只知道圆的面积公式是S=πr2，但不知道为什么是这样子，處于一种“知其然而不知其所以然”的状态，更谈不上“知何以知其所以然”。这也是笔者做这个研究的初心。本文试图将信息技术深度融入圆的面积公式教学，努力解决“圆的面积公式为什么是这样”的问题。本次创课应该是信息技术深度融入数学教学的典范，具有两个突出的亮点。

1.“信息技术+活动单”，发挥“双主”作用

一般而言，活动单是教师设计让学生经历学习活动的清单。这种活动往往不好发挥教师的主导作用。因此，这里设计的活动单（三个具体活动：化圆为长方形、化圆为三角形、化圆为其他图形），不仅能充分发挥学生的主体作用，还能充分发挥教师的主导作用。这三个具体活动，一方面让学生有效开展合作探究，引导学生基于Hawgent皓骏动态数学积件，优化学习方式;另一方面，便于教师提问、点拨与启发，推进学生有效经历学习活动的过程，体悟活动结果。譬如，当学生能够说出三角形与圆的关系时，教师再次演示无限分割、以曲代直、拼接求和的动态过程，让学生“看见”三角形与圆的内在联系，并再次追问“这个推导过程，我们应用了什么方法，感受到了什么思想的魅力？”在信息技术的助力下，教师的点拨活动可能更有效引导学生有序经历圆面积的推导过程，促进学生有效、深刻地体悟实现数学推理背后的转化思想及其原理。

2.“信息技术+提问链”，“看见”内在联系，体悟数学思想

从理论上来说，绝大多数数学知识是具有内在联系的，只是有些是显性联系，有些是隐性联系。其中，圆与长方形、三角形等图形的内在联系是隐性的，要让学生“看见”它们的内在联系，体悟数学思想，在传统课堂上是难以做到的。这里设计的“信息技术+提问链”，可谓“双镜观察”，可助力实现授人以“鱼”的同时授人以“渔与欲”[3]。信息技术扮演“放大镜”的角色，可以帮助学生看清事物的内在联系，特别有助于学生自我反思习惯的养成。譬如在本文中，借助Hawgent皓骏动态数学积件，通过聚焦“化圆为长方形”和“化圆为三角形”的过程，视觉化圆与长方形、圆与三角形的联系。而提问链扮演“望远镜”的角色，可以帮助学生站得高、看得远、走得稳，特别有助于数学思维品质的提升。譬如，教师通过提问链“那么圆是否也能转化成我们熟悉的图形，进而推导出它的面积公式呢？”“在这个推导过程中，我们应用了什么方法，感受到了什么思想的魅力？”“这个等腰三角形的底与圆的什么有关系，高又是多少呢？”等深度追问，引导学生不仅仅看到了圆与其他图形的显性联系，而且深度体验到了化圆为方、化曲为直、近似求解的转化思想和极限思想的魅力，提升了学生的数学思维品质。

参考文献：

[1]中华人民共和国教育部.义务教育数学课程标准（2011年版）[S].北京：北京师范大学出版社，2011.

[2]毛亚峰.借助操作，深化“转化”思想：“圆的面积”教学实践与思考[J].小学教学参考，2019（5）：19-21.

[3]唐剑岚.“鱼渔欲”三位一体优化数学教学的理念与策略：以“三角形的内角”课例片段分析为例[J].基础教育研究，2015（9）：5-10.