浅谈初中数学教学中学生逆向思维能力的培养

姜强

【摘要】在人教版的初中数学教材中，从几何图形开始，在教材习题中就逐渐出现图形与方程式结合运算的例题，而在图形性质证明中，可以通过多个不同的性质理论证明。由此可见，这就需要教师在初中数学教学中，培养初中生的逆向思维能力，提高初中生的数学解题水准。因此，本文以培养初中生的逆向思维能力为主进行分析。

【关键词】初中数学教学;逆向思维;培养

在初中数学中的逆向思维，主要表现在同一类型题目可以使用多种方法求解，或将题目条件进行多次倒置，再进行求解。但是，在解题过程中，初中生会受到定式思维及传统教育观念的干扰，从而导致逆向思维能力的发展受阻。因此，本文将分析这两方面对逆向思维的影响，并提出两项改善措施。

一、影响初中生提高逆向思维能力的因素

（一）定式思维会束缚初中生的解题思维

为了响应新课改的要求，初中数学应转向以培养初中生自主学习意识为主的教学方式，让初中生通过大量的数学实践，形成举一反三的数学逆向逻辑思维，进而提高初中生的数学解题能力。而在初中数学课堂中，大多数学教师还是以教师主导作为课堂教学的主要方式，总是引导初中生跟随自己的讲解方式解题。这样虽然可以让初中生在短时间内按照固定的套路解出答案，但是久而久之，针对某一题型，初中生就会形成定式思维，一旦遇到题型变式，反而陷入解题困境。

（二）过度重视卷面成绩，追求做题速度

我国的教学模式一直是以应试教育为主，从学生入学的那一天起，就注定要经过小升初、初升高、高升大等一系列考试，所以书面成绩在学校及家长的眼里比什么都重要，因此作为受教者的学生，也自然而然地被灌输了这种思想，从而渐渐地失去了对学习本质上的热爱。而中学的校方在制订学年计划时，尤其是从初二开始，往往会在短时间内安排数次的大小考试，如周考、月考、小考、模拟考等多种类型的考试。虽然这些对于初中生而言，一方面可以巩固复习课堂学习内容，另一方面还可以促使初中生产生紧张的学习意识。但是，恰恰是这源源不断的考试卷子，使初中生变得急躁不安，而且越来越疲惫于卷面考试，从而在解题时只在乎解题速度，并不在乎解题质量，进而限制了数学逆向思维的发展。

二、提高初中生逆向思维能力的措施

（一）通过一题多解的方式培养初中生的逆向思维一般而言，在数学学科中有些数学理论的概述

过于专业化，对于初中生而言，理解起来比较抽象。因此，这就需要数学教师运用数学逆向思维，采用同一例題解出两种解法的教学方式，加深初中生对数学逆向思维的理解程度。

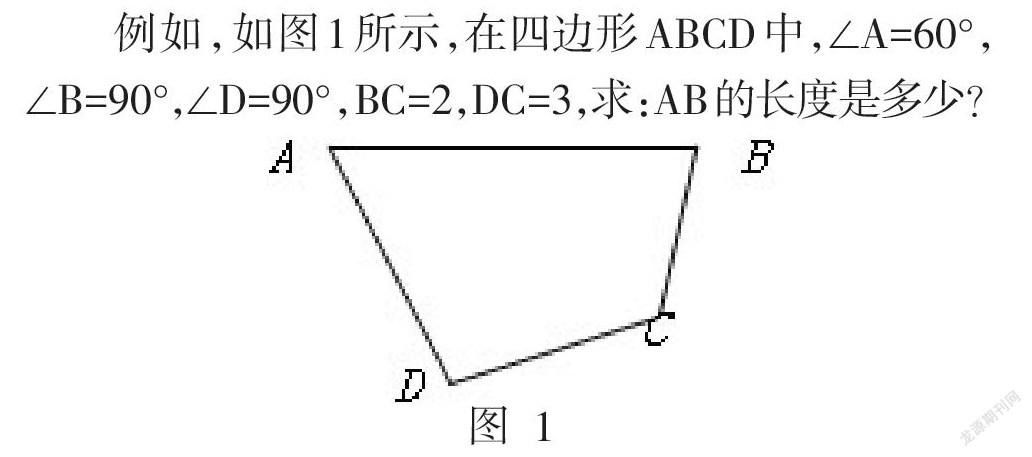
例如，如图1所示，在四边形ABCD中，∠A=60°，

∠B=90°，∠D=90°，BC=2，DC=3，求：AB的长度是多少？

方法1：解：延长AB，CD交F，

∵∠A=60°，∠D=90°（已知），

∴∠F=30°（三角形三个内角之和为180°），

∵∠B=90°，BC=2（已知），

∴CF=2BC=4（直角三角形中30°角所对的直角边是斜边的一半），

又∵CD=3，

∴DF=CD+CF=7，

而在RT△FBC中，BF2+BC2=CF2，解得BF=23，

∵在RT△F3AD中，AD2+DF2=AF2，且2AD=AF，7

∴AB=AF-BF=3143-2383。

方法2：解：延长AD，BC交E，

∵∠A=60°，∠B=90°（已知），

∴∠E=30°（三角形三个内角和为180°），

∵∠D=90°，CD=3（已知），

∴CE=2CD=6（直角三角形中30°角所对的直角边是斜边的一半），AE=2AB（同上），

又∵BC=2，

∴BE=B3C+CE=8，

因此，由该例题的多种解法可以看出，通过对同一问题的逆向思索，可以衍生出多种不同的解题方式，进而提升学生自身的数学图形解题能力。

（二）利用引导性提问培养初中生逆向思维

在以往的初中数学教学中，针对课堂例题的提问，大多数教师都是以肯定的方式提问，如：“这道题的解题方式就是这样的吗？”这种方式的语句中含有指向性的词语，如“就是”和“这样”等词语，而这就很容易将学生的解题思路约束在题目要求中，从而限制学生运用逆向思维拓展解题思路。因此，这就需要数学教师在上课提问的时候，通过一些积极的引导性提问，引发初中生对逆反思维的思考。例如，在学习“平行四边形”后可知，证明平行四边形可以从图形的边和角两方面着手思考，并且可以利用多个不同的性质理论进行证明，如“如果一个图形的每组相应的对边长度都是一致的，那么就说明这个图形一定就是平行四边形”，或者“如果一个图形的每组相应的对角度数都是一致的，那么同样说明这个图形是平行四边形”。

三、结语

通过一题多解和引导性提问这两种方式，可以培养初中生的逆向思维能力，也可以提高初中生的数学解题效率，从而促进初中生的整体数学能力发展。参考文献：

[1]宁江丽.初中数学教学中学生逆向思维能力的培养初探[J].新课程，2018（5）.

（责任编辑 林娟）