如何在解题教学中培养学生的思维发展
☉甘肃省民乐县职教中心学校 钱 沛
掌握数学即意味着解题者善于解决一些标准题以及一些要求独立思考、思路合理、有发现创造的题.揭开“条件”和“结论”之间的内在联系,并从“已知”的探索中导出“未知”的结论就是解题,解题思路正是在运用揭开手段以及探索技巧时的具体体现.数学解题活动,这一借助数学知识来分析问题、解决问题的思维活动具有明显的思维深刻性、灵活性、独创性、广阔性、敏捷性、批判性,数学思维活动的成果在数学解题方法的呈现中得到了具体的体现.
笔者认为,发展学生数学思维的教学应从如下几个方面设计与落实.
一、加强反思
学生对事物规律的认识往往能在其思维的深刻性上表现出巨大的差异.学生思维的深刻性是其有效解题的重要基础.教师在具体的解题教学中应引导学生对解题过程进行积极地反思并因此促进其思维深刻性的发展.
设u=x2-x,则
从结论上来看,这一解题过程明显不对,但学生对于错在哪里却始终摸不清头脑.此时,教师可以引导学生对其解题过程中的每一步进行推理并重新思考.学生很快发现,解题时首先应确定函数的定义域:(0,1)∪(1,2].接着根据得出,当u取最小值时y取得最大值,这是不够严密的.因为函数在其定义域∪(0,2]上并不是单调递减的,应对其进行分区间考虑才行,因此可得出函数的值域为当然,运用判别式法求值域也是可行的.学生在解题反思中也获得了思维深刻性的锻炼与发展.
二、突破思维定式
解题能力在数学学习过程中是思维的灵活性的具体表现,因此思维灵活性也是一种重要的思维品质,学生一旦具备思维的灵活性就能够在不同的解题思路中灵活转化.学生形成思维定式的一般表现就是多次运用同一思维方式对同一类问题进行解题,在解题中一般都会作出习惯性的反应,而且不作新的探讨.思维定式在学生运用同化的方式来发展其认识结构时往往能够表现出其积极作用的一面,教师在解题教学中引导学生举一反三实际上就是充分发挥思维定式的积极作用的具体操作.思维定式在学生运用异化或调整的方式来发展其认识结构时往往体现出其干扰作用的一面,教师此时应帮助学生克服思维定式的负面效应,并使其获得思维灵活性的发展.
例如,试求抛物线y=4x2的焦点坐标.
有学生在二次函数知识的影响下往往会立即得出焦点为F(0,1),这明显不对.这是在圆锥曲线的教学中出现的一题,学生的思维仍旧陷于二次函数的图像中,教师应引导学生变换条件并将方程改写为,进而迅速地得出焦点为
由此可见,教师关注题目条件的变更能帮助学生克服思维定式带来的负面影响,并令其思维灵活性得到发展.
三、打破思维常规
学生在数学学习过程中能够独立思考、分析、解决问题并具有探索与创新的精神即为其思维独创性的表现.事实上,很多学生在解题时都会受到传统解法的约束并表现出不能接受违反“常规”的解法的思想,很多学生在各类题目中仅仅满足于解题成功的快感,而在解题技巧、解法探索上不能进行深刻的探索,解题速度缓慢也是普遍存在的弱点.教师应高度关注这些现象,以此引导学生对多种解法进行思考和探索,帮助学生在多种方法尝试解题的过程中总结简捷明快的解法,这也是培养学生创造力的有效手段.如果任由学生养成照本宣科、生搬硬套的解题习惯,定会令学生获得题越做越死、思路越走越窄的学习感受,因此,教师在具体的教学过程中一定要帮助学生打破常规并使其思维的独创性得到发展.
例如,利用一般解法求sin210°+sin250°+sin10°sin50°的值时,解法如下:
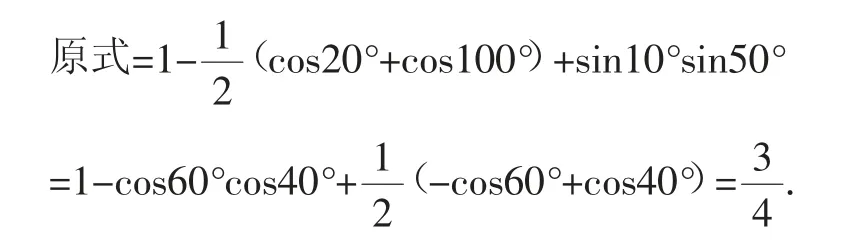
不过,教师如果能从三角函数的平方关系上引导学生进行解题的思考,就会有学生想到以下解法:

这种构造对偶式求解的思路表现出了学生独创性的解题思维.
四、优化知识结构
引导学生从各个条件联系的关节点上探索多种解题途径能够有效地培养学生思维的广阔性.因此,教师应不断引导学生对题目进行多角度、多方位的思考并促进学生知识结构的不断优化,使学生在不断加强知识点之间联系的同时获得思维广阔性的发展.
例如,已知a2+b2=1,c2+d2=1,求证:|ac+bd|≤1.
这种从平方和的相等关系出发来探索乘积和的不等关系的题目对于解题者思维广度的要求较高.大部分学生在证明此题时会运用到比较法、综合法和分析法.教师可以引导学生对式子的整体结构进行观察并令其发掘题目中的隐含条件,促进学生思维发散的同时令其获得其他的证明方法.有学生在一定的观察、分析和联想之后获得了三角函数的证明方法:
因为a2+b2=1,c2+d2=1,因此可令a=sinα,b=cosα,c=cosβ,d=sinβ.
所以|ac+bd|=|sinαcosβ+cosαsinβ|=|sin(α+β)|.
因为|sin(α+β)|≤1,所以|ac+bd|≤1.
学生的思路在这样的训练中能够得到有效的开拓,其学习兴趣也会因此变得更加浓厚.
五、强化限时训练
学生思维的敏捷性一般表现在其运算环节与推理过程的缩减上,高考对于学生全面掌握知识作出要求,对有限时间内是否能够迅速提取大脑所贮存的相关知识并加以综合运用也提出了要求.

联想正弦函数的有界性|sinθ|≤1即可使问题得到迅速地解决.
教师在具体的解题教学中应做到以下几点来培养学生思维的敏捷性:(1)帮助学生熟练掌握基础知识与技能;(2)教会学生预先思考并引导学生在教师讲授过程中获得一定的思路,使学生能够有效地提取大脑中所贮存的知识并将其运用到具体的思维活动中;(3)精心设计限时作业并使学生在层次合理的训练中提升作业效率.
六、加强错题教学
学生在解题中能够严格估计思维材料并精细检查思维过程能令其更加准确地解题,这是学生在解题过程中的一种趋向与能力,具备较强批判性思维的学生往往能够更好地发现自己的错误之处并寻得症结所在,解题的正确率也会因此得到保证.
例如如下一题:已知a、b、c均不相等,且abc=0,a2=bc,b2=ac.求证:a+b+c=0.
参考答案如下:
证明:因为a2=bc,b2=ac,所以a2-b2=bc-ac,即(a+b)·(a-b)=-c(a-b).
又a≠b,所以a+b=-c,a+b+c=0.
有学生在推敲后发现:根据题设可以得出b、c同号且a、c同号,因此a、b、c同号,所以a+b+c≠0.跟题目要求证明的关系式相互矛盾.实际上,参考答案中体现出的推理并没有错误之处,只因为原题本身是错误的.
很多学生的数学思维都缺乏一定的批判性,这是教师在具体教学中应该关注的.
当然,学生思维的发展不可能一蹴而就,教师在平日的教学中应不断加强引导并从上述各方面落实符合学生实际的具体教学,使学生的思维在有的放矢的针对性教学中获得全面发展.

