例谈几何习题的拓展

☉福建省南平市高级中学 陈 军

凝结着教育专家智慧结晶的例题或习题尤其具有典型性与代表性，教师在具体的教学中应善于通过习题、例题的拓展研究以促进学生对数学知识、方法的理解、掌握和应用.本文结合一道具有代表性的习题，通过问题条件、背景、结论的改变对习题的拓展延伸进行了思考.

作为知识主要来源的教材也是教师授课的依据，对于高考命题来说也是极为重要的载体，很多高考试题都是从教材中的例题或习题变式得来的，因此，教师在例题、习题的基础上进行拓展延伸教学也就变得极为重要了.

例1如图1，60°的二面角的棱上有A、B两点，直线AC、BD分别在该二面角的两个半平面内，且均垂直于AB，已知AB=4，AC=6，BD=8，求CD的长.

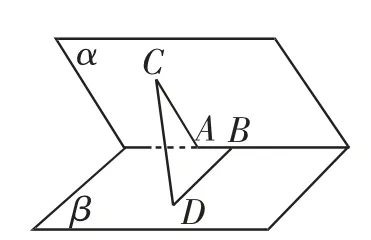
图1

解决几何问题不外乎几何法与向量法这两种最主要的途径.构造三角形并将二面角的平面角置于三角形中求解的方法即为几何法.运用向量法解题时一般有借助向量的几何运算解题和运用向量的坐标运算解题这两种方式，因此例题中的问题可有两种解法.

解法1（几何法）：如图2，在平面β内作AE⊥AB且AE=BD，连结CE、ED.因为AE⊥AB、BD⊥AB、AE=BD，因此四边形ABDE是矩形.因此ED∥AB，ED=AB=4.

因为AB⊥CA，AB⊥AE，因此AB垂直于△CEA所在的平面，即ED垂直于△CEA所在的平面.因此ED⊥EC.因此△CED是直角三角形，∠CED=90°.

在△CEA中，利用余弦定理可得CE2=CA2+AE2-2CA·AEcos60°，解得CE2=52，在△CED中，CD2=CE2+ED2，解得CD=

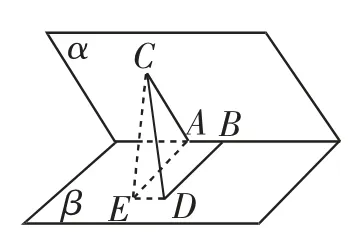
图2

解法2（向量法）：如图1，因为AC⊥AB，BD⊥AB，且二面角是60°，因此〈

以此题作为背景进行拓展研究.

一、逆向探究

例2已知A、B两点在二面角的棱上，直线AC、BD分别在该二面角的两个半平面内，且均垂直于AB.若AB=4，AC=6，BD=8，则该二面角的大小是______.

解析：如图2，由题意作辅助点E，使AE∥BD，DE∥AB，则DE⊥CE.

另外可知AE=BD=8，设二面角的大小是θ，则在△AEC中，利用余弦定理可得，所以θ=60°，即该二面角的大小是60°.故填答案：60°.

评注：将原题中的条件和结论互换并进行新题的编写，能使学生对知识的灵活应用能力得到锻炼.

二、变换背景

例3如图3所示，墙面为射击训练墙，某射击运动员在点A处进行射击训练，点A至墙面的距离为AB，某目标点P沿墙面上的射线CM移动，计算由点A观察点P的仰角θ的大小有助于更精准地击中目标.若AB=15m，AC=25m，∠BCM=30°，则tanθ的最大值为______.（直线AP和平面ABC所成角记作θ）

图3

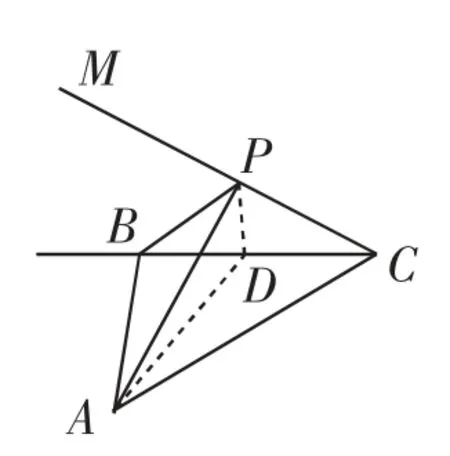
图4

解析：由勾股定理可得BC=20m.如图4所示，过点P作PD⊥BC于点D，连结AD，则由点A观察点P的仰角θ=∠PAD，且.

评注：本题的变化在于定点到动点、角的大小到最值问题的改变，引入变量并构造目标函数即可令函数的最值得解.二次函数配方法、均值不等式法、三角换元法、导数法都能用于函数最值问题的求解上.

三、改变条件

图5

例4如图5，已知平面α∩β=l，A、B为l上的两个点，C、D在平面β内，且DA⊥α，CB⊥α，AD=4，AB=6，BC=8，动点P在平面α上，令∠APD=∠BPC，则△PAB的最大面积为（ ）.

解法1：由题意可知，平面α⊥平面β，A、B为平面α和β的交线上的两个定点，DA⊂β，CB⊂β，且DA⊥α，CB⊥α，因此△PAD、△PBC为直角三角形.又∠APD=∠BPC，所以△PAD∽△PBC.又AD=4，BC=8，所以PB=2PA.作PM⊥AB，垂足为M，则PM⊥β.令AM=t∈R，则在两个Rt△PAM和Rt△PBM中，PM为公共边及PB=2PA，因此PA2-t2=4PA2-（6-t）2，解得PA2=12-4t，因此PM=

于是△PAB的高的最大值是4，故（S△PAB）max=12，因此选C.

因为∠APD=∠BPC，因此PB=2PA，以AB的中点O为坐标原点，建立直角坐标系，如图6所示.设P（x，y），A（-3，0），B（3，0），由PB=2PA，得，化简得（x+5）2+y2=16（y≠0）.

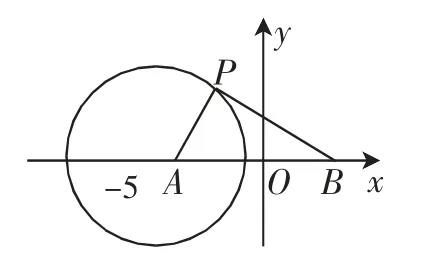
图6

因此点P的轨迹为圆心是（-5，0）、半径是4的圆，因此△PAB的高的最大值即为圆的半径（不包括x轴上的点），故（S△PAB）max=12，因此选C.

评注：解法1中所运用的几何法相对繁琐，解法2中采用的解析法则相对简洁，数、形之间的双向依存关系在几何问题代数化之后得到了很好的体现.

四、改变方法

图7

解析：作AE⊥BC于E，连结DE，则由AD⊥BC，得BC⊥平面ADE，故DE⊥BC.所以∠AED为二面角α-l-β的平面角，∠AED=θ，∠ADE为AD和面β所成的角，

评注：巧妙运用三角形的面积比和正弦定理的关系来解题的方法令人耳目一新，的获得令问题变得简单且令人感叹.

因此，教师应善于挖掘经典习题并引导学生对问题的本质展开探究，使学生能够在不变应万变的解题中获得能力的提升.