强化应用题教学,提高学生建模等数学素养
——浅议高中数学应用题的教学现状与对策
☉江苏省金湖中学 陈万斌
数学不是空洞的,也不完全是抽象的,数学来源于实践又服务于实践,而数学应用题正是培养学生运用数学知识和方法来解决实际问题的能力,体现出数学的无处不在与无所不能.数学应用题是考查学生分析问题和解决问题的能力,也是高考的重要组成部分,在每年的高考中所占分值较大,一般江苏省高考应用题处于试卷解答题的中间位置,是中等生和优等生得高分的基础,若处理不好,往往会影响后面的习题解答,进而直接影响到最终的数学成绩.但就目前学生的现状来说,一是畏惧应用题,阅读能力不高,特别是遇到题目较长、字母较多、数量关系较复杂的题目时就缺乏坚持读题的信心;二是解决应用题时缺乏耐心,读题草率,审题不仔细,特别是不善于列出有用信息,并找出关键句;三是不会建模,特别是遇到陌生的数学情境时就会茫然不知所措.这就要求我们数学教师要加强应用题教学,并对应用题进行深入的研究,进而帮助学生找到应用题的解决办法,希望本文能对教师开展应用题的复习课教学有所帮助.
一、案例分析
(一)近期考题再次分析
下面例题是江苏省淮安市高三三模试卷中的数学应用题.
例题将一铁块高温熔化后制成一张厚度忽略不计,面积为100dm2的矩形薄铁皮(如图1所示),并沿虚线l1,l2裁剪成A、B、C三个矩形(B、C全等),用来制成一个柱体,现有两种方案:

图1
方案①:以l1为母线,将A作为圆柱的侧面展开图,并从B、C中各裁剪出一个圆形作为圆柱的两个底面;
方案②:以l1为侧棱,将A作为正四棱柱的侧面展开图,并从B、C中各裁剪出一个正方形(各边分别与l1或l2垂直)作为正四棱柱的两个底面.
(1)设B,C都是正方形,且其内切圆恰为按方案①制成的圆柱的底面,求底面半径;
(2)设l1的长为xdm,则当x为多少时,能使按方案②制成的正四棱柱的体积最大?
解析:(1)设所得圆柱的底面半径为rdm,则(2πr+2r)×4r=100,

(2)题意分析:
①本题是由平面图形裁剪后构成的空间几何体,但涉及到的“未知量”较多,且不完全是“相等”关系.
②找出“相等”关系和“不等”关系.
③把条件和结论联系起来,可以从条件入手,向结论转化;也可以从题意入手,挖掘其实际内涵.
④对数学的建模能力和“纯”数学的处理能力要求较高.
方法一:常规思路,从“式子”出发,采用“消元”法.转化为以“x”为“未知量”的分段函数,即以“x”为主元,通过不等关系消去“a”.
如图2所示,设正四棱柱的底面边长为adm,KP=mdm,且已知PN=xdm,QK=4adm,则有100=(4a+m)x.
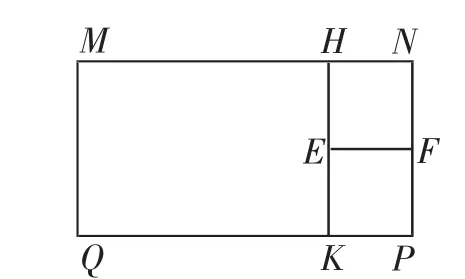
图2


方法二:一般思路,从“式子”出发,采用“主元”法.
转化为以“a”为“未知量”的函数,即以“a”为主元,通过不等关系消去“x”.
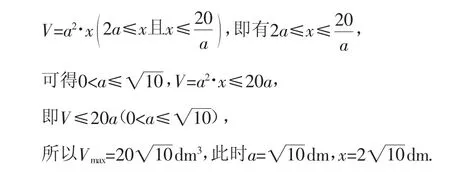
方法三:观察已知式子和所求结论的“结构”特点,进行“配凑”.

方法四:立足“题意”本质,从“意图”出发.

图3
设PK=mdm,已知PN=xdm,且x(m+4a)=100,比较PK与PF的大小,即小的就为正四棱柱的边长.


错因:①学生对平面到空间的转换不适应.②习题的表达过长,让人望文生畏.③题目中变量的关系较多,而且多为“不等”关系,错综复杂.④因变量过多导致关系混乱,不能准确理解题意,不易建模.⑤不等关系不易计算,学生不善于把条件和结论结合起来联想,数学化能力不强,解决数学问题的能力不够.⑥应用题的题意能懂但理解的不够透彻,缺乏耐心和提取关键信息的能力.⑦没有解决应用题的科学习惯,刚粗略读题后就立即书写,没有进行更深层次的思考,实际读题只停留在表面.⑧格式不够规范,没有掌握应用题解题的基本步骤.⑨仍有畏惧心理,“不想做”“不敢做”“不能做”,更不会“分层做”.
(二)近三年高考考题专门研究
研究近三年江苏省高考数学应用题,总结如下:
背景:行程、保护区、公路、仓库、容器等.
知识:三角、圆、切线、解析几何、立体几何等.
考查:解三角形、解析法、求体积、求解析式等最值问题.
方法:找出关系,建构函数模型,利用和积不等式或求导求得最值.
注意:变量的取值范围、习题中的叙述转化为代数式或数量关系;综合性较强,如转化三角形,除了用到正弦、余弦定理外,还会用到两角和与差的三角函数等;先列解析式再通过求导进而得出最值.
二、应用题再认识
1.特点:背景丰富(用概念新颖、取材广泛的实际载体或配图为空间图形和复杂的平面图形等)、文字冗长、变量较多、数量关系复杂(相等和不等关系等).
2.难点:阅读量大、字母多且抽象性高、背景不熟、概念不清、显性关系复杂或隐性关系不明、数学求解不易等.
3.考查要求:阅读能力、创新思维、实践能力、数学类型识别、数学建模、数学思维等综合考查,间接考查数学建模素养、数据分析素养、数学运算素养等.
4.近几年江苏省的考查类型:函数(含分段函数、含范围等)、三角、不等关系、立体几何背景、解析几何背景、物理等学科背景、生活背景等.
三、浅谈应用题的教学策略
1.教会能力
(1)读题能力:对语言进行简化,使题目简明、清晰,可借助表格、图形来处理数据,弄清概念、名词,进一步熟悉和理解背景.一是略读,了解大意,属于哪一类问题,边读边记,边画示意图,防止信息遗漏;二是细读,抓住关键词和重要语句,筛选出有价值的信息,在略读基础上进行研读;三是精读,重在领会,关键把应用题的抽象内容转化为具体内容.要舍得花时间,才能真正读懂、读透,绝不能走马观花就随意动笔.
(2)数学建模能力:即根据题意建立合适的数学模型,把实际问题转化为数学问题,涉及数学抽象能力、挖掘内涵和转化能力等,还涉及:比较、综合、抽象、概况、演绎、推理、联想等能力.
(3)解题能力:针对转化而来的数学问题,选择和运用相应的数学知识解决数学问题的能力,涉及逻辑思维能力、数学运算能力,找准相应解题方法.
(4)计算能力:实际问题的结果都是通过数学运算获得的,需要学生有较高的计算能力.在计算过程中需要学生能灵活应变,化解计算中的难点,同时要兼顾应用题的“实际性”,如自变量的范围、结果的选择等,确保最终答案的正确.
2.教会自主
(1)自主阅读:唤醒学生主动参与,留时间引导学生学会阅读,从慢读、细读、精读、会读,逐步提速,迅速接受概念,快速全面理解题意.
(2)自主提炼:教会学生透过冗长的叙述抓住关键词句,找出重要数据,可以训练学生提炼材料,抓主体保本质.
(3)寻找关系:提炼有价值的信息,找出关系并能等价转化,学会联系,依靠数学知识建立数学模型.
(4)寻找细节:注意细节和特殊条件,应用题的过程和结果离不开实际背景.
3.精心选题 加强系统训练
通过分析近5年江苏高考及全国高考的应用题的特点,编制知识面系统、建模典型的《应用题专题复习》导学案,即按照知识体系对应用题进行分类,对各类模型进行汇总,以培养学生识别模型、建立模型、应用模型的意识和能力,提高教学效益,让学生有法可依.
四、感悟
有位著名的数学家曾经说过:知识不是硬性灌输给学生的,一位优秀的传输者应该积极引导学生进行探索,引领学生进行反思,而不是磨灭学生的创造性和主动性.数学应用题的教学也是如此,它是一个创造、发现、更新并且不断提高的动态过程,我们老师作为高中数学课程的直接建设者与有序引导者,应用题教学的课堂要“慢”下来,教师要善于“引导”、善于“等待”、善于“利用”学生主体,以学生的核心素养为发展核心,逐步提高学生的解题能力.
应用题是高中学生学习的重点,更是学习的难点,难在它的冗长的文字、复杂的数量关系、隐含的关键信息、难以建立的数学模型、关系式的数学处理、格式的规范表达等,这就需要我们数学教师对高中知识涉及的典型应用题进行梳理、对大纲考查的数学模型的情境及种类进行整理,对高中三年的应用题的教学按照所学的知识模块顺序制定一个总体、科学的规划,分期、分阶段逐步、分层实施.同时充分利用课堂这条传授知识和方法的主渠道,引导学生学会思考,学会读题、审题、提取信息;学会建模,学会数学解题,激发学生的主观能动性,培养兴趣和良好的思维习惯;提高学生克服阅读的障碍,敢于阅读、勇于审题、长于转化、善于建模、乐于计算;再是教师要对每一节应用题的教案进行合理设计,着重理解和思维.如果这样坚持下去,经过师生的共同努力,应用题就不再是学生的学习难点,反而会变成一个促进学生建模素养、运算素养等数学核心素养提高的一个落脚点.

