一堂“阿波罗尼斯圆”习题课

☉广西贵港市港南中学 梁志红

“再创造教学”理论最早是由荷兰著名数学家、数学教育家弗赖登塔尔提出来的.笔者认为，在数学教学中引入“再创造教学”很有必要，此举不仅能促进学生的创造性思维的形成，而且能培养其探究数学的兴趣，从而感受数学的乐趣.为此，笔者以人教A版《必修2》第124页习题4.1B组第3题：“已知点M与两个定点O（0，0），A（3，0）的距离的比为，求点M的轨迹方程”为题根，上了一堂“阿波罗尼斯圆”习题课，实录如下，供大家参考.

一、提出问题，引入课题

师：公元前3世纪，古希腊数学家阿波罗尼斯在《平面轨迹》一书中，曾研究了众多的平面轨迹问题，其中有如下结果：到两定点距离之比等于已知数的动点轨迹为直线或圆.

如图1，点A，B为两定点，动点P满足PA=λPB，则当λ=1时，动点P的轨迹为直线；当λ≠1且λ＞0时，动点P的轨迹为圆，后世称之为阿波罗尼斯圆.师：请同学们尝试证明这个结论.

学生自主证明，老师巡视，七分钟过后，发现约九成学生已经完成，于是让学生1利用实物投影仪来展示自己的解答，解答如下：

证：设AB=2m（m＞0），PA=λPB.以AB的中点为原点，直线AB为x轴建立平面直角坐标系，则A（-m，0），B（m，0）.

图1

当λ=1时，x=0，轨迹为线段AB的垂直平分线；

师：在证明过程中，你用的是什么方法？又体现了哪些基本的数学思想？

学生1：这种证明方法叫作解析法，即用代数方法来解决几何问题，在解题过程中用了数形结合思想、方程思想和分类讨论思想.

教学感受：把问题抛给学生，让学生自己完成，老师适当点拨，体现了学生是课堂教学的主体和教师是课堂教学主导的教学原则.

二、给出例题，引导解决

师：下面我们来研究一个与此相关的问题.

例已知圆O：x2+y2=1和点A，点B（1，1），M为圆O上动点，则2|MA|+|MB|的最小值为______.

请同学们观察并思考，在这个问题中是否隐藏着一个阿波罗尼斯圆呢？

起初，许多学生感觉此题与阿波罗尼斯圆没有关系，突然学生2表情兴奋，似乎发现了什么，老师请他回答.

学生2此言一出，部分学生会心一笑，也有学生一头雾水，于是老师请大家互相交流，相互启发，3分钟过后，大家都弄清了本题的解题思路，于是教师请大家规范解答，解答如下：

图2

由题意可得圆x2+y2=1是关于点A，C的阿波罗尼斯圆，且λ=.

设点C的坐标为C（m，n），M（x，y），

所以点C的坐标为（-2，0）.

所以2|MA|+|MB|=|MC|+|MB|.

因此当点M位于图2中的M1，M2的位置时，2|MA|+|MB|=|MC|+|MB|的值最小，且为.

教学感受：本环节给出的例题具有一定的难度，遵循了“跳一跳摘苹果”的教学原则，从中让学生感受成功的喜悦.

三、联系高考，问题再探

师：高考数学试卷中，我们经常可以见到阿波罗尼斯圆的一般形式，阿波罗尼斯圆是一个重要的题根，在历年高考中频频出现.那么，“阿波罗尼斯圆”会涉及哪些问题呢？请同学们回顾以前做过的题目，并举例说明.

学生查阅资料，互相讨论，合作学习，十分钟后交流.

学生3：我找到了一个与圆有关的面积问题，同时也是2008年江苏高考题.

例1满足条件AB=2，AC=的三角形ABC的面积的最大值是______.

解：以AB的中点为原点，直线AB为x轴建立平面直角坐标系，则A（-1，0），B（1，0），设C（x，y），由

两边平方并化简整理得y2=-x2+6x-1=-（x-3）2+8≤8，所以

学生4：我找到了一个与圆有关的参数范围问题.

例2在平面直角坐标系xOy中，设点A（1，0），B（3，0），C（0，a），D（0，a+2），若存在点P，使得，PC=PD，则实数a的取值范围是______.

解析：设P（x，y），则，

整理得（x-5）2+y2=8，即动点P在以（5，0）为圆心，为半径的圆上运动.

另一方面，由PC=PD知动点P在线段CD的垂直平分线y=a+1上运动，因而问题就转化为直线y=a+1与圆（x-5）2+y2=8有交点.

学生5：我找到了一个与圆有关的探索性问题.

例3已知⊙O：x2+y2=1和点M（4，2）.

（1）过点M向⊙O引切线l，求直线l的方程；

（2）求以点M为圆心，且被直线y=2x-1截得的弦长为4的⊙M的方程；

（3）设P为（2）中⊙M上任一点，过点P向⊙O引切线，切点为Q.试探究：平面内是否存在一定点R，使得为定值？若存在，请举出一例，并指出相应的定值；若不存在，请说明理由.

（限于篇幅，本例解答略）

师：很好！同学们集思广益，收获不小.

教学感受：本环节的目的是启发学生利用新知识，温习老问题，重新认识解题方法，从而让思维得以螺旋式上升.

四、再创习题，激活思维

师：刚才同学们发现了与阿波罗尼斯圆有关的三类典型问题，即与圆有关的面积问题、参数取值范围问题和探索性问题.下面，请同学们利用5分钟的时间从三类题中任选一类加以变式，无需解答，然后交流.

（老师巡视，请变式比较成功的学生交流）

学生6：我对例1进行了修改.

例1变式1：在△ABC中，边BC的中点为D，若AB=2，，则△ABC的面积的最大值是______.学生7：我也对例1进行了修改.

例1 变式2：如图3，在等腰△ABC中，已知AB=AC，B（-1，0），AC边的中点为D（2，0），则点C的轨迹所包围的图形的面积等于______.

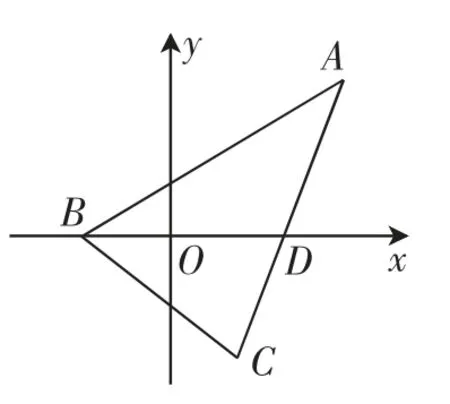
图3

学生8：我对例2进行了改造.

例2变式：在平面直角坐标系xOy中，点A（0，3），直线l：y=2x-4.设圆的半径为1，圆心在l上.若圆C上存在点M，使MA=2MO，求圆心C的横坐标a的取值范围.

学生9：我对例3进行了改造.

例3变式：已知定点O（0，0），点M是圆（x+1）2+y2=4上任意一点，请问是否存在不同于O的定点A使得为常数？若存在，试求出所有满足条件的点A的坐标；若不存在，请说明理由.

师：刚才几位同学的变式相当成功，大家鼓掌！（学生鼓掌）

师：本节习题课，我们围绕着阿波罗尼斯圆展开了讨论，经过讨论发现阿波罗尼斯圆就隐藏在我们平时所做的习题中.当题目中出现“到两定点距离之比”时，我们应该想到阿波罗尼斯圆.本节课的作业就是请大家完成刚才四位同学给出的四道变式题.

教学感受：在学生理解知识的基础上，让学生把例题再创造，可以把学生的思维推向高潮，尤其是对成功者，能充分感受到其中的乐趣，从而更加热爱数学.与此同时，让学生出题，又让学生完成自己出的题，进一步体现课堂教学中学生的主体性.通过本节习题课的教学，笔者深感习题课并非是知识与方法的再现，而是“温故而知新”，习题课应该为学生提供更多探究问题的渠道和空间，从而培养他们的探究能力，这样的习题课才是有意义的.