基于核心素养的高中数学史教学实践探究

☉重庆市永川北山中学校 黄基云

张国定的硕士学位论文《数学史融入数学教学的实践研究》中鉴定了数学史的内容包括数学概念、数学定理与方法、数学家、数学美学、数学名题、数学游戏、数学名著等七个部分，高中数学是围绕高考这个目标进行学习的，故把数学游戏的内容提升为高考数学研究，数学高考史是中国数学发展史的一个重要组成部分.《普通高中数学课程标准（2017年版）》提出高中数学的学习应掌握数学抽象、逻辑推理、数学建模、直观想象、数学运算和数据分析这六大核心素养，高中数学史的学习也是围绕六大核心素养全面展开的，下面将立足于数学核心素养，以探究高中数学史的教学实践.

一、在数学概念教学中感知数学核心素养

数学概念的学习是高中数学的重要内容，很多学生对数学知识似懂非懂以及数学概念挖掘得不够透彻，有些概念的引入是为了解决新的数学问题，例如对数函数的引入是为了解决指数方程解的问题，而有些概念的引入是知识体系的来源，例如椭圆概念形成的过程就是椭圆的定义，这些数学概念的教学既对学生的数学核心素养有一定的要求，又可以进一步提升学生的数学核心素养的深度，下面以椭圆概念作为教学实践研究.

（一）教学引入

教师：同学们，让我们一起复习一下初中学习的圆的定义.

学生：平面内到一个定点的距离等于定长的点的轨迹是圆.

教师：很好，让我们一起思考一下，如果把一定点变为两定点，到两定点的距离之和等于定长的点的轨迹是什么？

图1

（二）实验探究

教师：同学们，想知道到两定点的距离之和等于定长的点的轨迹是什么吗？让我们一起来做个实验求证一下，（1）取一条定长的细绳；（2）把它的两端都固定在图板的两定点处，此时绳子的长度大于两定点的距离；（3）套上铅笔，拉紧绳子，移动笔尖，观察笔尖的轨迹是什么？（教师拿出自制的简易教学道具，请同学上台实验，随着学生慢慢移动笔尖，逐次画出一个椭圆）

图2

学生：移动笔尖，得到的轨迹是一个椭圆.

教学：注意观察此时的细绳的长度与两条线段|PF1|、|PF2|之间有什么关系？

学生：细绳的长度=|PF1|+|PF2|.

教师：即到两定点的距离之和等于定长的点的轨迹有可能是一个椭圆对不对？那一定是一个椭圆吗？再观察一下上述实验，思考细绳的长度与两定点之间的距离|F1F2|之间的大小关系？

学生：细绳的长度大于|F1F2|.

教师：也就是说细绳的长度大于两点间的距离时，到两定点的距离之和等于定长的点的轨迹是椭圆，那细绳的长度如果等于两定点之间的距离|F1F2|，得到的轨迹还是椭圆吗？让我们再用实验验证一下（教师拿出一个细绳的长度等于两定点的距离的道具，请同学上台进行实验，随着笔尖的移动，学生画出一条线段）

学生：当细绳的长度等于两定点之间的距离|F1F2|时，得到的轨迹是一条线段.

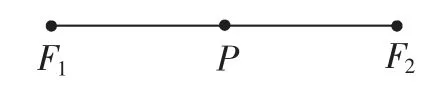
图3

教师：所以到两定点的距离之和等于定长的点的轨迹是椭圆是有条件的，让我们一起来总结一下有哪些条件？

学生：定长的距离大于两定点之间的距离|F1F2|时才能形成椭圆.

教师：但是不要忘记开始的条件，故形成椭圆的条件有：①有两个定点，记为F1、F2，两定点间的距离用2c表示，即|F1F2|=2c，②有一个定长，记为2a，即2a=|PF1|+|PF2|，③最重要的是定长的长度要大于两定点间的距离，即2a＞2c.

教师：让我们一起看课本上对椭圆所下的定义，是否就是我们实验探究得到的形成椭圆的条件？

……

上面这个教学实践从复习引入出发，根据逻辑并大胆推理——到两个定点的距离之和等于定长的点的轨迹是椭圆，再利用数学实验模型对推理的内容进行一一探究，得到到两个定点的距离之和等于定长的点的轨迹可能是椭圆，也可能是线段，利用数据分析整理出形成椭圆的三个条件，最后利用数学抽象对实验所得到的点的轨迹总结并归纳出椭圆的定义，在这一教学实践中，要求学生具备基础的数学核心素养技能，这样学生的数学核心素养能力才可以在这一系列的推理——实验——抽象出概念的过程中得到提升.

二、在数学定理与数学方法的演绎中领悟数学核心素养

数学定理和数学方法是解决数学问题的重要手段之一，也是应用数学的思路保证，学生要达到知其然更要知其所以然的目的，就必须掌握数学定理和数学方法的演绎，在数学定理和数学方法的演绎过程中各个核心素养之间的融会贯通，更是助其数学素养得到进一步提高的关键.例如在立体几何中的向量方法教学过程中，在学习直线的方向向量和平面的法向量概念之后，引导学生推导出利用向量方法解决线线角、线面角、面面角的数学方法，其具体演绎如下：

相关概念：①直线的方向向量：空间直线的方向用一个与该直线平行的非零向量来表示，该向量称为这条直线的一个方向向量；②平面的法向量：直线l⊥α，取直线l的方向向量a，则向量a叫做平面α的法向量.

图4

线线角——空间中异面直线所成的角，如图4所示：

方法：找到这两条直线的方向向量，则向量的夹角即为线线角或者线线角的补角.

线面角——空间中线和平面所成的角，如图5、图6：

图5

图6

通过作图发现直线的方向向量与平面的法向量的夹角有上述两种情况，

第一种情况为向量的夹角与线面角是互余的关系，所以有sinθ=|cos〈a，n〉|，

即线面角的正弦值=向量的夹角的余弦值的绝对值.

综上可证得：线面角的正弦值=向量的夹角的余弦值的绝对值，即sinθ=|cos〈a，n〉|.

面面角——空间中两个平面所成的角，如图7所示：

图7

方法：分别找到两个平面的法向量n1，n2，则两个法向量的夹角为两个平面所成的角或者所成角的补角.

在上述教学过程中，教师要指导学生利用逻辑推理并推理出向量的夹角和线线角、线面角、面面角之间的数学关系，再指导学生利用数学抽象，从图形中抽象出方法并进行总结，建立空间直角坐标系的模型来解决数学问题，然后对空间坐标系下点的坐标等数据进行详细地分析，最后利用数学运算把式子和结果运算出来，这一过程的教学，不仅提高了学生数形结合的能力，而且学生各方面的素养都得到了加强.

三、在对数学家的研究中植入数学核心素养

我国数学发展历程十分曲折，从古至今有很多数学家为了中国数学的发展付出了毕生的精力，所以对数学家的研究是数学史教学中不可或缺的一个重要组成部分，在教学过程中，可以给学生介绍人民的数学家——华罗庚，他自学成才的故事可以用来激励害怕数学运算的孩子们，他的“苏家驹之代数的五次方程式解法不能成立之理由”的论文可以用来激励孩子们勇攀数学的高峰.还有很多数学家呕心沥血研究的数学史记，这都是数学史教学的重要内容，这些数学家的奋斗史可以激励学生不畏数学困难，敢于一头扎进数学的学习中，从而为学生的数学核心素养的提高发挥重要作用.

四、在数学名著阅读中感受数学核心素养

高尔基说过，书籍是人类进步的阶梯，数学发展的每一次飞跃，都离不开书籍的帮助，特别是高中学生要面对高考的压力，要想帮助学生在高考的数学学科中考出理想的成绩，则在教学过程和日常生活中时刻渗透数学名著的重要性，介绍给学生一些数学名著，让其在学累之时读一读，助其感受数学大师们的数学素养风采，感受数学的无穷魅力，让学生在阅读数学名著中爱上数学，在阅读数学名著中感受数学核心素养.