从“云山雾罩”到“豁然开朗”——绝对值函数双重最值问题探究

☉郑州外国语新枫杨学校 何培铤

“疑问”是点燃智慧的火种，诱发思考，激发学生用自己的思维去获取知识，多角度探索思考，对提高解题能力有巨大的推动力.纵观近几年的高考试题，有关含绝对值函数的双重最值问题层出不穷，它与函数、不等式、分段函数等交汇出现，其特点是立意新颖、综合性强、难度系数大，对学生的能力要求非常高.在高三复习过程中，含绝对值函数的双重最值问题高频出现，笔者通过这一典型题类对其进行探究梳理.

一、参数赋值，尝试逐步解惑

双重最值问题通常带有几个参数，再加上绝对值，更让人望而生畏.而数学的本质往往是简单的，越是简单越是接近本质.首先是审题问题，如何理解题中所描述的条件呢？

多元变量造成学生思维混乱，解题困难的局面，为了理清题中描述的条件，对其部分参数字母a，b赋值，转化为一个变量x的函数问题，先把不含参数的函数f（x）理清，再随着a，b的不同赋值，观察对函数f（x）的影响，逐步解惑.也体现了将数学问题化整为零、化繁为简的解题原则.

第一步：我们给定具体的a，b来加以理解：

取a=1，b=0.

再取a=2，b=1.

第二步：加了条件对任意的正实数a和实数b，又是什么意思呢？

不同的a，b，有不同的最大值M（a，b），问题化为对任意的正实数a和实数b，m≤M（a，b）恒成立，所以要求M（a，b）的最小值.所以设f（x）的最大值为M（a，b），问题等价于x∈［1，2］时求M（a，b），再求M（a，b）min.

通过对字母参数a，b赋值发现：（1）对自变量x∈［1，2］而言，求函数f（x）的最大值；（2）从不同的赋值中发现随着参数a，b的不同，函数f（x）的最大值是变化的，函数f（x）的最大值是关于a，b的函数，记为M（a，b）；（3）对任意的正实数a和实数b恒成立，即求M（a，b）的最小值.

通过赋值，快速地判断出各参数对函数f（x）的变化趋势的影响，帮助理清如何针对函数变量和各参数逐步求出函数的双重最值.本题综合性非常强，对学生的要求也非常高，那么如何利用已有的知识构建模式，达成目标.

二、系统函数思想，利用数形结合，实现“融汇贯通”

要解决绝对值函数f（x）的最值问题，先明确函数f（x）的取值范围问题.

先求u（x）的取值范围.

当x∈［1，2］时，因为a＞0，函数u（x）单调递减，所以1-2a-b≤u（x）≤2-a-b.

根据u（x）的取值范围，讨论f（x）=｜u（x）｜的最大值，围绕参数a，b求绝对值函数f（x）的最值问题.下面笔者利用函数思想的各种解题方法对其探究.

1.分类讨论，借助线性规划

根据绝对值的代数意义，关键先明确函数f（x）的最大值和最小值，对参数a，b取值范围进行分类讨论，此类解题方法对学生的条理性、缜密性提出了很高的要求.

显然M（a，b）=max{｜1-2a-b｜，｜2-a-b｜}.

（1）若｜1-2a-b｜≤｜2-a-b｜，即｜1-2a-b｜2≤｜2-a-b｜2，

借助线性规划知识求M（a，b）min.

图1

图2

（2）若｜1-2a-b｜＞｜2-a-b｜，

图3

含绝对值的函数本身就是分段函数的缩影，利用绝对值的非负性，只要对其端点的绝对值比较大小即可，大大降低了类的种数，从而降低了解题的难度.在求M（a，b）min的过程中，利用了线性规划.不等式求最值问题对学生而言，始终是一个难点，而线性规划知识点较为简单，学生掌握程度高，将不等式问题转化为线性规划求最值问题，避免了难而繁琐的计算，快速地完成解题.在教学过程中，重视学生的知识迁移、灵活运用的能力.

2.利用绝对值的几何意义，关注临界状态

含绝对值的函数蕴藏着“距离”的几何特征，解题过程中尽可能利用绝对值的几何意义，利用“1-2a-b，2-ab”随着变量b的变化趋势中形的变化，1-2a-b，2-a-b的值的变化.

因为1-2a-b≤u（x）≤2-a-b，所以u（x）max-u（x）min=a+1.

下面通过考虑b变化的几何意义解决问题，

考虑到b变化，引起函数u（x）图像上下平移，

但是u（x）max-u（x）min=a+1不变，

结合图像即图3，当u（x）max=-u（x）min时，M（a，b）最小，即

本题具有u（x）max-u（x）min=a+1，可以通过b的变化，绝对值的非负性质，对应到图像中的翻折概念，观察判断可得当｜1-2a-b｜=｜2-a-b｜时，M（a，b）取到最小值.与分类讨论比较，利用函数的形，更直观解决函数的最值问题，避免了分类讨论.

三、变式探究，实现触类旁通

经典母题中，给出参数a＞0，使得u（x）在定义域内单调递减，直接求出u（x）的值域，那若a∈R呢？利用函数思想，对所含参数引起的各种可能逐一分类讨论，无疑降低了解题的成功率.本题利用函数思想和绝对值的几何意义，通过数形结合，优势十分明显.

变式：函数，若对任意的实数a和实数b，总存在x0∈［1，2］，使得f（x0）≥m，则实数m的取值范围.

解：由

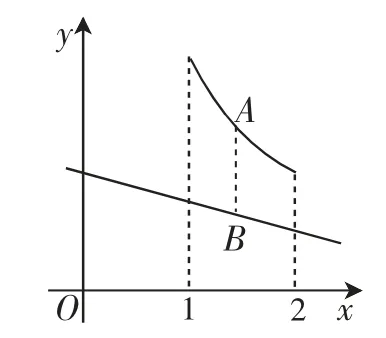
图4

M（a，b）的几何意义是：x∈［1，2］时，｜AB｜的最大值，如图4中，当x=1时｜AB｜最大，要求M（a，b）min的几何意义是：寻找直线的合适位置，使｜AB｜的最大值最小.

如图5中，l1变为l2时，明显的，M（a，b）变大.

那么，最适当的直线位置在哪呢？

图5

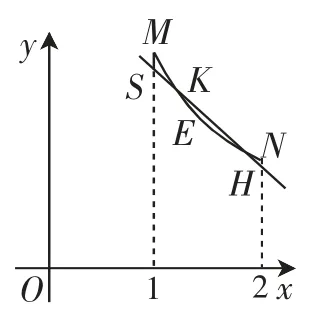
图6

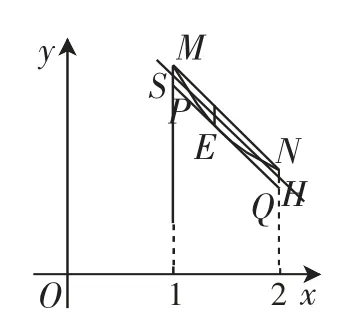
图7

若|MS|=|NH|≠|KE|，则可以通过平移直线l，使max{|MS|，|KE|}变小.

如图7，此时，平移直线MN到PQ，使直线PQ与函数g（x）=，x∈［1，2］的图像相切，切点为E，不妨设P，Q在直线x=1，x=2上，则直线l是平行四边形MPQN的一条中位线，这就是使|AB|的最大值最小的直线位置.

因为对直线l平移和转动，都会使|MS|，|KE|，|NH|中的某一值变大.此时，kMN=-1，

对于多参数绝对值函数模型，如果一味地针对“原函数”分层解决，多层次分类讨论，学生对此问题的解决是望而生畏的，结果很难达到目的.充分利用绝对值的几何意义，转化为两个函数图像之间的距离模型，快速准确地把握图像的关键特点，找到解题的突破点，顺利地避开计算，提高解题的成功率.

波利亚曾说：“对于一个特例之所以要进行这样周密的描述，其目的就是为了从中提出一般的方法的模式.”笔者试着从一题出发，对函数思想、不等式思想、解题模型的综合问题进行梳理，以期达到触类旁通，融汇贯通的效果.