高中解析几何定元素相关问题的解题策略的思考*

☉江苏省南通中学 陆王华

定直线、定点、定曲线这些定元素在某些量的变化下仍会保持确定的特性与状态，这种事前不知道且不受某些量变化影响的特点往往会增加解题的盲目性与解题的难度.

以下是求解此类问题的实际案例.

策略1：运用取特殊值、特殊位置的方法对定直线、定点、定曲线进行探寻并证明其满足一般情形.

例1已知抛物线C的顶点与坐标原点重合，准线l的方程是x=-2，点P在准线l上，纵坐标是（t∈R，t≠0），点Q在y轴上，纵坐标是2t.

（1）试求抛物线C的方程；

（2）求证：直线PQ一定和一个圆心在x轴上的定圆M相切，请同时求出圆M的方程.

解：（1）抛物线C的方程是y2=8x.

考虑特殊情形，取t=1，则直线PQ的方程是y=2，因此定圆M的半径r=2；再取，则直线PQ的方程是3x-4y+4=0.由题意可得，定圆M的圆心M（x0，0）到该直线的距离是2，即，解得x0=2或（不满足一般情形，即圆心到直线①的距离不恒等于2，因此舍去）.

因此定圆M是（x-2）2+y2=4.

该圆满足一般情形的证明如下.因为圆心M（2，0）到直线①的距离（与t无关）.

因此直线①一定和定圆M：（x-2）2+y2=4相切.

评注：对第（2）小问进行思考，不难发现其本质为探寻某个定圆M和动直线PQ一定相切.首先在直线系①中取t=1、t=并得出定圆，然后对该定圆M和直线系①相切进行证明，需要注意的是，t的取值应方便计算.

图1

例2如图1，已知平面直角坐标系xOy中，椭圆的左、右顶点分别是A、B，右焦点是F.若过点T（t，m）的直线TA、TB和椭圆分别相交于点M（x1，y1）、N（x2，y2），其中m＞0，y1＞0，y2＜0.

（1）设动点P满足PF2-PB2=4，则点P的轨迹如何？

（2）设x1=2，x2=，则点T的坐标如何？

（3）设t=9，求证：直线MN必过x轴上某定点（其坐标和m无关）.

解：（1）点P的轨迹是直线x=.

当直线MN和y轴不平行时，可以证明点D（1，0）始终在直线MN上.

因此直线MN必定经过x轴上的定点D（1，0）.

评注：考虑动直线MN和y轴平行的情形可得直线MN必定经过定点D（1，0），再证明其在直线MN上即可.

上述在“动”、“定”之间转换的两个实例都是从一般考虑特殊并获得确定的元素，最后再对已经确定的元素满足一般情形进行证明，这种转换对于解题是极为有利的，问题本身也是运用这种转换思想的空间与平台.

策略2：建立相关函数的解析式并根据题意可得该函数值恒为定值，则其为常数函数并由此获得确定定元素的最直接条件.

例3已知椭圆C：（a＞b＞0）的离心率是，其左、右焦点分别是F1、F2，点P为坐标平面内一点，且，O是坐标原点.

（1）求椭圆C的方程；

图2

解：（1）椭圆C的方程为.

设A（x1，y1）、B（x2，y2），则x1+x2=，x1x2=.

假设y轴上存在定点M（0，m）满足题设，

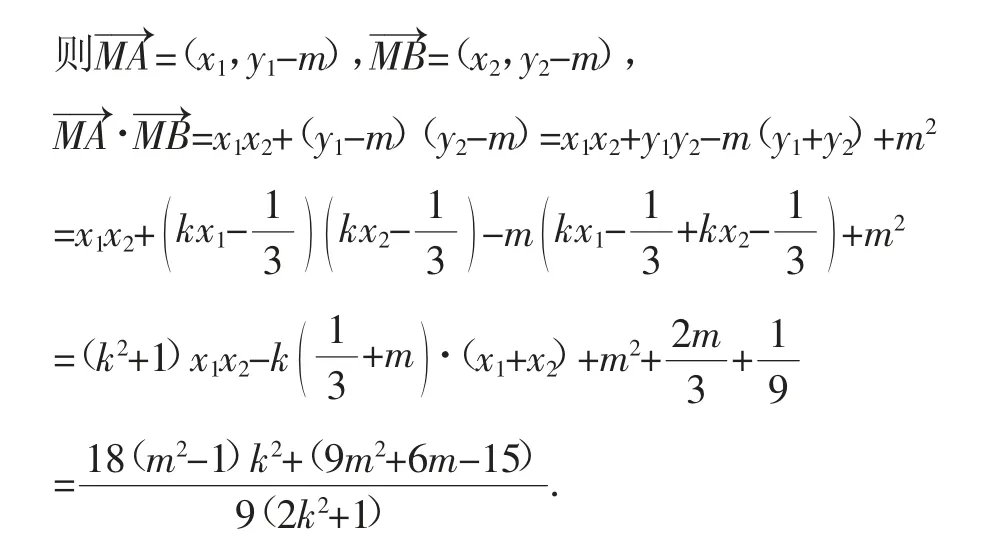
因为假设点M（0，m）满足题设，也就是说对任意的实数k都有恒成立，即18（m2-1）k2+（9m2+6m-15）=0对k∈R恒成立.

因此在y轴上存在定点M（0，1），使以AB为直径的圆恒过定点M（0，1）.

评注：直线l为绕定点S转动的动直线，因此斜率k是变量.列出以为因变量、k为自变量的函数解析式，其中m待定.由函数值恒为0可得出确定m的方程组.运用策略1解决此题同样可行.

在问题的解决中预先制定可能出现的问题的解决方案就是“策略”，事实上，根据形势的变化与发展还会进行方案的调整并落实新的方案，最终在实践、调整、改善中实现目标.解析几何试题一直是高考命题中的重点和热点，函数、不等式、三角、数列等知识以解析几何为载体都会得到综合的应用，涉及较多知识点的解析几何试题对于考生的解题能力提出了较高的要求，很多学生在一些解析几何试题面前往往会表现得束手无策，半途而废的解题现象也比比皆是.本文所思考的定元素问题一直是解析几何范畴内的重要内容，教师在实际教学中应教会学生通观全局并从局部入手，学会运用整体思维进行问题的解决，从宏观上把握问题并从微观上进行解题的突破，帮助学生在审题与解题思路的探寻上进行有意义的思考并不断克服道道解题难关.

总之，解析几何问题对于学生的解析能力、计算能力、作图能力都能起到很好的锻炼作用.本文结合实际案例详细阐述了高中解析几何定直线、定点、定曲线问题的解题策略与方法，以期抛砖引玉.教师在实际教学中应关注到此类题目的灵活性、大思维量等特点，在数形结合的生动教学中帮助学生掌握解析几何定元素问题的解题策略与思想以促进学生的能力提升.