一道高考题的解法说明及解题反思

☉黑龙江省大庆市大庆实验中学 陈永志

向量作为8个C级要求之一向来是区分考生能力的中坚担当，不出意外的是，在2019年的江苏高考中，向量问题出现在了第12题的位置，这是一个典型中档偏难题的位置.出现在这个位置的问题不仅需要学生掌握局部章节的知识，还需要学生能够将前后的知识点联系起来进行综合性解决.如下，我们将从几个不同的方向来剖析本题，并对其背后的知识点与考查意图作一个简要的说明.

（2019年江苏卷第12题）如图1，在△ABC中，D是BC的中点，点E在边AB上，BE=2EA，AD与CE交于O点则的值是______.

图1

破题：纵观题设不难发现图中共存在六个点，其中A、B、C、D、E五点的相对位置，因题中的比例关系而显得相对确定，所以本题的关键在于确定O点与其他几点的相对位置.

解析（1）：以等分点为基础，构造平行线，利用平行线分线段成比例

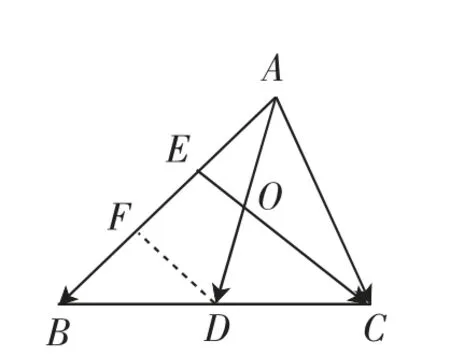
图2

解题反思：平行线分线段成比例是初中几何课程中的重要知识点，同时在高中数学解题的日常中也有较多的应用.这种方法的核心在于能够作出相关辅助线（亦可过D作EC的平行线）.这是用初中知识解决高中问题的典型代表，虽然这可能不是命题人出题的原意，但作为数学课程中的基础性知识，学生应当能够在不同的情境中将其灵活运用.

解析（2）：借助向量共线定理及推论，确定AO与AD的比例关系

引例如图3，A、B、C三点共线，O为线外一点，则

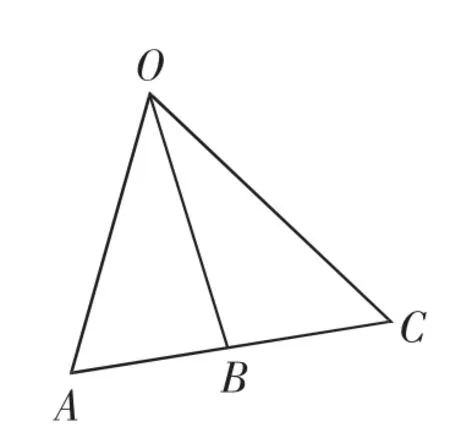
图3

引例解析：不妨设AB=x，BC=y，则由向量共线定理可知，则λ+μ=1.

解题反思：向量共线定理及其推论是高中向量章节的重点内容，它和向量的基本定理、向量数量积的表示是各种类型考试中重点关注的对象.今年高考试卷对共线定理进行考查也在情理之中，翻开前几年的高考江苏卷，不难发现，作为中档题出现的向量问题几乎清一色的是关于向量数量积的内容.因此，从向量共线的角度考虑本题或许正是命题人的根本意图.

解析（3）：借助平面直角坐标系，将点坐标化

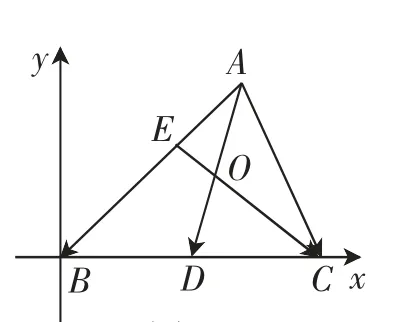
图4

以B为坐标原点，BC为x轴，建立如图4所示的坐标系，不妨设A点坐标为（m，n），E为AB三等分点，则E点坐标为设BC=2，则D点坐标为（1，0），C点坐标为（2，0），则直线AD的方程可表示为，直线EC的方程可表示为，将两者联立解得O点坐标为.故填答案：.

解题反思：要求两条线段的长度之比，一个直接的想法是将其表示出来，那么将三角形置于直角坐标系中是必然的方向，设A点坐标，固定BC长度，将E、O两点及AB、AC两线段用A点坐标表示，根据题设等量关系寻找A点坐标两未知量的关系，利用代入消元法，将待求比例转化成关于m的表达式整体约分得解.当然解析中所用建系是比较一般的建系，我们还可在不改变题意的前提下，将问题特殊化，进行特殊化建系，例如，不妨设AB⊥EC，以E为坐标原点，EC、AB分别为x轴，y轴建立直角坐标系，计算将会更加简练.当然将问题特殊化有一个重要前提即特殊化后的问题情境必须符合原问题，有一个简单的检验方法是特殊化后的计算过程不能与原问题情境相冲突或与特殊化的条件相冲突.

解析（4）：以热点解法极化恒等式为桥梁，并结合解三角形知识进行破题

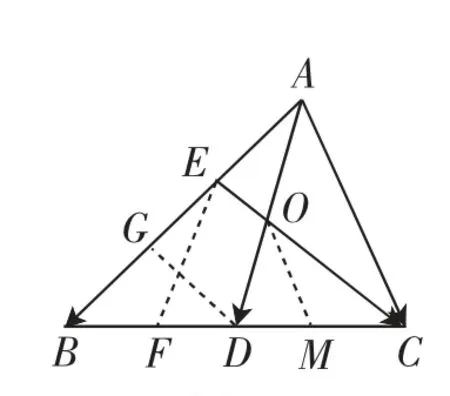
图5

过E作EF平行于AD，过D作DG平行于EC，由解法（1）易知点O为AD的中点，为EC四等分点.取DC中点M并连接OM，由极化恒等式可知，由比例关系知再用一次极化恒等式得，两者相等得AD为三角形ABC中BC边的中线，由必修5第16页例6的中线定理可知代入上式可得AB2=3AC2，即故填答案：.

解题反思：在平时的教学中我们不断给学生建立这样一种意识，在向量数量积问题中凡是涉及中点问题的问题不妨考虑用极化恒等式.虽然本题不是典型的向量数量积问题，但题设中有数量积，又有中点，还有线段之间的比例关系（这点与2016年13题相似），可以考虑从极化恒等式角度对已知等量关系进行转化.与2016年13题利用极化恒等式与线段比例关系可直接求解不同，本题在此基础上还需要借助解三角形中的中线定理实现三个量关系到两个量关系的转变.当然中线定理在高考说明中现已不做要求，在平时的授课中也仅以例题的形式出现，不属于必需掌握的范围，显然，这对于基础好的学生可以挑战，而针对一般学生而言建系或利用基底进行解决才是正途.