一个焦点弦恒等式的应用

厦门大学附属实验中学 (363123)

林秋林

圆锥曲线的焦点弦由于其能与直线的倾斜角、向量(定比分点)、三角形面积等知识交汇，而倍受命题人青睐，因此一直以来都是高考及各级模拟考试的一个热点问题，而且问题难度一般不小．不过在与焦点弦有关的这些问题中，有一些却能够借助一个恒等式较为简便地解决．本文正是通过几个例题向大家介绍这个恒等式的一些简单应用．

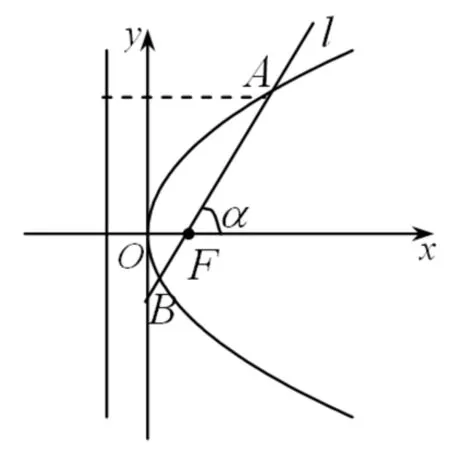
图1

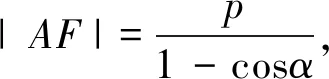
例1 已知抛物线y2=8x的焦点为F，直线l过F且依次交抛物线及圆(x-2)2+y2=1于点A,B,C,D四点，则|AB|+4|CD|的最小值为．(2019年1月福州市高三质检)

图2

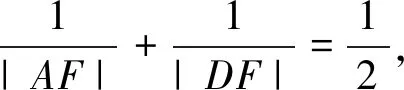
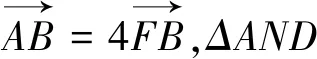
A.y2=xB.y2=2xC.y2=4xD.y2=8x

图3

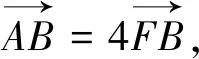
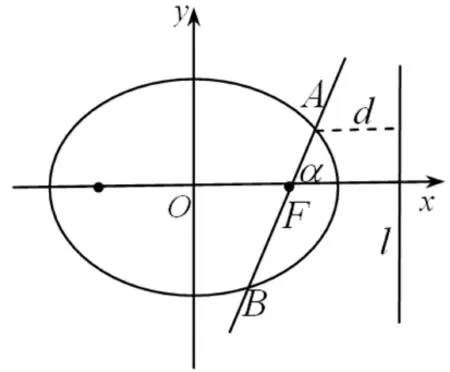
图4

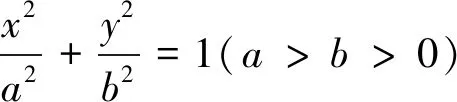
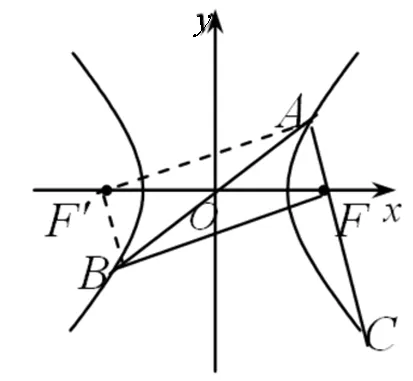
图5

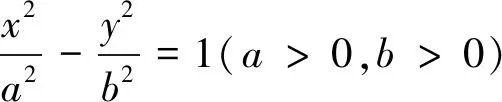
解:设左焦点为F′，则四边形AF′BF为平行四边形．又BF⊥AC，故AF′BF为矩形．记|BF|=x，|AF|=y，则有故由恒等式，可得即解得从而故选A．

图6

该焦点弦的恒等式不仅形式简单，而且在解题中有着无可比拟的作用，不禁让人感受到数学之美．