2019年江西省高中数学预赛一道解几题的多解探究

江西省石城县职业中学 (342700)

温 露

2019年高中数学联赛江西省预赛第9大题是一道解析几何题，试题为：

设椭圆C的两焦点为F1,F2，两准线为l1,l2，过椭圆上的一点P，作平行于F1F2的直线，分别交l1,l2于M1M2，直线M1F1与M2F2交于点Q.证明：P,F1,Q,F2四点共圆．

这是一道以解析几何中椭圆相关性质为题干，证明平面上四点共圆为结论构建的试题，是一道解几与平几结合，考查考生解析计算与演绎论证综合能力的好题，命题者给出的标准答案为：

图1

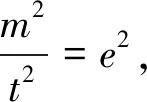
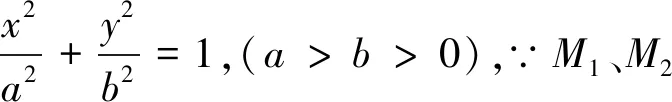
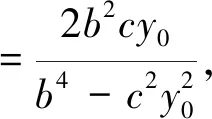
∠F1QF2=180°，∴P、F1、Q、F2四点共圆.

同样的方法，可以证明cos(∠F1PF2+∠F1QF2)=-1,结论得证.

考虑到，在四边形PF1QF2中，PF2所对的角若能相等，则结论也得证，于是可得：

仿照上述思路，我们在四边形中找到多对同弦上的角，均可尝试证它们分别相等，得出所需结论，读者不妨一试.

一道试题，能有如此多的解法，彰显其探究魅力.