平衡系数，柳暗花明

安徽省枞阳县第二中学 (246700) 荣光辉安徽省枞阳县宏实中学 (246700)

江保兵

一、一道竞赛试题和它的解法

这是2018年全国高中数学联赛湖北省预赛第7题，这是一道条件最值问题，题面简洁，内容丰富.从公布的参考答案来看，本题主要考察多元均值不等式的应用.

二、利用均值不等式平衡系数

事实上我们假设存在实数M和λ>0，使得下面这个不等式成立：

我们可以看到，平衡系数法是一种非常精致的待定系数法，系数的确定难度较大，运用的技巧较高，不仅要求熟练地使用代数变形，熟练地使用一些常用的不等式，而且要求这些系数能够和谐地融入一个复杂的环境中，这时我们必须使用额外的变量来求解方程或者方程组找到原始的最终系数，这就是平衡系数法的关键和精髓.

例2 (2017年全国高中数学联赛湖北预赛高一、高二第7题)已知正实数a,b满足ab(a+b)=4，则2a+b的最小值为.

三、利用柯西不等式平衡系数

这是2018年全国高中数学联赛湖北省预赛第11题，试题结构工整、对称，由结构中根号，联想到柯西不等式，相关系数的确定，又想到平衡系数法.

四、利用嵌入不等式平衡系数

这是2018年全国高中数学联赛安徽省初赛第11题，我们现在利用嵌入不等式平衡系数.

首先介绍一下嵌入不等式：设A,B,C为任意三角形的三个内角，x,y,z为任意实数.则有x2+y2+z2≥2xycosC+2yzcosA+2zxcosB.

简证：x2+y2+z2-(2xycosC+2yzcosA+2zxcosB)=(x-ycosC-zcosB)2+(ysinC-zsinB)2≥0.

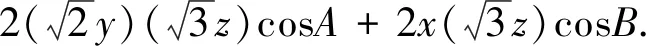
一道好题，犹如一块璀璨的碧玉，让人爱不释手.而对试题的分析、探究更象一次奇妙的精神之旅，精致的解题技巧，丰富的数学思想，不一样的风景，总是让人流连忘返.