平和创新 朴实灵动*——2018年江苏高考数学第13题评析与教学启示

江苏省板浦高级中学 (222241)

李忠贵

高考数学试题凝聚了专家的集体智慧和大量心血，是丰富的“宝藏”.对高考题(特别是压轴题)进行深度研究，有利于领会其命题规律、设计意图、选拔功能，感悟数学的育人价值，从而把握教学的方向，找准教学中存在的问题，实施教学变革，实现高效教学.下面是笔者对一道高考题的深刻思考，期待对今后的教学有所启迪.

一、试题

在△ABC中，角A,B,C所对的边分别为a,b,c，∠ABC=120°，∠ABC的平分线交AC于点D，且BD=1，则4a+c的最小值为．

二、评析

1.试题立意

本题为文理合卷的填空题第13题，为压轴难题，涉及高中数学众多核心(主干)知识，比如基本不等式、平面向量的数量积、角平分线性质、余弦定理、三角形面积计算公式、导数、三角函数定义及性质、同角三角函数关系等，它们在《2018年江苏省数学高考考试说明》中要求均为B、C级要求，凸显了对核心内容重点进行考查的命题思路，彰显了在知识网络交汇处命题的设计理念，考查了数形结合、函数与方程、转化与化归等数学思想以及逻辑推理、数学运算、数学抽象、数学建模等核心素养，充分体现了以考查“核心素养和创新思维”为重点的命题导向，问题构思自然，设计精巧，独具匠心.

2.试题表达

试题以斜三角形和多元函数最值的背景呈现，考生十分熟悉，试题表达清晰，简单明了，降低了阅读量，进而减少了阅读时间和缓解考生的心理压力，这些给考生以简洁中见关怀、平和中见亲切.思考与求解过程中却又能感受到本题的创新之处，这也为优生提供了展示的空间，凸显了压轴试题良好的效度和区分度.

3.试题来源

命题专家以上述必修五两道课本题为蓝本，以斜三角形为载体，进行变式、重组、创新设计，从而得到本试题.

4.试题传承

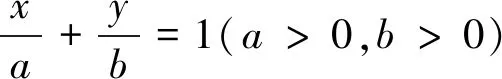
以上题都是多元函数的最值问题，而本试题更灵活、难度也变大，体现了良好的传承.

5.试题解法

从条件和结论的内在联系知，求解分两步：

(1)由已知条件推导a与c相互关系；(2)在此基础上求4a+c的最小值.

第一步：推导a与c的相互关系.

思路一：挖掘图形中隐藏的面积关系，再利用已知条件分别进行表达，则问题可轻松解决.

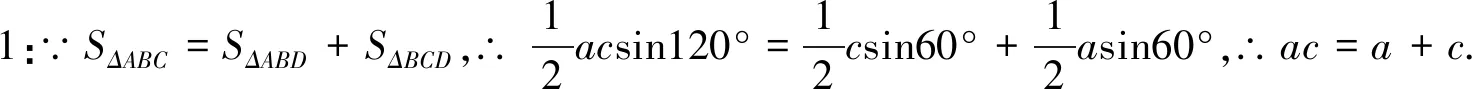
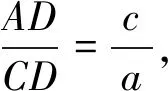
解法2：在ΔABD和ΔBCD中，由余弦定理得

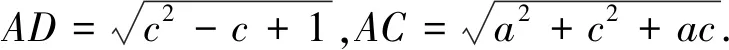
思路三：对于几何图形问题，可利用已知条件恰当建系，运用代数方法进行处理.

图1

图2

思路四：向量的模本质为两点间的距离，向量的数量积活化模的求法.因而可利用平面向量基本定理、向量的数量积及角平分线性质进行转化.

第二步：由a与c等量关系求4a+c的最小值.

思路一：由目标的结构特点，再结合a与c的等量关系，容易联想到基本不等式.而目标为“求‘和’的最小值”，必须合理变形，配凑出“‘积’为定值”.

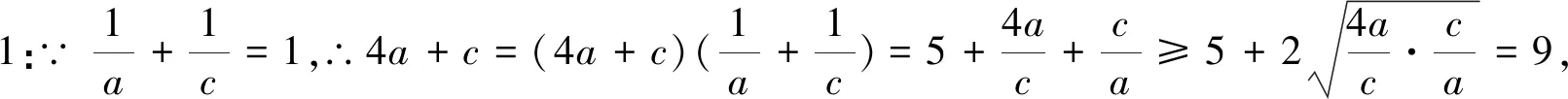
思路二：由a与c等量关系特点，可通过减元或换元，将多元函数化为一元函数，可轻松配凑出“‘积’为定值”，则难点得以突破.

思路三：由a与c等量关系，合理减元，将多元函数化为一元函数.由于此函数不是基本函数，可借助导数确定其单调性，进而求出最小值.

思路四：由a与c等量关系，合理减元后，将函数问题转化为一元二次方程，利用判别式进行求解.

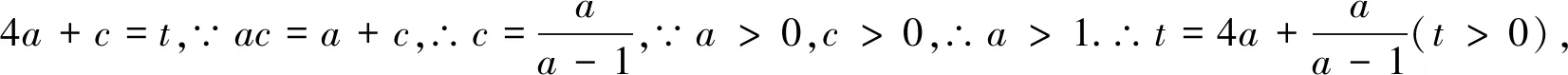
思路五：由a与c等量关系和目标的结构特点，联想到向量数量积性质，从而构造向量进行求解.

思路六：由a与c等量关系和结论的内在联系，联想到柯西不等式，进行求解.

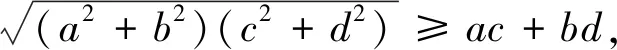
解法反思：

①第一步解法：有的挖掘图形中隐含的面积等量关系，有的利用角平分线性质和余弦定理，有的恰当建立坐标系，有的构造平面向量并利用向量的数量积求解等，以上解法均从核心知识及其内在联系出发，用数学的眼光去思考与求解问题，运用数形结合、转化与化归等数学思想方法实现合理转化，这是求解数学问题的通性通法；

②第二步解法：有的通过“1”的代换、三角换元、均值换元、减元等配凑出“积”为定值，从而使用基本不等式进行求解；有的通过减元，将多元函数的最值问题化归为一元函数的最值问题，使用导数法求解；有的运用函数与方程思想，利用一元二次方程有正根的条件求解；有的巧妙构造平面向量，运用向量的数量积性质，问题可轻松求解；有的根据问题的结构特点，利用柯西不等式等.

以上解法尽显“数学味”，彰显学生的核心素养和关键能力.因而本试题及解法平和创新，朴实灵动.

6.求解陷阱

(1)陷阱之一：方法自然但难以求解.

(2)陷阱之二：两次用公式导致错解.

错因分析：∵不等式(1)等号成立的条件为a=c,不等式(2)等号成立的条件为4a=c，∴两个等号无法同时成立，∴4a+c>8,∴4a+c的最小值不为8.

三、教学启示

1.用好课本例(习)题，揭示其隐含价值

课本是众多专家依据教学大纲反复打磨编写的系统阐明数学内容的教与学用书，它不但是教师教、学生学的关键，而且是各种考试(尤其是高考)试题命题的主要来源.有的教师认为“课本例(习)题简单，难以应对高考，没必要花时间去研究，不如多讲、多练一些教辅资料上难题更实惠”，显然是错误的.教师应深度研究教材，把握编写专家的意图，发挥例(习)题的示范性、典型性，并对其拓展延伸，挖掘其蕴含的教学价值、隐藏的重要结论、数学方法、数学思想、研究方法、数学本质、数学文化、育人价值等，对启迪学生思维、发展学生关键能力、提高数学解题效率等大有裨益.

2．让学生自主建构知识，突出对其本质的探索

高考的压轴题，常常涉及的是多元的概念、原理与公式.如何深刻理解这些知识点，弄清其内在联系，并能创新应用，本身就需要一定的智慧，单靠大量刷题或者死背硬记肯定难以奏效.知识不是教师告诉学生的，也不是学生看书得到的.这就需要教师在教学中恰当创设教学情境、精心设计问题，深度引领学生自主探究，自主建构知识，让学生学习数学的过程变为在教师诱导下“再发现”过程；同时孤立的知识无法形成能力，教师要让学生感悟核心知识的交汇之处，帮助他们建立和体会完善的知识网络体系；为提升学生的应变能力，教学中教师应着力培养他们追问知识及问题本质的习惯.如为什么要学习基本不等式？基本不等式的功能是什么？它的本质是什么?应用它求解问题应注意哪些？...

3.关注核心素养培养，重视学生的感悟反思

无论哪种课型，教师的讲还是学生的练，都需要教师紧扣教学目标，贴近学生最近发展区，运用教学智慧，以素养立意，从整体精心设计.为什么选择这个问题？想培养学生哪些能力？发展哪些核心素养？这种解法如何自然呈现？是否可一题多解？多种解法能否归一？多种解法的本质、核心及其内在联系又是什么？最优解及通性通法又是什么？可否进行一题多变？可否设计多题归一？要谨防教学(特别是高三教学)形式单一化，不是“讲练讲”就是“一讲到底”，或者是“练讲练”，学生疲于应付.因为所有素养和能力的提升最终都要通过学生的自我感悟反思来实现,所以要给学生留有足够的时间和空间，让他们经历理解、反思、总结、提炼、内化、感悟的思维历程.