问题驱动探究，拓展发展素养——“三角形小结复习”教学实录与评析

☉湖北省武汉大学附属外语学校 周一敏

☉湖北省武汉市武昌区教育局教研培训中心 刘 欣

问题驱动是探究式教学的重要手段，而探究式教学是基于核心素养的一种重要教学方式.以培养学生核心素养为依据的教学设计，要合理创设情境，精心设计问题，启发学生探究，发展学生思维，让学生在探究的过程中既掌握知识与技能，又感悟知识的本质，积累思维和实践的经验，形成和发展核心素养.章节复习课是课堂教学中的一种常见课型，在教学中如何将数学学科核心素养落实到课堂，重视和加强数学思想方法的提炼和渗透，有效提升学生的思维水平和数学素养.执教者在2018年9月28日“国培计划”枣阳市送教活动中主讲“三角形小结复习”一课，尝试以问题为主线，以线串珠，驱动学生自主探究，构建知识网络，并通过变式拓展，打破思维定式，逐级推进深度思考，起到了较好的复习效果，获得了同行的一致好评.现将这节课的课堂教学实录整理如下，与同行交流探讨.

一、教学实录与点评

1.巧妙设问，梳理知识

师：本章中我们学习了与三角形有关的线段、角及多边形的内角和等内容.同学们，你能运用所学知识解决下面几个问题吗？

（教师画图，提出问题，学生思考，然后回答）

师：画一个△ABC，若AB=5，AC=3，则BC的取值范围是多少？

生1：2＜BC＜8.

师追问：你是怎么得到的呢？

生1：由三角形的三边关系可得.三角形两边之和大于第三边，两边之差小于第三边，所以AB+AC＞BC＞AB-AC.

师：很好！那么，哪个同学能说说得出“三角形两边之和大于第三边”的依据？

生2：可以把B、C两点看成定点，由“两点之间，线段最短”得到AB+AC＞BC.

师：很好.同理，我们可以得出另外两个不等式.通过移项，不难得出AB-AC＜BC.

（教师在△ABC中继续作图，提出新问题）

师：过点A作AD⊥BC于点D，作AE交BC于点E，使得∠BAE=∠CAE，取BC的中点F，连接AF.你们能在图中分别找出△ABC的高、角平分线和中线吗？

生3：AD是高，AE是角平分线，AF是中线.

师：很好，在研究与三角形有关的线段时，除了三边之间的关系，我们还要能根据已知条件熟练找出三角形的高、角平分线、中线.

师：在△ABC中，若∠A=80°，∠C=60°，则∠B等于多少度？

生4：∠B等于40°.

师追问：你是怎么求出的呢？

生4：根据三角形内角和等于180°，∠B=180°-80°-60°=40°.

师：这名同学说三角形的内角和等于180°，这个结论是怎么证明的呢？

（生5上台演板，作辅助线并说明证明思路，生6补充不同的证法）

师：这两名同学在证明“三角形的内角和为180°”的过程中，都利用了平行线的性质与平角的定义.大家看，我过点A作AH⊥BC，那么∠BAH又是多少度呢？由此可以得出什么结论？

生7：∠BAH等于50°，可以得到直角三角形两个锐角互余.

师：如果把边CB延长，得到△ABC的一个外角∠ABD，则∠ABD的度数是多少？

生8：∠ABD等于140°.

师追问：你是怎么求出的？

生8：根据邻补角的定义可以求出，也可以根据“三角形的外角等于与它不相邻的两个内角的和”求得.

师：你可以由三角形的内角和定理来推出这个结论吗？

（生8叙述证明过程，教师补充并加以评价）

师：∠1、∠2、∠3是△ABC的三个外角，（图略）这三个角的和是多少度？

生9：分别求出三个角，可以得到三个角的和为360°.

师：我们是不是也可以看作三个平角分别减去三角形的三个内角求得呢？

师：三角形是最简单的多边形，也是认识其他图形的基础，我们可以利用三角形的内角和来研究多边形的内角和.在边BC外取一点D，连接DA、DC，构成一个四边形，那么这个四边形ABDC的内角和是多少？外角和是多少呢？

生10：这个四边形的内角和为360°，外角和也为360°.

师追问：能由三角形的有关知识推出吗？

生10：四边形ABDC是由两个三角形△ABC、△BCD组成的，根据三角形的内角和定理可以推出四边形ABDC的内角和是360°，从而得到外角和也为360°.

师：五边形的内角和是多少？外角和是多少？n边形呢？

（学生思考、回答，教师追问并关注学生能否运用自己的语言解释得到答案的过程）

师：我们发现，可以由三角形的内角、外角类比研究多边形，得到多边形的内角和、外角和.

点评：教师画一个△ABC，提出问题，引导学生运用三角形内角和定理解决实际问题，在学生交流三角形内角和定理的不同证明方法的过程中，归纳获取知识的途径、方法、思想，调动学生深度思考.接着在△ABC的基础上，继续画图，提出新的问题，设计一个个问题串，带领学生解决问题，具体、直观，较好地复习了本单元的核心内容、主干知识和重要的思想方法.虽是复习旧知，但不是旧知识的简单再现.这样驱动学生自主探究，促进学生深入思考，激起了学生的学习兴趣.

2.激发思维，构建体系

师：同学们，根据刚才的知识梳理，你能发现本章主要知识之间的联系吗？你能画出本章知识结构图吗？大家动笔试试，然后小组交流.

（学生画知识结构图，教师巡视并关注不同层次的学生，适当进行提示和指导.学生完成后，小组之间相互交流完善，教师利用“希沃授课助手”展示部分学生的结构图）

师：我们来看看这名同学画的结构图.本章主要知识点有哪些？你发现它们之间有什么联系呢？

生11：我觉得本章主要知识点可以分为与三角形有关的线段和角，其中线段有边、高、中线、角平分线，角有内角和、外角和.

师追问：多边形的内角和、外角和与三角形有什么联系呢？

生11：可以通过连接多边形的对角线，转化为三角形问题，进而求解.

师追问：你为什么想到这样列框架图呢？有什么作用呢？

生11：我觉得简洁、明了，可以帮助我熟练运用本章知识解决问题.

师：有没有同学和刚才这名同学思路不一样呢？可以给大家展示一下.

生12：我画了一棵树的形状，以三角形为主干进行发散，在枝干上有线段和角，然后在小分枝上把所有的概念和定义都写了出来.

师追问：你觉得这样画有什么好处呢？

生12：我把所有的概念、定理都画出来了，很全面，可以加深印象，不容易忘记.

师：很好！还有同学有不一样的想法，想要展示或者补充的吗？

生13：因为我觉得图形和符号比文字更简洁，所以我的框架图都是用图形或者符号，便于记忆和理解.

师：大家的想法都很好，画出的框架图也非常棒！在每一章学习结束后，我们要善于对本章知识进行归纳和整理，归纳的方式不唯一，可以用文字，也可以用图形、符号等，重要的是要形成自己的知识体系，进而灵活运用所学知识解决问题.

（学生回答，简要说明自己列框架图的意图，教师给予肯定，学生相互补充完善，师生在黑板上共同完成如下知识结构图）

图1

点评：留给学生充足的时间，让学生自主思考、分类归纳，绘制单元知识树或知识框架图，并让学生交流自己绘制的意图，解释绘图依据，这样的交流活动，梳理基础知识，构建整体知识网络，引发学生深层思维，发展了数学抽象、直观想象、逻辑推理的数学学科核心素养.

3.综合运用，能力提升

师：下面，我们利用本章知识解决一些综合问题.已知等腰三角形的两边长分别为4和8，则这个三角形的周长是多少？

生14：它的周长是20.

师追问：你是怎么得到的？

生14：因为等腰三角形的两腰相等，题中已知两边长分别为4和8，可以分为两种情况：4、4、8和4、8、8，但是4+4=8，即4、4、8不符合三角形三边关系，所以这个三角形三边长分别为4、8、8，周长为4+8+8=20.

师追问：很好.这个问题用到了什么知识？需要注意什么问题？

生14：用到了三角形三边之间的关系，要注意分情况讨论.

师：很好.反之，若等腰三角形的周长为20，一边长为4，则其他两边长是多少？

生15：分情况考虑：若4是腰长，另两边分别是4和12，4+4＜12，不符合三角形三边关系，故应该舍去；若4是底，另两边分别是8和8，4+8＞8，符合三角形三边关系.所以其他两边长均是8.

师：很好，仍然用到了三角形三边关系的知识和分类讨论的思想.现在把这个问题放到实际情境中：小明用一条长20cm的细绳围成了一个等腰三角形，他想使这个三角形的一边长是另一边长的2倍，那么这个三角形各边的长分别是多少？请同学们写出解答过程.

（学生先独立思考，教师巡视，关注不同层次的学生并予以指导.接下来，教师利用“希沃授课助手”展示学生范例，明确所用知识点，强调解题格式，规范书写过程）

师：我们再来看看与三角形的角有关的问题：如图2，在△ABC中，∠ABC、∠ACB的平分线BD、CE相交于点O.若∠ABC=40°，∠ACB=60°，则∠BOC是多少度？说一说你的思路.

生16：∠BOC=130°.因为BD平分∠ABC，所以∠DBC=∠DBA=20°.因为CE平分∠ACB，所以∠BCE=∠ACE=30°.在△OBC中，∠BOC=180°-∠OBC-∠BCO=130°.

师追问：你在解决这个问题的时候，用到了哪些知识？

生16：用到了三角形的内角和、角平分线的定义.

师：现在把条件变一下，若∠A=80°，则∠BOC是多少度呢？谁能解决这个问题？

（生17回答，叙述解题思路）

师追问：你又用到了哪些知识？

生17：用到了三角形内角和定理、角平分线的知识.

师：这里其实还用到了整体的数学思想.当∠A为任意角度时，∠BOC和∠A之间有怎样的数量关系呢？

（学生独立思考，然后回答）

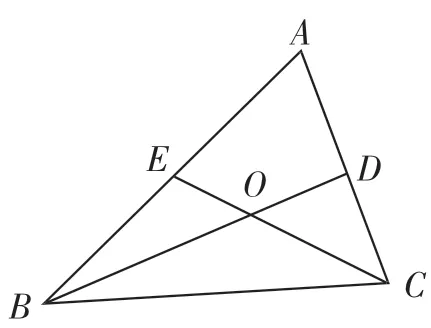
图2

师：其实，用三角形内角和定理和角平分线的知识可以解决这样一类问题，例如：若∠ABC的外角平分线与∠ACB的外角平分线相交于点O，则∠BOC与∠A又有怎样的数量关系？若∠ABC的平分线与∠ACB的外角平分线相交于点O，则∠BOC与∠A又有怎样的数量关系？同学们可以进一步探究.

点评：在原有问题的基础上，进行变式化的问题设计，既激发了学生对问题的探究兴趣，又打破了学生的思维定式，增强应变能力.两个例题的变式拓展，层层推进，引导学生在不同背景、不同层次的问题中逐步把握问题的本质，达到举一反三、触类旁通的效果，培养了学生的逻辑推理能力.

二、评析

《义务教育数学课程标准（2011年版）》指出：“动手实践、自主探究与合作交流是学生学习数学的重要方式，数学学习活动应当是一个生动活波的、主动的和富有个性的过程.”本节课设计严谨，过程流畅，问题的提出与解决环环相扣，数学活动的开展井然有序，较好地体现了新课程的教学特点.课堂中充分体现了学生的主体地位，教师只是学习的组织者、引导者、合作者，学生在解决问题的过程中，体验了构建知识体系的过程，探寻了解决问题的方法，经历了展示交流的成功喜悦.

1.以“问题驱动”为主线

本节课教学中，从一个基本图形三角形出发，添加线段构成新的图形，精心设计一系列问题，将要复习的核心知识隐含于问题中，然后引导学生一个个逐步解决，在解决问题的过程中，让学生脑子里形成知识网络，从而自主构建知识框架图，并在此基础上将问题拓展延伸，让学生在解决综合问题中，发展思维，提升能力.教学活动围绕“问题驱动—构建体系—应用探究—归纳总结”几个环节展开，把教学内容转化为问题，并以问题为线索，引导学生发现问题、分析问题、解决问题，为学生创设了和谐的、自主探究的课堂学习环境，问题层层推进，满足了不同发展潜能学生的学习需求.

2.以“展示生成”为方法

在进行知识梳理和构建知识网络图的过程中，组织学生交流展示，教师留给学生充足的时间，给学生提供了更多的合作与交流的机会，让每个学生都积极参与到学习中来，都有自由表达的机会.课堂中教师的很多追问是根据学生的回答即时生成的，学生的回答也展示了每个学生思维的敏捷和智慧.这样的课堂教学组织让学生的学习从“被动式、接收式”变成“自主式、合作式、探究式”，培养了学生“在探究知识发生、发展过程中学习知识”的学习习惯，让学生学会学习、学会思考、学会探究、学会建构，让学生在交流、表达、展示中获得了成功体验，激发了学生的深度思考，在具体的数学活动情境中，学生的数学素养自然生成.

3.以“发展素养”为核心

数学学科核心素养是学生在学习数学的过程中逐步形成的综合能力，它基于知识和技能，但高于数学知识和技能.要使学生在真实的情境里，通过自主学习、合作学习和研究性学习，主动进行知识建构，逐步建立认识、理解、解决问题的思想方法和策略，形成核心素养.教学中教师从学生现实生活的经历和体验出发，让学生经历“发现问题—解决问题—提出问题—解决新问题”的学习过程，整理本章知识，思考知识之间的联系，形成知识体系，体会研究几何问题的一般思路和方法，从而能够有条理地思考、解决问题，能够在较复杂的问题情境中运用所学图形的性质解决问题，发展了逻辑推理能力.课中基于数学学科核心素养的问题设计，课堂教学中充分体现学生主体地位的展示平台，实现了师生互动、生生互动，在一系列具体的数学活动中，体现了以“发展素养”为核心的宗旨，学生的数学学科核心素养在学习中得以充分发展.