借助辅助圆 搭建动态最值问题求解桥梁

周志韧

(上海市同济大学附属实验中学 201805)

初中数学中的很多几何问题，看似与圆没有任何关系，但是借助已知条件恰当构建辅助圆，常常可以实现问题的简单化和简洁化，让解题思路豁然开朗.究竟如何发现圆、何时构建圆是关键问题，本文就结合例子详细讲解.

一、借助圆的定义，构建辅助圆

圆的定义告诉我们，圆心到圆上任意一点的距离都相等或者是到圆心距离都相等的点在圆上.当问题中涉及运动过程，涉及到某一定点且某一线段的长度保持不变时，可以尝试构建圆，借助圆的性质进行求解，如：

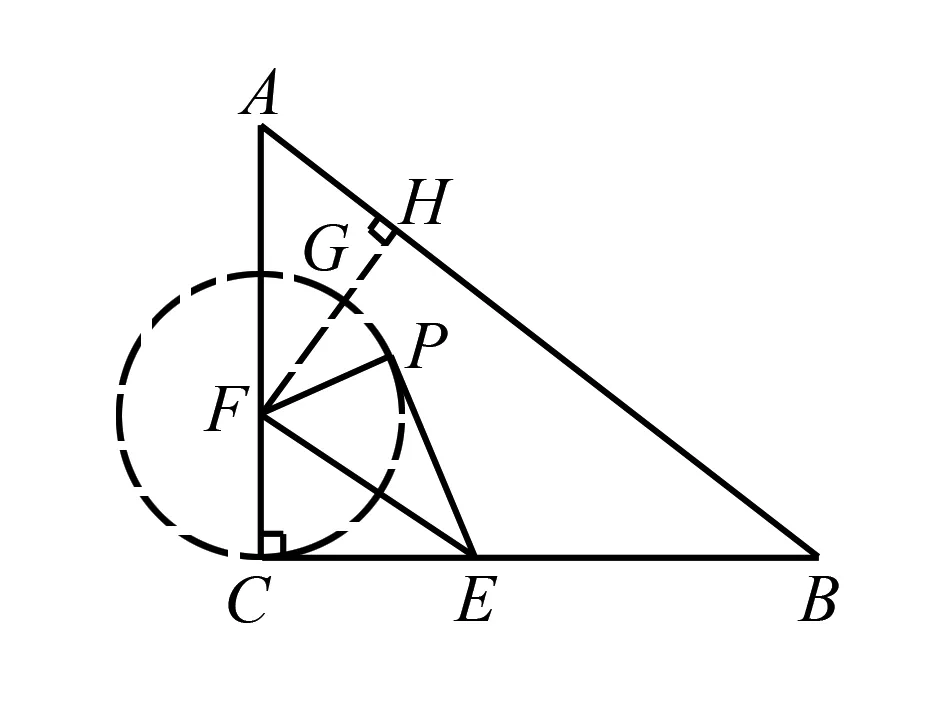
图1

例1如图1，已知△ABC是直角三角形，∠C=90°,AC=6,BC=8，边AC上有一点F，满足CF=2，边BC上有一动点E，现将△CEF沿着直线EF进行翻转，使得点C落在P，则点P到边AB最小距离是( ).

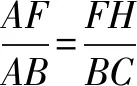
反思借助已知条件将点到边的距离转化为圆上某点到某边最短的距离，实现了原问题的转化，实现原问题的难度降低.转化的关键在于能够准确把握已知条件实现知识的迁移和转化.

二、借助圆切线寻找相关量的关系，构建辅助圆

结合圆的切线和三角函数的关系，可以知道圆O外一定点A，与圆外一动点P，当AP与圆相切时，∠PAO取得最大值.借助此特性，可以解决某类最值问题，如：

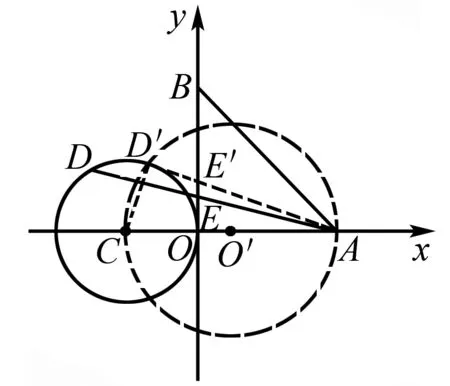
图2

例2如图2，点A(2,0),B(0,2)，圆C是半径为1，圆心坐标(-1，0)的圆.D是圆C上的动点，线段DA与y轴的交点是E，求△ABE面积最小值.

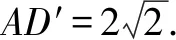
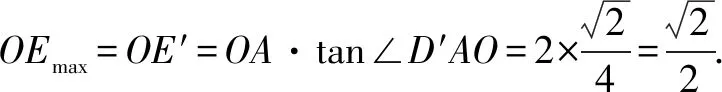
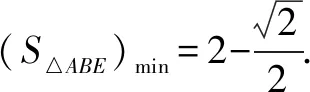
反思此题关键在于能够用恰当的式子合适表示S△ABE，并借助题意构建以线段AC为直径的辅助圆.

三、利用动点与定线段构成张角是定值，构建辅助圆

在同一个平面内，一动点C是已知直线AB外的一个点，且∠ACB为一定值，那么点C在以线段AB为弦长的某圆弧上；当∠ACB=90°特殊角时，点C在以AB为直径的圆上.熟悉此类动点与定线段所构成的角为定值的情形，明确此动点是在以定长线段为弦的圆上运动，特别是出现90°时，要高度留意90°的圆周角对应的那条弦实际就是直径的的特殊情况，是解决以此模型为基础的动点构成的最值问题.

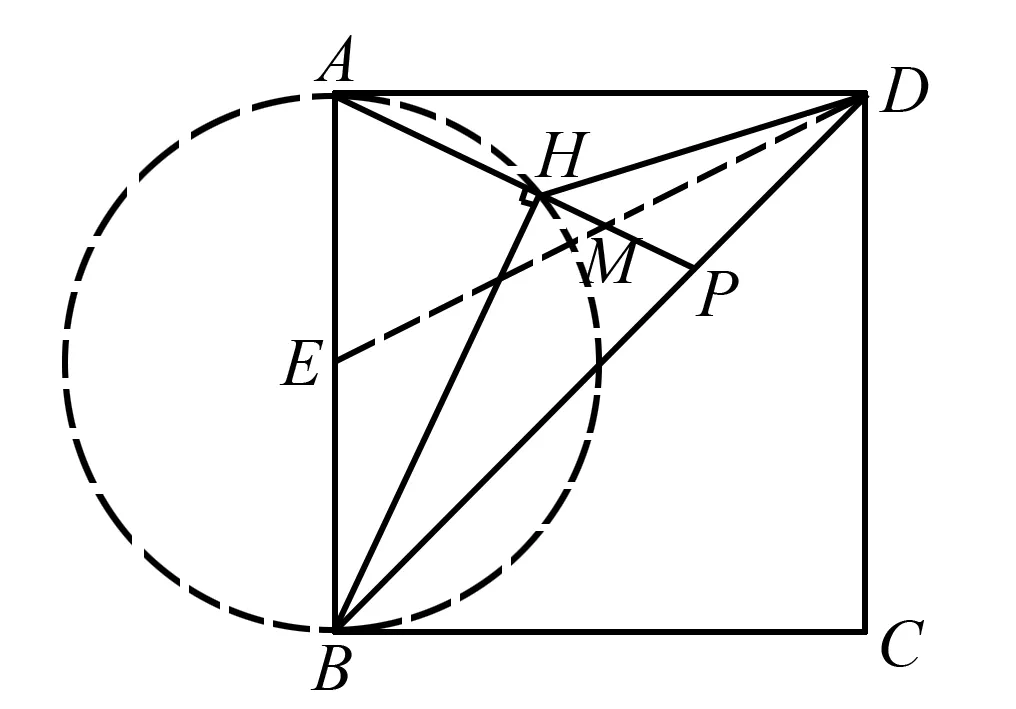
图3

例3如图3，边长是4的正方形ABCD对角线是BD，一异于端点B,D的点P在BD上运动，连接AP，并过点B作垂直于AP的垂线，垂足记为H，连接DH，则线段DH的位于( )时(位置)取值最小，最小值是( ).

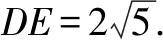
反思此题模型关键在于找出定角、以及定角相对相应的定线段；模型的运用离不开学生们已有的模型认识，也离不开需要充分挖掘题目隐含的信息，借助挖掘的条件快速锁定合适模型，然后依托模型的内容帮助学生们快速解题.因此，积累特定情况所对应的特殊模型结构是十分有必要的.

几何中最值问题，不仅要重视常见的几何法、代数法等基础方法，也要重视将“直”化“曲”，重视圆的知识的运用，熟悉常见的构圆情景，把握情景中的本质，通过构建合适的辅助圆，促进问题的转化与解决.