由一道简单物理试题引发的教学思考
何鹏 张子艳
(南宁市第三中学 广西 南宁 530021)
高一是学生整个高中学习的关键起始阶段,在物理学习中,高一阶段运动学与动力学的学习无疑是学生打开整个高中物理学知识大门的初始密码.在笔者实际的教学中能够明显地感觉到有部分学生在高中学习的开始阶段就存在着学习兴趣不高,上课注意力不集中,反映到对物理试题的解答上无法下笔的现象.从而造成考试分数不高,学生失去对物理学习的兴趣,导致不良循环.
本文从一个具体的物理题目出发,浅析在学生知识点解答和巩固的过程中需要完善的教学手段和需要达到的教学效果.
1 “拨云见日”从实际问题出发
在学习人教版高一必修1第四章“牛顿运动定律”后会遇到如下的一个基本试题.
【题目】如图1所示,在竖直平面内有一半圆,其直径水平且与另一圆的底部相切于O点,O点恰好是下半圆的圆心,现在有3条光滑轨道AB,CD,EF,它们的上下端分别位于上下两圆的圆周上,3条轨道都经过切点O,轨道与竖直线的夹角关系为α>β>θ,现在让一物块先后从3轨道顶端由静止下滑至底端,则物块在每一条倾斜轨道上滑动时所经历的时间关系为( )
A.tAB>tCD>tEF
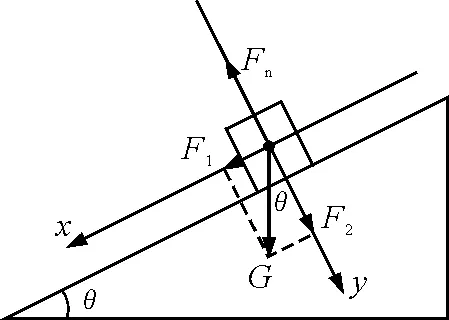
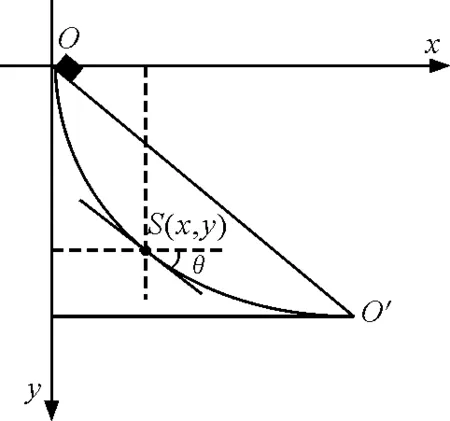
B.tAB C.tAB=tCD=tEF D.tAB=tCD 图1 题图 本试题是对“力的分解”“运动学公式”“牛顿运动定律”的简单综合运用.具体地,题中物块在3条轨道上下滑的情况,就是对物体在光滑斜面上下滑最简单的情境套用.在教学过程中可以将最基本的物理情境抽象出来,结合已经学习过的知识首先发散地回答如下问题:如图2所示,将物体放置在光滑斜面上,物体为什么下滑? 图2 基本物理情境 物体放在光滑的斜面上下滑,从静止到沿斜面向下运动,运动状态发生了改变,从牛顿第一定律可知是有力迫使它下滑.强调这一点,能让高一学生在思考中避免直觉认识所造成的误区,加深对力是使物体运动状态发生改变的原因,而不是维持物体运动的原因的理解. 接着对物体进行受力分析,如图3所示,物体只受重力和垂直于斜面的支持力作用.建立适当的直角坐标系,将重力在合适的方向上分解为使物体沿斜面下滑的力F1=Gsinθ和使物体紧压斜面的力F2=Gcosθ.由牛顿第三定律可知使物体紧压斜面的力F2(对斜面而言即对斜面的压力)与垂直斜面方向对物体的支持力等大、反向,垂直斜面方向上受力平衡.在沿斜面方向,因斜面光滑,无摩擦力,受力不平衡且分力F1沿斜面向下,所以物体要向下滑动.如果斜面有摩擦且最大静摩擦力足以克服重力的分力,此时物体会因为具有惯性,而且受力平衡,保持初始的状态静止在斜面上.而由牛顿第二定律,物体所受作用力与加速度的关系可知,在倾斜角为θ的光滑斜面上物体下滑的加速度a=gsinθ. 图3 对斜面上的物体受力分析 具体到图1的问题,在以上既定知识的基础上结合运动学公式分析.可以设上面圆的半径为R,下面圆的半径为r.分析轨道EF上的情况,轨道EF长度为l=2Rcosθ+r,对物块受力分析可知物块沿EF下滑的加速度a=gcosθ,运动时间 轨道与竖直方向的夹角越小,时间越短,根据α>β>θ判断tAB>tCD>tEF,对照选项A对. 对于此部分浅显的物理知识,应陈述指导式教学,通过复习巩固使学生加深对基本物理知识的印象.而其中经典而重要的物理原理则应着重强调,教师可以采用先提问后师生回答的正向记忆加强手段,在明晰抽象原理的同时可以列举相关实例进行说明,这样有助于学生理解性记忆.从物理学基本原理出发,在具体问题中反复“玩味”,可以很好地培养学生的科学思想,摒弃“想当然”“应该是”的问题思想.对此如若不加以引导改正,势必对以后的学习会有很大的阻碍作用.一方面,往往学生在试题解答中出现的错误归根到底是没有对物理学的基本原理有一个深刻的理解,从而导致理解错、用错.并且如果学生似懂非懂,会使学生在学习中产生可惜、郁闷的消极情绪.另一方面物理学是一门迷人的自然科学,之所以迷人是因为物理学的基本原理可以很好地描述总结自然界中的各种问题.在社会生活中利用物理学规律实现资源利用、社会利益的最大化.对物理学基本原理的把握能够实现学生精神层次的极大满足,增加学习物理的主观能动性,对学生学习效果产生极大的正面作用. 教学应具有启发性,在涉及此问题中可以对学生思维能力进行启发式锻炼.让学生多疑问、多思考、多条路解答问题. 通过不同解决问题的方法对思维进行扩展在物理学习中显得尤为重要,可以使学生多方面地思考问题,从而又快又准地解决问题.对特殊问题的特殊解法的思考,可以培养学生推陈出新,挑战已有不利框架的科学态度.对未知知识探索是学生的本能行为,只要有足够的原动力一定会有事半功倍的效果.因而要在后期的学习中针对一类问题延伸扩展,加宽学生的认知广度,如对于此试题还有如下难点可以用来探究. 问题一:如图4所示,若斜面光滑但物体下滑的轨迹不同(直线、摆线、圆弧等),物体从O运动到O′沿哪条路径下滑时间最短?也就是赫赫有名的最速下降曲线问题(摆线问题)[1].历史上许多名人如牛顿、莱布尼兹以及Jakob Bernoulli等人都对此问题研究过,但最终由Leonhard Euler提出了曲线极值问题的微分方程并建立变分法,使得此问题得到圆满解决[2,3]. 图4 最速下降曲线问题图示 最速下降曲线问题的实质是求解泛函极值问题,可以利用变分法求解此类问题.如图4所示,质点从O点滑到O′点,并选取坐标系.设物体运动的曲线轨迹方程为y=y(x),已知物体的质量为m,重力加速度为g,物体的速度为v(t),其中t为物体的下滑时间.根据能量守恒定律可得,在下滑过程中的任意位置S(x,y)都满足公式 进一步可以得到对应的速度 设质点下滑路程为s(t),则速度的微分形式为 即 因此物体整个过程运动的时间为 由变分法可知极值曲线轨迹满足欧拉方程 因此方程的解为 y(1+y′2)=c 初始条件满足y(0)=0,可得 已知,当摆角很小时,单摆的周期公式近似为[5] 其中l为摆线的长度,从公式中我们可以知道单摆的周期只与摆线的长度和当地的重力加速度有关.当摆线长度不变,重力加速度不变时,单摆具有等时性.已知最速下降曲线是一条摆线,那么在最速下降曲线上任意位置释放的物体,从高处下滑后均会在同一时刻到达最低点. 问题二:在如图5所示的斜面上小物块沿不同路径(直线、凹曲线、凸曲线等)下滑,如果斜面不光滑且不同路径上小物块的动摩擦因数μ相同时,小物块通过不同路径到达斜面底部的速率如何?如果斜面光滑,小物块通过不同路径到达斜面底部的速率又如何? 图5 斜面上的小物块沿不同路径下滑 在斜面光滑没有摩擦的影响时只有重力做功,与路径无关,小物块滑到斜面底部时速率相同.而对于有摩擦时的情形,计算中需要涉及少量的微积分知识则相对复杂一些.如对于凸面,摩擦力的方向沿切线反方向,大小为μmgcosθ,其中θ为在该点切线与水平方向的夹角,元位移沿切线方向,大小为ds.则有 其中dl为水平方向的元位移,积分得到的表达式为μmgL.因而动摩擦因数μ相同,滑到斜面底部时速率也相同.此题的解析建立需要一定的数学基础,但学生应能较清楚地明白此题的物理思想.其中涉及到“保守力、耗散力做功”“功能关系”等重要知识点,只需点拨学生对此结论有感性的认识,摈弃用非科学的思想去考虑问题. 针对以上扩展内容,因为部分涉及了较复杂的大学物理和高等数学的内容,对学有余力的学生,也仅限于感性的了解而不要求掌握.从简单模型出发,在解决已有问题的基础上对已有问题的扩展和升华是提高学生求知欲和学习积极性的重要手段.但在扩展时一定要把握好度,防止学生因知识体系超纲,发散过深如坠云里雾里,反而事倍功半. 物理教学是一门需要时刻操练的艺术.正所谓“万事开头难”,深入物理学习的起始阶段显得尤为关键,通过启发式引导,针对不同学情层次的高中学生,通过“反复式思考”教学,多提问、多深化、多升华,从而全面提高学生学习的兴趣.通过适当的“扩展式”教学,将书本上的知识利用到实践中,将理论转化为实践,对锻炼学生思维、培养学生解决问题的能力和全面提高学生物理内涵起到积极的推动作用.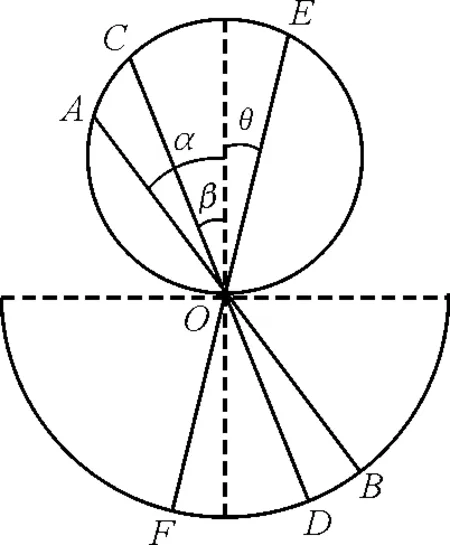

2 注重对物理学基本原理的理解与把握
3 思维与知识扩展

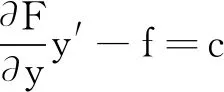




4 结束语

