余弦激励的Rossler超混沌系统动力学分析及电路实现

方 淼，方 帆

1.安徽大学江淮学院理工部,安徽合肥,230039；2.巢湖学院教务处,安徽巢湖,238000

自1990年，Pecora等发现了混沌可以被同步，并且用电路对混沌同步进行实现[1]后，混沌被用于保密通信成为信息安全领域研究的热点。其中超混沌系统由于具有多个正的Lyapunov指数，动力学行为更加难以预测[2]，能为保密通信提供更高的安全性。因此许多研究人员在构造新的超混沌系统方面进行了深入的研究，提出了一系列超混沌系统。Li等在Chen 系统的基础上提出了超混沌Chen系统[3]；方淼将忆阻器引入Lü系统，构建了一个四维超混沌系统，并采用等效电路对系统进行了实现[4]；阮静雅等将二次型磁控忆阻器作为系统的正反馈项设计了Lorenz超混沌系统并进行了电路实现[5]；乔晓华等将忆阻元件引入Lü系统构造了一种具有隐藏动力学特性的忆阻超混沌Lü系统[6]。这些超混沌系统往往通过在已有的典型三阶混沌系统中引入非线性控制器来实现超混沌，电路结构较复杂且实现有一定的难度。

文献[7]提出通过给Chen系统施加正弦信号产生超混沌的方法，但施加的正弦信号要达到一定的频率才能进入超混沌状态。受此启发，本文首先通过给经典Rossler系统施加余弦激励的方法，构建了一种新颖的、改进型的Rossler超混沌系统，然后采用基本动力学方法对系统的特性进行了研究，当余弦激励信号的频率达到一定值后，该系统处于恒定超混沌状态。最后采用模拟器件设计并实现了相应的电路，电路仿真的结果和数值仿真结论一致，验证了该超混沌系统的可行性。

1 Rossler混沌系统

Rossler混沌系统可用常微分方程表示[8]为:

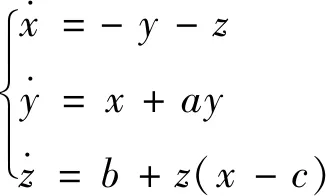
(1)

式中，x，y，z为3个状态变量，a、b、c为Rossler系统的控制参数。当a=0.2，b=0.2，c=5.7时，系统处于混沌状态，设置初始条件为(1,1,1)时，系统生成一个单涡卷折叠混沌吸引子如图1所示。

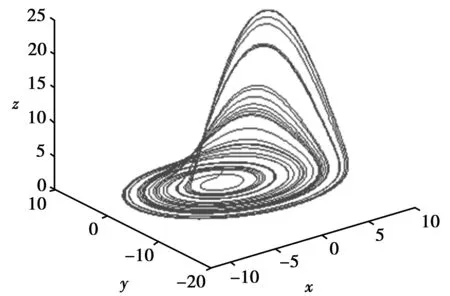
图1 Rossler混沌系统的混沌吸引子

2 余弦激励的Rossler系统

在Rossler混沌系统的第二个方程中添加余弦信号γcoswt作为激励信号，激励信号受参数a控制，其振幅为γ，角频率为w，即可构建出一种新的超混沌Rossler系统，其数学模型表示为：

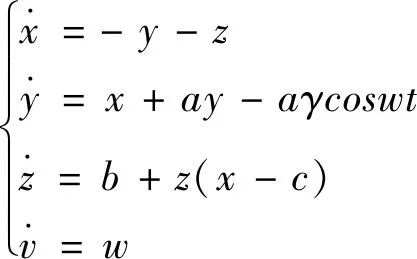
(2)

式中，x、y、z、w为状态变量，a、b、c为经典Rossler系统的控制参数，保持这些参数的数值不变，选择余弦激励信号的角频率w作为系统唯一的可调节参数。

当γ=0.6，w=10时，设置系统的初始条件为(1,1,1,1)，系统(2)产生的混沌吸引子如图2所示。利用Wolf方法计算系统的Lyapunov指数可得LE1=0.057，LE2=0.015，LE3=0，LE4=-5.405，此时系统的Lyapunov维数为：

(3)

系统(2)有两个Lyapunov指数大于0，且其Lyapunov维数为分数值，显然该系统表现出了超混沌特性。

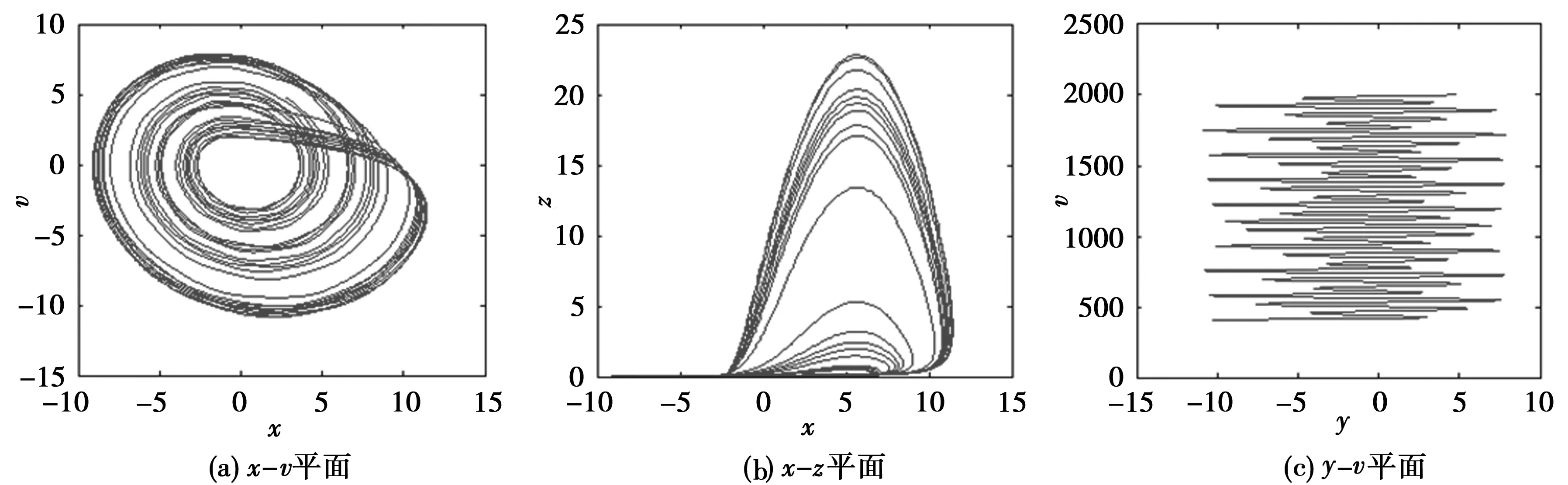
图2 超混沌吸引子相图

3 系统动力学分析

3.1 平衡点的稳定性

(4)

相应的特征方程为：

P(λ)=det(λE-JE)

(5)

计算可得其特征值为：

λ1，2=±5.14i，λ3=0.1922，λ4=0

λ1,2是一对共轭虚数，λ3为正实数。根据Routh-Hurwitz条件[9]可知平衡点E1为不稳定结点。在平衡点E2附近线性化系统(2)，可得系统的Jacobian矩阵为：

(6)

计算可得其特征值为：

λ1，2=0.096±0.995i，λ3=-5.085，λ4=0λ1,2是一对具有正实部的共轭复数，λ3为负实数，可知平衡点E2为不稳定的鞍焦点。

3.2 Lyapunov指数谱和分岔图

为了研究新引入的状态变量的参数变化对系统(2)的动力学行为的影响，固定参数a=0.2，b=0.2，c=5.7，设置系统初值为(1,1,1,1)，当γ=0.6时，取系统参数w∈[0, 15]，步长为0.01，系统的Lyapunov指数谱如图3所示。与之对应的状态变量y的分岔图如图4所示。

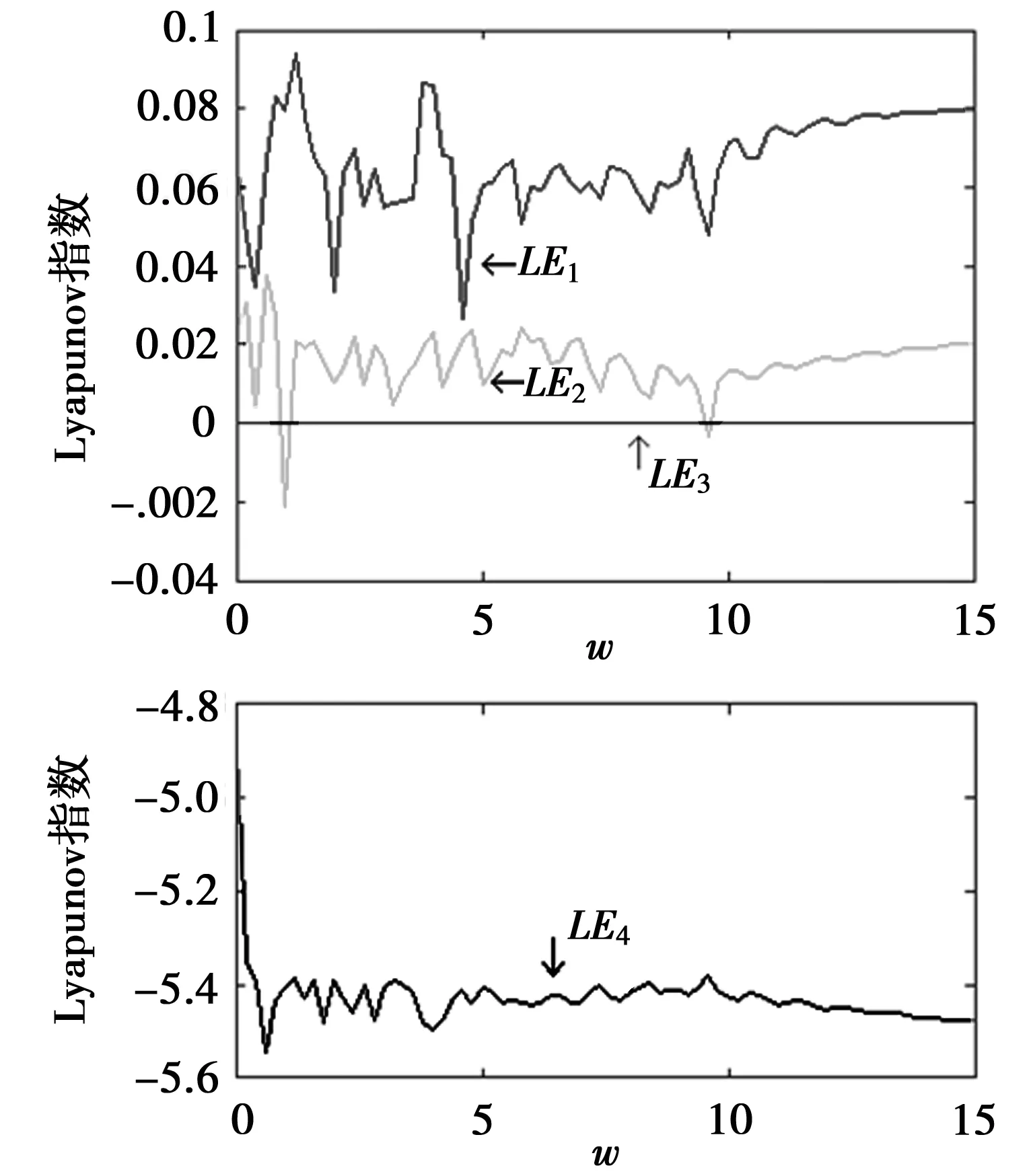
图3 系统随参数w变化的Lyapunov指数谱

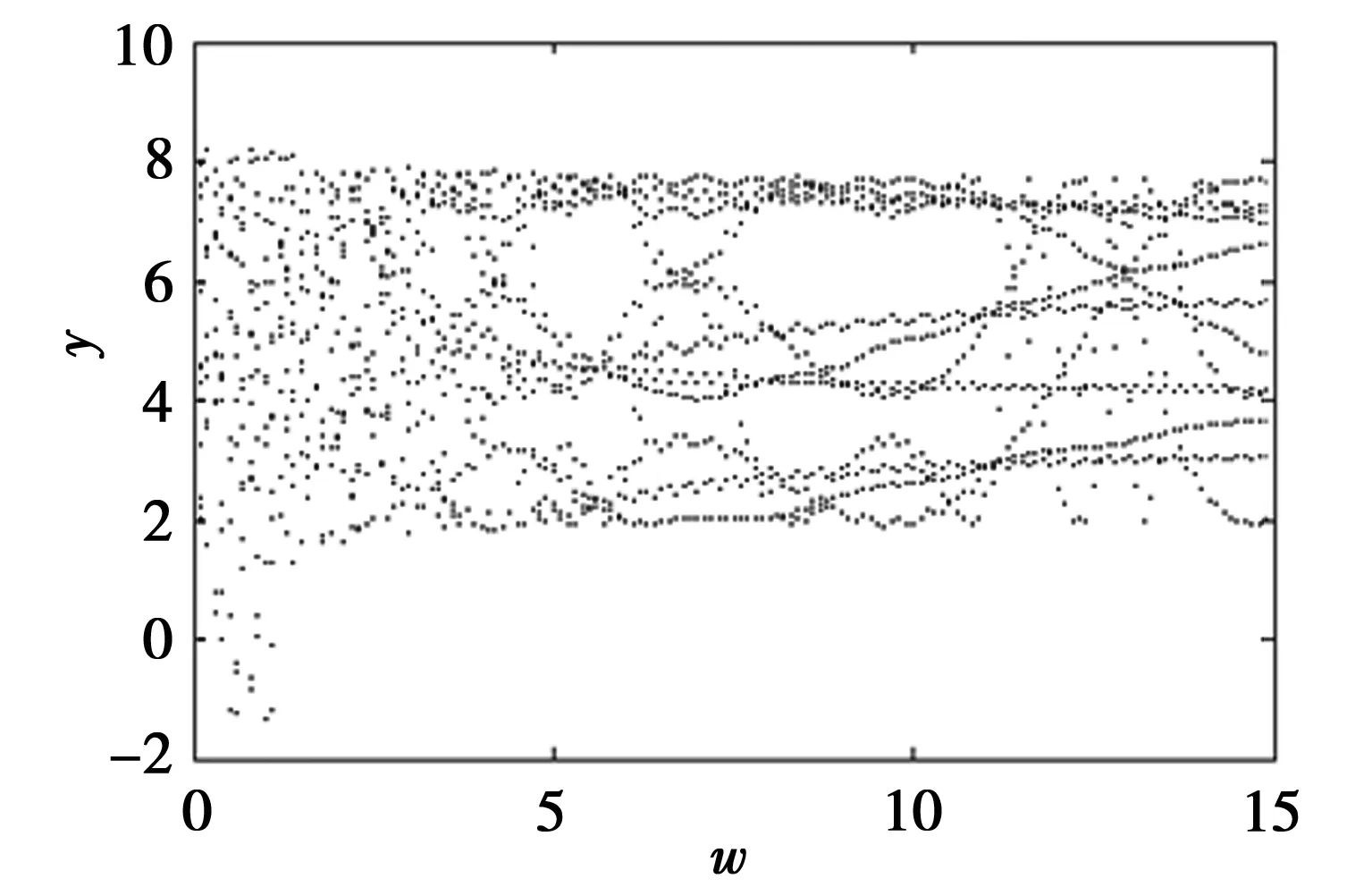
图4 状态变量y随参数w变化的分岔图

由图3、图4可知，当参数w在[0，15]区域内变化时，除了w=1和9.6时，LE2从正数变为负数，此时LE1>0，LE3=0，LE4<0，Rossler系统仅有一个正的Lyapunov指数，系统处于混沌态，在其他区域内LE1、LE2始终大于0，即Rossler系统始终处于超混沌状态。且当w增大到13后，LE1、LE2基本保持不变，即系统处于恒定的超混沌状态，与其他忆阻超混沌系统相比，该系统不因控制参数w的扰动或微小变化而导致状态发生变化，其结构稳定，具有强鲁棒性[10]，适于作为随机信号源。

3.3 Poincaré截面

通过选取合适的Poincaré截面，可将系统随时间的连续运动转换为Poincaré截面上的一个离散映射[5]，降低系统的维数,同时保持原系统的拓扑性质，便于对多变量的系统的混沌行为进行判断。因此选取w=10，对系统作Poincaré截面分析。系统在x=-2截面上Poincaré映射如图5所示，是典型的分型结构，进一步说明了该系统的超混沌特性。

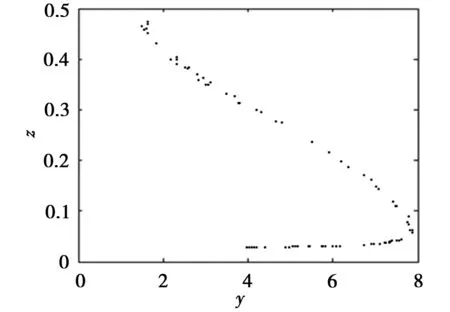
图5 系统在x=-2截面上的Poincaré映射

4 电路实现

连续混沌系统可采用电阻、电容、运算放大器和模拟乘法器等分立元器件进行电路实现。本文提出的余弦激励的Rossler超混沌系统，选用AD633模拟乘法器和LM741运放作为主要器件来搭建模拟电路。由于模拟乘法器的容许电压范围为±10V，运放的容许电压范围为±15 V。为确保实际电路的信号幅度在合适的动态范围内，不因过小而导致信号失真，因此在不改变系统性能的条件下需对系统状态变量进行线性缩放。根据之前的数值仿真结果可知，超混沌吸引子的状态变量x，y，z，v分别在-10～15，-15～10，0～25,0～2500范围内变化。因此对系统(2)的状态变量进行线性缩放如下：

(x,y,z,v)→(2x,2y,2z,v)

(7)

变换后系统(2)对应的电路方程为：

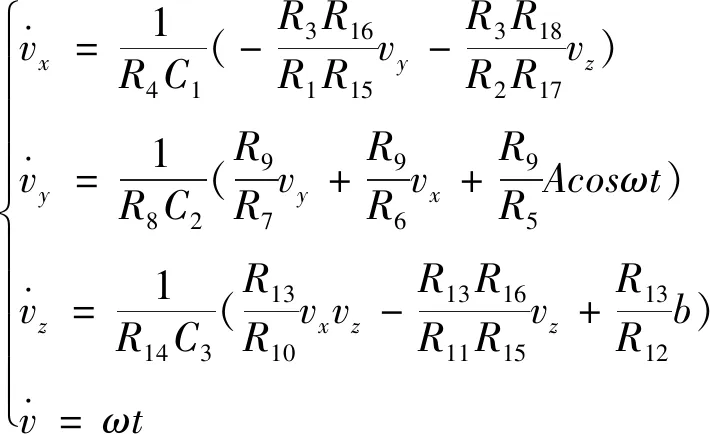
(8)

基于式(8)的电路状态方程，可设计并实现电路原理图如图6所示。

图6 超混沌系统的电路图

选择时间尺度因子τ=1/(RC)中的R=10 kΩ,C=1μF。与系统(2)比较，可得图6中各元器件的参数分别为：

R7=50 kΩ

R1=R2=R6=10 kΩ

R3=R9=R13=100 Ω

R4=R8=R14=R12=R15=R16=R17

=R18=10 kΩ

R5=20 kΩ，R10=5 kΩ

C1=C2=C3=C=1 μF

A=0.6R11=1.8 kΩ

b=0.1

采用PSPICE对上述电路方程进行电路仿真，仿真结果如图7所示。电路仿真结果和数值仿真结果基本一致，再次验证了该超混沌电路的正确性。

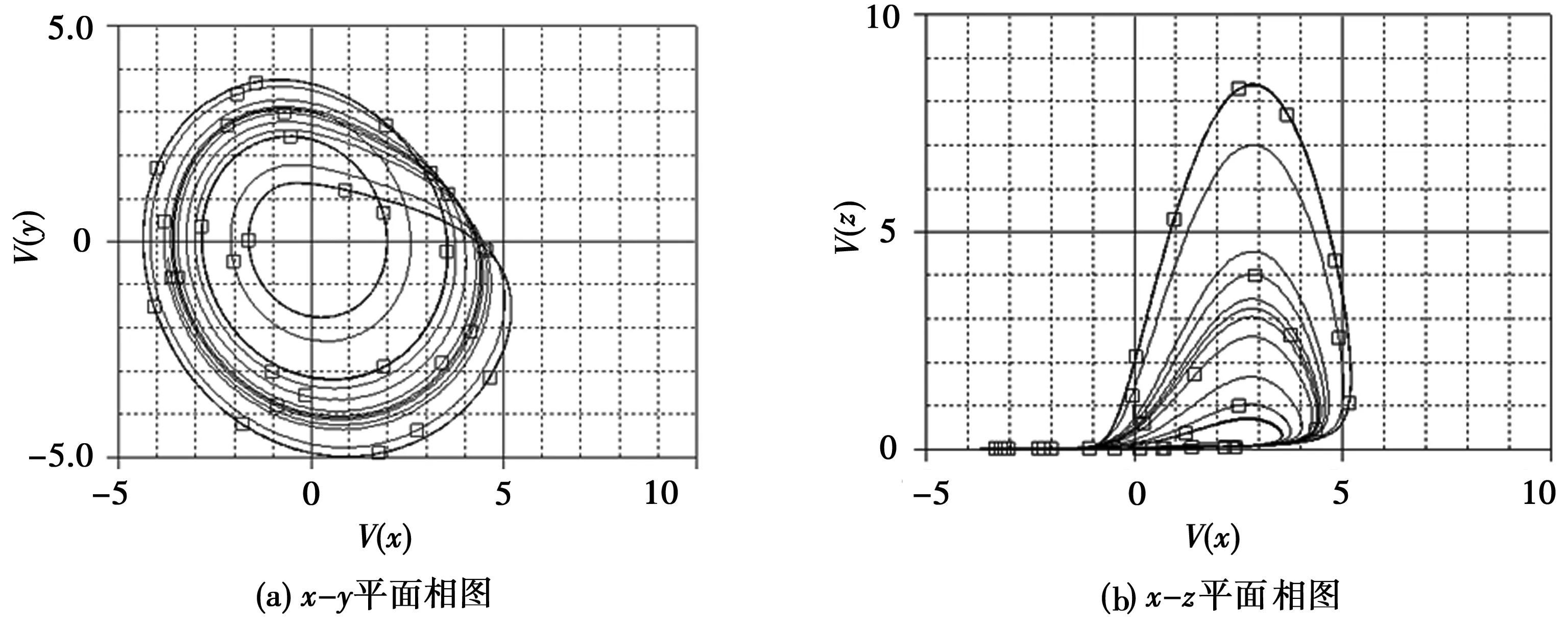
图7 超混沌系统的电路仿真图

5 结论

本文通过对经典Rossler混沌系统施加余弦激励的方法，构建了一种新颖的、改进型的Rossler混沌系统，该系统出现了恒定的超混沌特性。通过对系统的分岔图、Poincare截面、Lyappunov指数谱等动力学特性进行分析，验证了系统的超混沌特性。为了进一步验证系统的动力学行为，采用通用的运算放大器和模拟乘法器实现了系统的模拟等效电路，并对该等效电路通过PSPICE进行了电路仿真，仿真结果和数值仿真以及理论仿真结果一致，验证了电路的有效性和可实现性，为超混沌电路的同步控制应用提供了理论基础。