空间插值法在土壤养分测定中的比较研究

潘正高，赵晋陵

1.宿州学院安徽省农业生态大数据工程实验室宿州实验室，安徽宿州,234000；2.安徽大学农业生态大数据分析与应用技术国家工程研究中心，安徽合肥，230601

土壤养分是土壤提供植物生长所必需的营养元素[1-3]。了解土壤养分的空间分布是开展土壤试验和配方施肥，开展精准农业的基础。缓效钾是存在于土壤层状硅酸盐矿物层间的一些钾离子，属于非交换性钾，是土壤有效钾的一部分。土壤中的缓效钾是速效钾的储备，当土壤中速效钾由于作物吸收而减少时，缓效钾就会释放出来以补充速效钾的缺失[4]。由于土壤养分分布的复杂性和样本数据的局限性，依靠传统的现场测量难以了解整个研究区域的养分分布情况。空间插值技术可以从离散的地面真实数据中得到空间分布趋势，极大地促进了大规模评价土壤养分的工作[5]。

空间插值分析是地理信息系统(GIS,Geographic Information System) 中常用的空间分析方法，也是GIS系统区别于其他信息系统的重要特征之一[6-7]。空间位置距离已知观测点越近，特征值越接近；空间位置距离已知观测点越远，其特征值越不可能相似。这是空间插值技术最基本的理论假设[8]。在这一理论假设的基础上，学者们提出了反距离加权插值、克里金插值、样条函数插值、趋势曲面插值等多种插值方法。

一般情况下，研究者需要根据样本数据的分布特点选择不同的插值方法。本文以土壤养分中的缓效钾(SAK，Slowly Available Potassium)为研究对象， 对不同插值分析方法的有效性进行比较研究，以期找出土壤中SAK的最优插值方法。

1 材料和方法

1.1 收集和预处理土壤养分数据

本文收集了宿州市埇桥区农村麦田土壤养分数据。采用网格单点采样方法，利用亚米高分辨率GPS接收机对采样点进行精确定位，共收集178个样本点。利用GIS软件ArcGIS[9]将GPS测得的采样点记录坐标转换为空间坐标的空间点，并进行投影变换，生成含有缓效钾养分含量信息的样本分布。

1.2 反距离加权(IDW,Inverse Distance Weighted)

反距离加权(IDW)插值法是使用一组采样点的权值的线性组合来确定像素点的值[10]。权值是一个逆距离函数，其函数表达式如式(1)(2)所示。

(1)

(2)

其中，ve是与采样点(xi,yi)相关的变量值，λi是权重系数，p是指数值，di0是预测点s0与已知样点si之间的距离。样点在预测点值的计算过程中所占权重的大小受参数p的影响，也就是说，随着采样点与预测值之间距离的增加，标准样点对预测点影响的权重按指数规律减少。在预测过程中，各样点值对预测点值作用的权重大小是成正比例的，这些权重值的总和为1。通过计算均方根的最小误差，可以求出最佳值。因此，需要插值的曲面是具有局部因变量的曲面。该方法假定，映射变量的减小是由于受到样本位置之间距离的影响。该方法所有的样本点都参与未知点的Z值估计，适合样本数据集均匀分布情况，是一种全局插值方法。它是一种精确的插值方法，即插值生成的曲面上的预测样本点值与实测样本点值完全相等。

1.3 普通克里金(OK，Ordinary Kriging)

克里金法是一种高级统计方法，通过一组Z值的离散点生成估计曲面[11]。不同于其他插值方法，克里金法采用产生输出曲面的最佳估计方法，对Z值表示现象的空间行为进行综合研究。它假设采样点之间的距离或方向能够反映出空间相关性，进而用来说明表面变化。克里金法可以通过数学函数拟合指定数量的样本点或者指定半径范围内的样本点，以确定每个位置的输出值，常用样本点的数据加权和表示，如式(3)所示。

(3)

其中Z(si)为位置i的实测值，λi为位置i的未知权重，s0为未测量位置，N是测量指标。权重不仅由测点之间的距离决定，还由预测位置决定；它还取决于基于测量点的整体空间布局。该方法常用于土壤科学和地质学中。

1.4 样条函数(Spline，Spline Function)

样条函数插值分析法是采用数学函数来估计值，这些函数最小化了整个曲面的曲率，从而生成刚好通过输入点的平滑曲面[12]。

样条函数有两种方法：正则样条函数和张力样条函数。正则样条函数方法使用可能超出示例数据范围的值来创建一个渐进光滑的表面。张力样条函数法根据建模现象的特点控制表面硬度。它使用样本数据范围内更严格约束的值创建一个不太平滑的表面，曲面插值公式如式(4)。

(4)

其中,N是点的数量，λj是通过求解一个线性方程组得到的系数，rj是点(x,y)到点j的距离。根据所选取的选项，T(x,y)和R(x,y)是不同的。

对于正则化选项，T(x,y)和R(x,y)如方程式(5)和(6)所示。

T(x,y)=a1+a2x+a3y

(5)

(6)

其中，r表示点到样本之间的距离，τ2是权重参数，K0是修正贝塞尔函数，c是常数0.577215。权重参数τ2确定了在最小化过程中依附于三阶导数项的权重，增大权重参数可以获得更平滑的曲面，一般取0到0.5之间的值，使用正则化选项可以确保曲面光滑和一阶导数曲面光滑。该方法主要用于计算插值曲面的二阶导数的情况。

对于张力选项，T(x,y)和R(x,y)如式(7)和(8)所示。

T(x,y)=a1

(7)

(8)

其中，r是点到样本的距离，φ2是权重参数，K0是修正贝塞尔函数，c表示常数0.577215。权重参数确定了在最小化过程中依附于一阶导数项的权重，当权值为零时，它就是基准的板样条函数插值方法。

1.5 趋势插值(Trend Interpolation)

趋势插值是一种全局多项式插值方法，它能拟合由多项式函数和输入采样点定义的光滑曲面[13]。趋势面将逐渐变化，并在数据中捕获粗尺度模型。模型函数如式(9)所示。

(9)

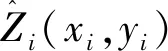
1.6 插值结果检验

在生成最终曲面之前，我们需要知道模型在预测未知位置的值的精度。本文采用交叉验证的方法来测定模型的质量[14-16]。目标模型的平均误差(ME)应该接近于0，且具有较小的均方根误差(RMSE)。本文以RMSE作为评价四种插值方法的指标，其公式如式(10)所示。

(10)

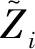
2 空间插值的结果和分析

2.1 插值结果比较

2.1.1 克里金插值模型的比较

普通克里金插值是应用最广泛的克里金插值，它包括许多半方差函数类型。本文选取球面函数、指数函数和高斯函数三种模型进行插值。三种模型的预测误差如表1所示。由表可知，指数函数模型的RMSE最小，插值效果最好。

表1 普通克里金插值模型的比较

2.1.2 样条函数插值模型的比较

采用正则样条函数法和张力样条函数法进行样条插值，预测误差如表2所示。对比两种插值方法的均方根误差，张力样条的RMSE最小。因此，张力样条函数的插值方法更为合适。

表2 样条插值模型的比较

2.2 插补精度分析

本文选择RMSE作为插补精度的比较指标。我们知道，绝对值越接近，均方根误差就越小。表3为各种插补方法的交叉验证结果。由表可知，克里金插值法的均方根误差最小，其中指数函数法插值法最优。

表3 各种插补方法的交叉验证结果

3 结 语

采用不同插值方法对宿州市埇桥区土壤养分中缓效钾的插值结果进行了比较，普通克里金法插值精度高于其他三种插值方法。因此，考虑到插补精度和计算过程的复杂性，普通克里金法是缓效钾插补的最佳选择。插值方法的选择是数据类型和计算效率之间的平衡，任何方法都不是绝对唯一的。由于采样点的密度、现场数据的取值或变化范围、地面液体的复杂程度等因素的影响，不同插值产生的结果可能会有较大的差异。本文只选取了四种插值方法进行比较，其他插值方法的选择还需要进一步研究。