一种基于中国剩余定理的高效乘法器设计
崔馨园 李银 袁华强
(东莞理工学院 计算机科学与技术学院,广东东莞 523808)
有限域GF(2m)算术运算在椭圆曲线密码系统(ECC)、编码理论和密码学中具有重要应用价值[1]。有限域算术运算中包含了加、减、乘、除、幂和求逆等多种运算,其中幂运算和求逆运算又可将其转化为乘法运算,由此可见乘法运算是有限域算术运算中最常用的运算方式之一[2-4]。在计算机技术发展日新月异的今天,计算机需要处理的数据呈指数增长,人们对计算机运算速度的要求也逐渐提高。若能优化乘法器的结构,降低有限域乘法算法的开销,并均衡算法的时间复杂度和空间复杂度,对提高有限域乘法运算的运算速度至关重要。因此,设计高效的有限域乘法算法对有限域算术运算的广泛应用以及对提高密码学领域的实用性能都具有重要意义。
有限域乘法器按每个时刻处理的比特数不同而分成:比特并行乘法器、比特串行乘法器和数字并行乘法器,其中比特并行乘法器在研究乘法器优化领域上应用范围最广[5]。根据乘法器的空间复杂度,比特并行乘法器分为三种类型,分别是平方级比特并行乘法器(Quadratic Bit-Parallel Multiplier)、亚平方级比特并行乘法器(Subquadratic Bit-Parallel Multiplier)和混合型比特并行乘法器(Hybrid Bit-Parallel Multiplier)。平方级比特并行乘法器时间复杂度最低,亚平方级比特并行乘法器空间复杂度最低,而混合型比特并行乘法器可以在时间和空间复杂度之间进行权衡[3]。有限域乘法器若按有限域基的表示方式又可分为:多项式基、正规基、对偶基等[6]。若采用多项式基表示方式,则有限域的算术运算也是对应多项式的运算,那么有限域乘法可以分成以下两个步骤:1)两个多项式相乘,2)步骤1)的结果对不可约多项式f(x)取模[7]。其中,步骤2)的复杂程度由多项式f(x)的类型选择不同来决定,最常使用的不可约多项式为三项式和五项式。本文采用多项式基表示方式,选取的f(x)类型为不可约五项式,对混合型比特并行乘法器进行优化设计。
多项式基混合乘法器通常在多项式乘法部分采用分治算法。Karatsuba算法(KA)是最常用的分治算法,与最快的平方级乘法器相比,这些基于KA的混合乘法器通常需要至少一个TX,其中TX是一个2输入XOR门的延迟。除KA外,其他著名的分治算法,如Winograd短卷积算法和中国剩余定理(CRT),也广泛应用于开发并行乘法器。
2015年Fan首次将中国剩余定理(CRT)运用到乘法器的设计[3],提出了一种新的有限域乘法运算方法。他在步骤1)采用了传统的方法,步骤2)没有采用经典的KA算法,而是创新性的提出了使用中国剩余定理(CRT)计算。Fan的架构可以为某些特定m阶范围内的不可约三项式找到最快的比特并行乘法器,使其具有与最快的比特并行乘法器相同的时间复杂度,并能降低它们的空间复杂度。2017年Zhang和Fan进一步优化了该结果[7]。笔者研究Fan研究结果发现,基于中国剩余定理(CRT)的乘法器关键思想在于:将步骤2)模约简转换为对f(x)的非常数部分取模求得的商和余数的计算。但文献[8]和文献[9]的乘法器仅适用于部分不可约三项式,对范围更广的不可约五项式并不适用。为扩大基于CRT的乘法器算法适用范围,2021年Li与笔者选择为部分不可约五项式设计基于CRT的更高效的混合型比特并行乘法器[10],结果表明,除了不可约三项式外,其他特殊的多项式也能具有适合应用CRT和开发高效混合乘法器的适当结构。在此过程中,发现若能设计一个通用的公式,对满足优化条件的f(x)都能采用此通用公式来设计与其对应的CRT乘法器,那么将使基于CRT的乘法器构造更一般化。这为本文研究提供了方向,也是本文提出的乘法器模型的理论基础。
1 相关工作
1.1 中国剩余定理(CRT)
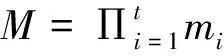
(1)

1.2 相关引理
定义1设a=anxn+an-1xn-1+…+a1x+a0,a属于有限域F2[x],则a的反转定义为revk(a)=xka(1/x)。当k=n时,rev(a)表示的是将a系数反转后的多项式:
rev(a)=revn(a)=a0xn+a1xn-1+…+an-1x+an.
引理1[12]设a、b是有限域F2[x]上的多项式,次数分别为n,l且(n>l)。q、r分别为a除以b得到的商和余数,则:
revn-l(q)≡revn(a)revl(b)-1modxn-l+1
结合引理1可以得出求商Q的通用公式:
Q=revn-l(revn-l(Q)),R=a-Qb.
(2)
2 乘法器实现
笔者在乘法器的设计环节未采用文献[8]和文献[9]的方法,而是设计了一个通用公式来搭建基于CRT的混合乘法器模型。下面将对通用公式进行说明。
设f(x)是环F2[x]上的不可约多项式,A、B是多项式基上任意两个多项式,且A,B∈GF(2m), 将A,B的有限域乘法记为:ABmodf(x)。另设F(x)=L1f(x)+L2,其中L1、L2∈F2[x],degree(L1)=l1、degree(L1)=l2。通用公式的设计思想关键是不直接计算ABmodf(x),而先计算更容易求得的AB关于F(x)的商Q和余数R,然后通过巧妙的转化可以求得ABmodf(x)的结果,如下所示:
A·Bmodf(x)=Q·F(x)+Rmodf(x)=
(L1·f(x)+L2)Q+Rmodf(x)=
L2·Q+Rmodf(x),
(3)
如式(3)所示,A、B的有限域乘法运算被转换为关于f(x)的商Q和余数R的计算,再对f(x)进行模约简两个运算步骤,为了开发高效的CRT混合乘法器,应该选择能使上述计算更容易的L1和L2。因此,选择L1、L2时应满足以下条件:
a)Q和R容易计算;
b)L2应尽量简单;
c)对f(x)进行模约简的步骤容易计算。
很明显,在这三个条件中,条件a)依赖于F(x)的计算公式,而b)和c)主要依赖于f(x)的选取,由此更凸显了选取f(x)的重要性。
综合考虑以上要求,选择f(x)=xm+xm-k+xm-2k+x+1这种不可约的五项式,则L1=1、L2=x+1、F(x)=xm+xm-k+xm-2k。套用式(3),得出有限域乘法的计算公式为:ABmodf(x)=(x+1)Q+Rmodf(x),接着分别计算出Q和R,再对f(x)模约简即可求出A、B两个多项式的有限域乘法运算结果。
2.1 计算AB关于F(x)的商Q:
此时由于F(x)中包含的项数不确定,因此不能使用文献[8]中的Fan计算方法来计算商Q,所以选择使用文献[12]中引入的方法,该方法在1.2中介绍了核心引理,套用式(2)可以得到:
revm-l1-2(Q)=
rev2m-2(AB)·revm+l1(F)-1modxm-l1-1,
(4)
由于l1=0,revm+l1(F(x))=revm(F(x))=x2k+xk+1,使用扩展欧几里得算法易得模逆,该算法公式随m和k之间的大小关系变化而变化,最多包含四项。主要有以下几种情况:
revm(F(x))-1=xk+1 2k revm(F(x))-1=x3k+xk+1 3k+1 revm(F(x))-1=x4k+x3k+xk+1 4k+1 (5) 由式(4)不难看出,商的计算可以在2Tx延迟中实现。相反,如果m> 6k,revm+k(F(x))-1超过四项,会导致商的计算更复杂,因此只考虑2k revm-2(Q)=rev2m-2(AB)·(xk+1) modxm-1 2k revm-2(Q)=rev2m-2(AB)·(x3k+xk+1) modxm-1 3k+1 revm-2(Q)=rev2m-2(AB)·(x4k+x3k+xk+1) modxm-14k+1 (6) 3k+1 (7) 由于F(x)=xm+xm-k+xm-2k=xm-2k(x2k+xk+ 1),R的计算可以使用CRT算法来实现。首先,xm-2k和(x2k+xk+ 1)相关的贝祖等式(Bezout identities)根据m和k之间的大小关系变化而变化: (x2k+xk+1)·1+xm-2k·(x4k-m+x3k-m)=1 2k (x2k+xk+1)·(xk+1)+xm-2k·x5k-m=1 3k (x2k+xk+1)·(x3k+xk+1)+xm-2k·(x7k-m+x6k-m)=1 5k (8) 因此,余数R使用CRT算法计算过程如下: (9) 3k [AB]xm-2k·(x5k+x4k+1) modF(x)= (10) 不难看出,[A]x2k+xk+1和[B]x2k+xk+1可以在2Tx时延中并行实现,并能计算出[A]x2k+xk+1和[B]x2k+xk+1所需的XOR门数: (11) 将有限域乘法ABmodf(x)记为C, 则C=(x+1)Q+R。因此,C可以通过分别求出R、Q和xQ的结果并将它们相加得到。为了更有效地计算R,将R的计算公式划分成R1、R2两部分求解,可得: 3k (12) 4k (13) (14) 分别对设计的乘法器的时间复杂度和空间复杂度进行分析,并将其与主流的同类型乘法器进行比较,同时还介绍了整个乘法器模型构建的运算过程,从结果倒推可知,整个过程从A、B两个多项式的乘法开始,过程中包含大量对系数进行的异或运算以及加法运算,分析乘法器模型的时间和空间复杂度,需要从分析AND电路门和XOR电路门的数量和延时开始,其中对系数的计算和分析显得尤为重要。 先从3k 注意,表1所表示的ti在计算时先分别并行计算gi、hj(0≤i,j≤2k-1),产生的两个时延需消耗2TX,因此,把此部分特殊公式用“*”表示。此外,对x2k+xk+1进行多项式乘法的模约简运算时,相应的乘法矩阵有部分项需要再做一次加法,这部分项在表中用“?”表示。 表1 R1、R2和Q系数中包含的项数统计 对x2k+xk+1进行多项式乘法的模约简运算采用文献[13]提出的计算方法,通过重新排列计算顺序提高速度。如令k=3,需要进行多项式乘法模约简的算式为C1=A1B1modx6+x3+1,其中A1=a5x5+a4x4+a3x3+a2x2+a1x+a0,B1=b5x5+b4x4+b3x3+b2x2+b1x+b0。因此,该多项式乘法模约简运算的矩阵向量形式为: 由Z矩阵可以看出,有部分项需要多做一次加法,由于是并行计算,因此此处会产生TA+TX的电路门延时。将所有结果都采用分治思想,并借鉴二叉树的思想,将其两两异或、并行迭代。为方便表达,下文将这种运算方法简化表达为异或二叉树,异或二叉树运算过程需要「log2(k+「k/2⎤)⎤=「log25⎤=3 XOR延迟。因此,[AB]x2k+xk+1的时间复杂度最高会达到TA+「log2(3k)⎤TX。实际计算两个子式和时,可采用与文献[8,14]一样的方法,将两个子式合并到一个异或二叉树以提高计算速度。 分别评估R1、R2和Q电路门的延时。从表1可以看出,R1中会产生最多电路门延时的是系数处于r1,m-k-1=sm-2k-1+tm-2k-1时,sm-2k-1是m-2k个项的总和,tm-2k-1需要耗费2TX来计算gi、hi以及1TX用于其中的k项。在此过程中,sm-2k-1的异或二叉树也可以与tm-2k-1的异或二叉树合成一个树并行计算。 TA+「log2((4(5k-m)+2v1))⎤TX, v1=「log2(m-3k)⎤, 同样,做以上相似的分析也可易得其他情况下的时间复杂度: 4k 5k 先对R1、R2、Q的系数进行计算,根据式(9)和式(10)~式(14)可知,主要是: (15) 由于si是AB的系数,因此可以直接得出si的公式为: 得到式(16)中系数表达式的空间复杂度: (2k)2=6k2-2km+m2-k, 乘法器所需的AND电路门的数量等于式(15)中所需的数量,即6k2-2km+m2-k。而XOR电路门的数量通过式(7)和式(12)~式(14)可以看出,需要额外的XOR电路门来计算不同子式和C之间的加法,且需要消耗几个XOR电路门对[A]x2k+xk+1和[B〗x2k+xk+1预计算。最后统计这些操作所需的XOR电路门的数量如下: 因此,乘法器所需的XOR电路门的总数为: 分析以上数据可知,当m>3k时,AND电路门的数量会小于m2,换言之,当m>3k时,设计的乘法器所需逻辑电路门的数量可能比平方级乘法器所需的更少。 文献[10]中设计的CRT乘法器为当前同类不可约五项式乘法器中最主流的研究成果,本文所构造的乘法器与其相比,在时间复杂度略有增加的情况下,空间复杂度有所降低,达到了时间空间复杂度均衡的目的。为了更明显的表达,更进一步地体现比较结果,笔者验证了在[100,1 000]次数内的所有符合不可约五项式xm+xm-k+xm-2k+x+1的结果,并统计成表格。为方便表达笔者将文献[10]中的乘法器以作者首字母缩写命名为LCY。从比较结果中可知,与主流乘法器相比最多会增加2Tx的时延。 为提高有限域乘法运算的速度,扩大乘法器的应用范围,使基于中国剩余定理的乘法器架构更一般化。笔者设计了一个通用公式来搭建基于中国剩余定理的混合乘法器模型,找到一个特殊的不可约五项式f(x)=xm+xm-k+xm-2k+x+ 1,套用通用公式成功将多项式对f(x)的运算转化成对更简单的F(x)的商和余数的计算,其中对余数的计算延用前人的方法采用中国剩余定理,对商的计算创新性地采用了两次求逆的方法。该乘法器将时间复杂度和空间复杂度进行了均衡,得到了较优的结果,在时间复杂度稍大于当前最快的并行乘法算法的前提下,空间复杂度得到了优化,当m>3k时,本文构建的乘法器的空间复杂度比同类型的主流乘法器更低,并且扩大了基于中国剩余定理的乘法器的适用范围。 表2 特殊五项式的复杂度比较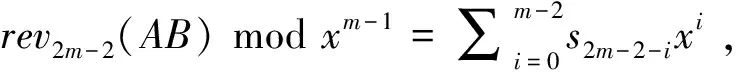
2.2 计算AB关于F(x)的余数R
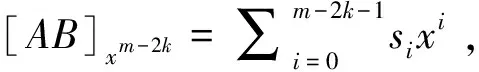



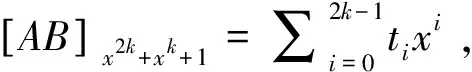
2.3 计算有限域乘法的结果C
3 时间和空间复杂度分析
3.1 时间复杂度分析


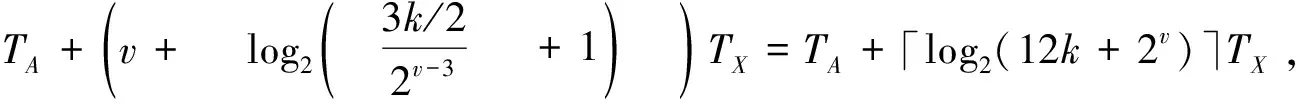
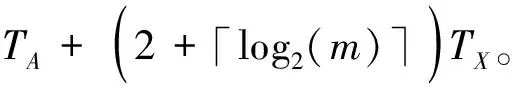


3.2 空间复杂度分析
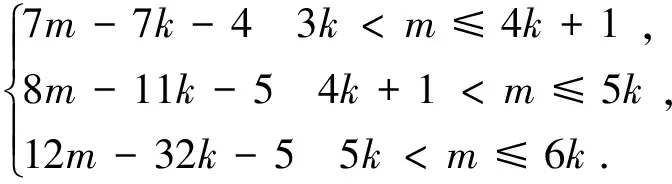
3.3 与主流乘法器的比较
4 结语