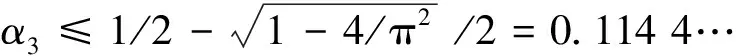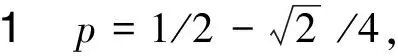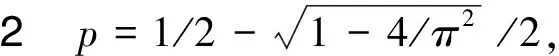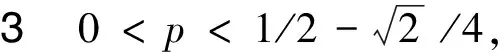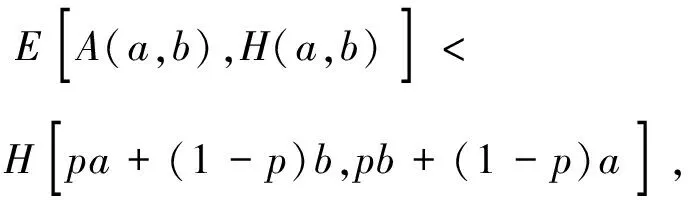特殊拟算术型平均与算术、调和平均的最佳不等式
徐仁旭 徐会作 钱伟茂
(1. 浙江建设职业技术学院 教务处,浙江杭州 311231;2.温州理工学院 数学与信息工程学院,浙江温州 325000;3.湖州广播电视大学 远程教育学院,浙江湖州 313000)
对于r∈(0,1), 第一类和第二类完全椭圆积分κ(r)和ε(r)[1-2]分别表示为
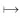
设a,b,c∈R和c≠0,-1,-2,…,高斯超几何函数定义为

众所周知,第一类完全椭圆积分κ(r)和第二类完全椭圆积分ε(r)是高斯超几何函数F(a,b;c;x)的特殊情形[4-5]。实际上有
高斯超几何函数尤其是两类完全椭圆积分在数学理论和工程实践中有诸多重要应用。近年来,相关的学术研究成果不断涌现,在各类设定情形下,国内外学者得出一些完全椭圆积分和高斯超几何函数的重要性质和不等式(参见文献[6-25])。
Toader在文献[6]介绍了一个经典拟算术平均Mp,n(a,b)并且定义如下:
其中p是一个严格单调函数,以及
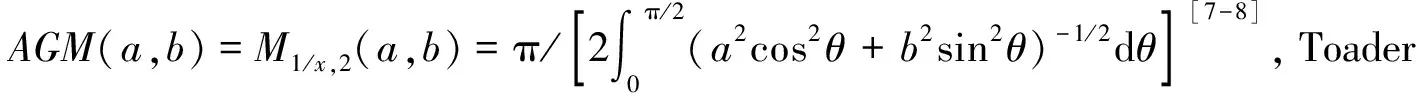

(1)
两个正数a和b的算术平均、调和平均和p阶幂平均分别定义为
(2)
则有不等式
H(a,b)=M-1(a,b) 对所有a,b>0且a≠b成立, 并且双向不等式(参见文献[20],定理19.9.4]) 对所有r∈(0,1)成立。 设 钱伟茂和褚玉明(参见文献[13],推论3.2)得到了双向不等式 H(a,b;λ) 根据二元平均值的定义,显然有 (3) 从不等式(2), 我们淸楚地看到 (4) 对所有a,b>0且a≠b成立。 根据不等式(3)和(4), 我们发现了最佳参数α1,α2,β1,β2∈[0,1]和α3,β3∈[0,1/2]使得双向不等式 α1A(a,b)+(1-α1)H(a,b)< β1A(a,b)+(1-β1)H(a,b), 对所有a,b>0且a≠b成立。 为了证明我们的主要结论,首先需要如下引理。 引理2(参见文献 [3], 定理3.21以及练习3.43) 证明设 (5) 简单计算可得 (6) (7) 从等式(8)和引理2(4)可知 (8) 对所有r∈(0,1)成立。 所以, 引理3容易从等式(6)和(8)得到。 定理1双向不等式 α1A(a,b)+(1-α1)H(a,b)< β1A(a,b)+(1-β1)H(a,b), 对所有a,b>0且a≠b成立当且仅当α1≤4/π2=0.405 2…和β1≥1/2。 证明根据A(a,b),H(a,b)和E(a,b)是对称的且齐次系数为1,不失一般性, 我们假设a>b>0和r=(a-b)/(a+b)∈(0,1),则从等式(1)和(2)得到 H(a,b)=A(a,b)r′2, (9) 根据等式(9)可知 (10) 设f1(r)=4ε2(r)/π2-r′2,f2(r)=r2和 (11) 简单计算可得 f1(0+)=f2(0)=0, (12) (13) (14) 所以,定理 1容易从等式(10), (14)和f(r)的单调性得到。 定理2双向不等式 对所有a,b>0且a≠b成立当且仅当α2≤16/π4=0.164 2…和β2≥1/2。 证明不失一般性, 我们假设a>b>0和r=(a-b)/(a+b)∈(0,1),则从等式(9)得到 (15) 设g1(r)=16ε4(r)/π4-r′4,g2(r)=1-r′4和 (16) 简单计算可得 g1(0+)=g2(0)=0, (17) (18) (19) 所以,定理2容易从等式(15), (19)和g(r)的单调性得到。 定理3双向不等式 证明不失一般性, 我们假设a>b>0,r=(a-b)/(a+b)∈(0,1)和p∈[0,1/2],则从等式(1)和(2)得到 (20) 设 (21) 简单计算可得 h(0+)=0, (22) (23) h′(r)=2rh1(r), (24) 其中 (25) 从引理3和等式(20)得到 (26) h1(1-)=+∞. (27) 下面分四种情形证明: h1(0+)=0. (28) 从引理3,等式(25)和(28)我们清楚地看到 h1(r)>0, (29) 对所有r∈(0,1)成立。 所以, 从等式(20),(21),(22), (24)和不等式(29)容易得 h(1-)=0, (30) (31) 从引理3,(24), (25), (27)和(31)我们知道存在一个实数r0∈(0,1)使得h(r)在区间(0,r0)内是严格单调递减和在区间(r0,1)内是严格单调递增。 所以, 从等式(20),(21),(22), (30)协同h(r)的单调性可得 h1(0+)<0. (32) 由等式(20),(21),(22),(23),(24)协同不等式(32),可知至少有一个充分小实数δ0∈(0,1)使得不等式 对所有a>b>0且(a-b)/(a+b)∈(0,δ0)成立。 h(1-)>0. (33) 等式(20), (21)和不等式(33) 意味着存在一个充分小实数δ1∈(0,1)使得不等式 对所有a>b>0且(a-b)/(a+b)∈(1-δ1,1)成立。 根据定理1~3,我们得到如下三个关于第二类完全椭圆积分ε(r)的不等式。 成立当且仅当α1≤4/π2=0.405 2…和β1≥1/2。 成立当且仅当α2≤16/π4=0.164 2…和β2≥1/2。 推论3对于r∈(0,1),不等式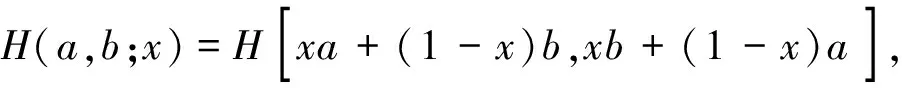
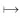
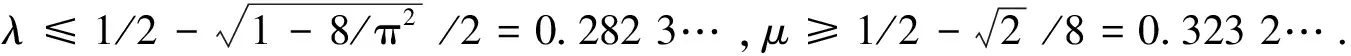
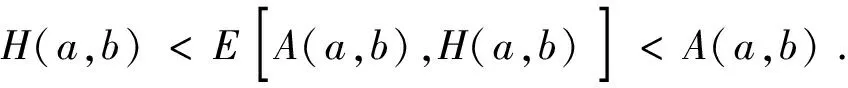

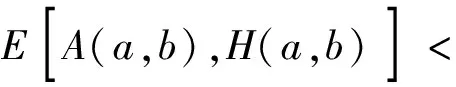
1 主要结果