两圆对对碰，面积最大值——对一道浙江一模题的破解

☉浙江省杭州学军中学 顾 侠

一道好的数学题，凝聚着命题者多少的心血与努力；一道好的数学题，融合了多少数学知识的精华与脉络；一道好的数学题，区分了多少学子的能力与素养；……一道好的数学题，引起了我们高度的热议与深思.

一、问题呈现

问题（2019年浙江某市一模）已知O为坐标原点，圆M：（x+1）2+y2=1，圆N：（x-2）2+y2=4.A，B分别为圆M和圆N上的动点，则S△OAB的最大值为______.

本题目一出现就引起了高度热议，题目设置巧妙，具有极高的水平.巧妙地把圆的方程、圆与圆的位置关系、三角形的面积公式、最值问题等加以链接，同时还隐含着三角函数等相关知识.而且该题还能找到2018年高考真题的原型（2018年全国Ⅰ卷理16），又高于原型，是一道不可多得的原创好题.

二、多解思维

设出相应的角，结合圆的性质得到对应边OA与OB的长度表达式，结合三角形的面积公式加以转化，利用三角恒等变换公式，以及辅助角对三角关系式进行变换，借助三角函数的图像与性质确定相应的最值，进而转化为S△OAB≤2cosβ+sin2β，再利用不同的方法来求解三角关系式的最大值即可.

解法1：如图1，设∠AOM=α，∠BON=β，则有|OA|=2cosα，|OB|=4cosβ，其中

图1

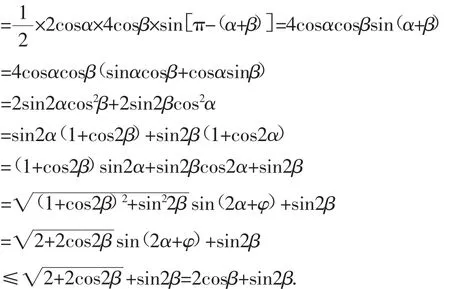
下面确定相应的三角函数的最大值问题，与“（2018年全国Ⅰ卷理16）已知函数f（x）=2sinx+sin2x，则f（x）的最小值是______.”相似，可以从以下不同的角度加以破解.

方 法 1：设f（β）=2cosβ+sin2β，则 有f（β）=2cosβ+2sinβcosβ，可得：

方法2：设f（β）=2cosβ+sin2β，可得f′（β）=-2sinβ+2cos2β=-2sinβ+2（1-2sin2β）=2（1-sinβ-2sin2β）=2（1+sinβ）（1-2sinβ）.

令f（′β）=0，解得或sinβ=-1（舍去），由于β∈可得，所以，即S△OAB的最大值为

方法3：设f（β）=2cosβ+sin2β，

所以S△OAB的最大值为

设出相应的角，结合圆的性质得到对应边OA与OB的长度表达式，结合三角形的面积公式加以转化得到S△OAB=4cosαcosβsin（α+β），结合诱导公式的转化与配凑，凑成可以利用结论“在△ABC中，有sinAsinBsinC≤，当且仅当时等号成立”的情形，从而得以确定相应的最大值问题.

解法2：如图1，设∠AOM=α，∠BON=β，则有|OA|=2cosα，|OB|=4cosβ，其中

所以S△OAB的最大值为

根据几何法进行转化，延长BO交圆M于点C，利用两圆方程所确定的位置与半径得到|BO|=2|CO|，从而根据△OAB与△OAC同高的条件确定S△OAB=2S△OAC，再在圆M内，利用“在圆的所有内接三角形中，等边三角形的面积最大”的结论加以转化与应用，即可确定相应的三角形面积的最大值.

解法3：如图2，作BO的延长线交圆M于点C，结合两圆的方程及性质可得|BO|=2|CO|，则有S△OAB=2S△OAC.

而对于圆的内接△OAC而言，当且仅当△OAC为等边三角形时面积最大，此时等边三角形△OAC的边长为，对应的面积

所以S△OAB的最大值为

图2

三、链接真题

【高考真题】（2018年全国Ⅰ卷理16）已知函数f（x）=2sinx+sin2x，则f（x）的最小值是______.

四、规律总结

在求解一些具有一定代表性、典型性的数学问题时，要学会认真分析——题目条件与结论，仔细研磨——解题方法与技巧，细心探究——变式拓展与探究，耐心串联——高考真题与变形，进而真正达到“认真解答一个题，拓广解决一类题，变式深化一片题，链接串联一整片，能力素养一起高”的目的.