对一道立几题的多解、变式及延伸

☉甘肃省高台县第一中学 王学成

立体几何中的空间角（线线角、线面角与二面角等）问题，能够比较集中地考查学生的空间想象能力，还能有效地考查逻辑推理、直观想象与数学运算等相关的核心素养，历年来为高考命题者所垂青，几乎每年必考.而异面直线所成的角也是其中重要的一个部分，破解方法灵活多样，问题背景与设问角度千变万化，是空间角的考查过程中的一个活跃因素.

一、问题呈现

例题（2018年上海卷17）已知圆锥的顶点为P，底面圆心为O，半径为2.

（1）设圆锥的母线长为4，求圆锥的体积；

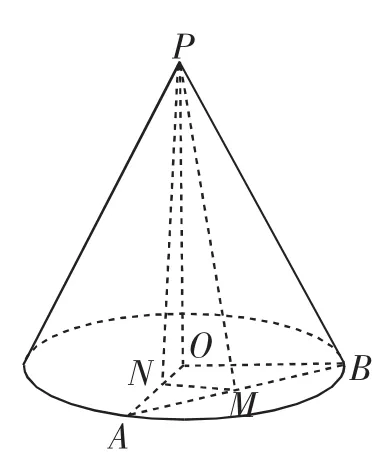
图1

（2）设PO=4，OA、OB是底面半径，且∠AOB=90°，M为线段

AB的中点，如图1所示.求异面直线PM与OB所成角的大小.

本题以圆锥为空间几何体的背景，通过求解圆锥的体积及异面直线所成的角来设置问题.而借助异面直线所成的角进一步拓展与变形，可以转化为求解直线与平面所成的角或二面角的平面角等空间角问题.

二、多解思维

解析：（1）由于圆锥的顶点为P，底面圆心为O，半径为2，圆锥的母线长为4.

（2）由于PO=4，OA、OB是底面半径，且∠AOB=90°，M为线段AB的中点.

求解异面直线PM与OB所成角的大小，可以从以下不同的思维角度来入手：

角度1：取OA的中点N，利用MN∥OB，抓住异面直线所成角的定义，即可确定∠PMN即为异面直线PM与OB所成的角.再通过求解三角形来进行化归与转化，结合余弦定理的应用即可达到求解的目的.

解法1：取OA的中点N，连接PN、MN，而M为线段AB的中点，则知MN∥OB，且，根据异面直线所成角的定义可知∠PMN即为异面直线PM与OB所成的角.由于，在△PMN中，由余弦定理可得，即所以异面直线PM与OB所成角的大小为

点评：利用平移法求解异面直线所成角是破解异面直线所成角中比较常见的一类几何法，具有一定的可操作性，且有规律可循.在具体的平移法求解过程中，最常见的是抓住几何体中的一些特殊点（如线段中点、线段分点、线段交点、线段已知点等），利用异面直线所成角的定义合理地构造异面直线所成的角，再结合相关的知识来分析与求解即可.

角度2：根据所求异面直线中两直线所对应的向量，其中，结合空间向量的数量积公式加以转化得到的值，结合异面直线所成角的条件，利用公式来求解并确定相应的角即可.

解 法2：根据题意可得，则有cos45°=2.设异面直线PM与OB所成的角为θ，则cosθ=，即θ=，所以异面直线PM与OB所成角的大小为

点评：利用基底法求解异面直线所成角是破解异面直线所成角中比较常见的一类方法，破解的关键是根据题目条件选择恰当的基底向量，通过空间向量的线性关系与线性运算进行化归与转化，进而表示成相应的基底向量的线性关系，再结合空间向量的数量积公式来确定对应的空间向量的夹角，并结合异面直线所成角的取值情况加以对比来确定即可.

角度3：结合PO垂直于底面圆，同时∠AOB=90°，则可以以O为原点，OA为x轴，OB为y轴，OP为z轴，建立空间直角坐标系O-xyz，再将异面直线PM与OB所对应的空间向量与用坐标的形式表示出来，最后利用空间向量的数量积的坐标运算公式来处理即可.

图2

解法3：由于PO=4，OA，OB是底面半径，且∠AOB=90°，M为线段AB的中点，所以以O为原点，OA为x轴，OB为y轴，OP为z轴，如图2所示，建立空间直角坐标系O-xyz，则P（0，0，4），A（2，0，0），B（0，2，0），M（1，1，0），O（0，0，0）.设异面直线PM与OB所成的角为θ，则，即，所以异面直线PM与OB所成角的大小为

点评：利用坐标法求解异面直线所成角是官方给出的标准参考答案，也是破解异面直线所成角中比较常见的方法.利用坐标法解决此类问题时，关键是建立恰当的空间直角坐标系，利用空间向量的数量积的坐标运算的夹角公式来分析与求解，要求计算准确.设异面直线PM与OB所成的角为θ，则有要特别注意的是异面直线所成的角与空间向量的夹角之间的关系，有时两者并不吻合.

三、变式探究

探究1：保留题目背景，改变原来求解异面直线所成的角为直线与平面所成的角，从而得到以下变式：

变式1：已知圆锥的顶点为P，底面圆心为O，半径为2.

（1）设圆锥的母线长为4，求圆锥的体积；

（2）设PO=4，OA、OB是底面半径，且∠AOB=90°，M为线段AB的中点，如图1所示.求直线PM与圆锥底面所成角的大小.

解析：（1）同真题（1）的解析.

（2）连接OM，根据直线与平面所成角的定义可知∠PMO即为直线PM与圆锥底面所成的角，由于PO=4，OA、OB是底面半径，且∠AOB=90°，M为线段AB的中点，可得，在Rt△POM中即，所以直线PM与圆锥底面所成角的大小为

探究2：保留题目背景，改变原来求解异面直线所成的角为二面角的平面角问题，从而得到以下变式：

变式2：已知圆锥的顶点为P，底面圆心为O，半径为2.

（1）设圆锥的母线长为4，求圆锥的体积；

（2）设PO=4，OA、OB是底面半径，且∠AOB=90°，M为线段AB的中点，如图1所示.求二面角P-AB-O的平面角的大小.

解析：（1）同真题（1）的解析.

（2）连接OM，由于PO=4，OA、OB是底面半径，且°，M为线段AB的中点，可得AB，又PO垂直于圆锥底面，结合三垂线定理及其逆定理可知PM⊥AB.

根据二面角的平面角定义可知∠PMO即为二面角P-AB-O的平面角，在Rt△POM中，即，所以二面角P-AB-O的平面角的大小为

四、规律总结

涉及立体几何中的空间角（线线角、线面角与二面角等）问题，破解的方式可以从几何法的角度进行合理的平移法、补形法的应用，也可以从向量法的角度进行合理的基底法、坐标法的应用.几何法重逻辑推理与数学运算，而向量法重空间想象与数学运算.无论采用哪种破解方式，都可以达到解决问题的目的，解决问题的关键是充分考虑题目条件，通过空间想象能力、运算求解能力的应用来综合处理.