巧用“画图”学数学

《义务教育数学课程标准（2011年版）》指出：几何直观可以帮助学生直观地理解数学，在整个数学学习过程中都发挥着重要作用。画图也是一种几何直观，旨在借助图形帮助学生直接感知与认识事物的性质或数量关系。数学家希尔伯特在《直观几何》一书中指出：图形可以帮助我们发现、描述研究的问题；可以帮助我们寻求解决问题的思路；可以帮助我们理解和记忆得到的结果，这就是图形带给我们的好处。在实际教学中，我们发现，学生普遍缺乏画图的意识与能力，遇到较为复杂的问题，很少会主动想到用画图的方式来帮助思考和解答。由此看来，研究画图的妙用有其独特的现实意义。

1.加深概念理解，凸显本质。

概念在数学教学中有着举足轻重的作用。在日常教学中，我们常常发现，有些概念如果仅仅依靠文字叙述，学生理解起来比较困难，即使记住了结论，也常常是知其然而不知其所以然。借助画图法来帮助学生理解概念的本质，则能产生意想不到的教学效果。

例如：教学苏教版五上《小数的近似数》一课，教师出示练习题：写出4.96的近似数（精确到十分位）。学生出现了两种答案——5和5.0，教师组织学生讨论，发现大多数学生都同意近似数是5.0，但不少学生只是基于题目要求“精确到十分位”而认为近似数末尾的0不能去掉。学生是否真正了解近似数5.0和5的区别呢？于是，教师追问：近似值取5.0与5有区别吗？大多数学生面露难色沉默不语，只有几个学生表示5.0与5的精确度不同。其实，这个问题对学生来说用语言表述起来确实比较困难，为了帮助学生理解，教师呈现图1、图2引导他们进行对比。从图中能清楚地看出：近似数5.0的取值范围介于4.95—5.04之间，而近似数5的取值范围介于4.5—5.4之间，很好地解释了为什么近似数5.0比5更加精确。以后，学生也就不会再随意去掉近似数末尾的0了。可见，用画图法表述概念，使概念的呈现变得简单、直观，便于学生观察和理解，认清概念本质。

（图1）

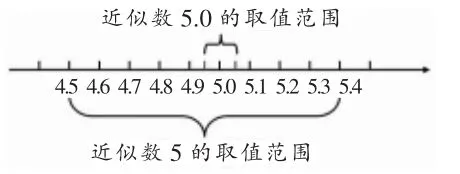
（图2）

2.有效突破难点，化难为易。

在教学中，我们常常发现，有些教学难点教师反复讲解很多遍却还是收效甚微，学生要么当时听懂了隔段时间又忘记了，要么只会死记方法而不会灵活运用。这是由于学生对这些知识点的认识只是浮于表面，而没有从根本上去理解。对于一些教学难点，教师不妨采用画图的方法辅助教学，促进学生理解知识本质。

例如：教学苏教版四下《解决问题的策略：画图》一课，有这样一个问题：一个正方形的边长是4分米，如果把对边增加1分米，面积增加多少平方分米？如果把邻边增加1分米呢？学生对“对边”和“邻边”的理解往往是学习的难点，通过画图（如图3、图4）则能很好地帮助学生突破这个难点。

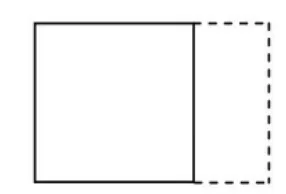
图3 对边增加

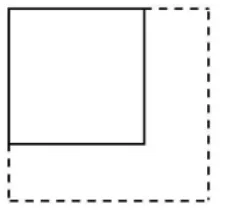
图4 邻边增加

学生能从两幅图中直观地看出“对边”和邻边”的区别，增加部分的面积也直观地呈现在学生眼前，对边增加时只要用增加的长度×原有边长即可，邻边增加时则需要用分割法或用现有的大面积减小面积。

3.发掘多样方法，提升思维。

画图法有助于学生从图中寻找新的灵感，从而想出多种方法解决同一问题，促使他们在探索、对比和交流多种方法的过程中，不断加深对问题的认识和对方法的理解，从而促进他们数学思维的发展。

（图5）

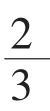
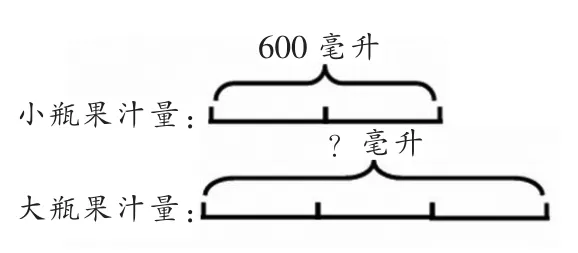
（图6）

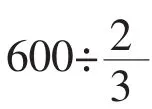
小学生的思维正处于从具体形象思维向抽象逻辑思维过渡的阶段，通过画图能使复杂的问题变简单、抽象的问题变具体。学生在画图过程中能逐步体会到图形的优势，找到一些在文字表述中不易发现的潜藏性内容，从而发现解题思路，渗透数形结合、对应、转化等数学思想，这些都是学生可持续发展的动力和源泉。