几类代数不等式的三角背景*
(宏实中学,安徽 枞阳 246700)
代数不等式是数学竞赛中一种不可或缺的题型.那些精美的不等式往往使人绞尽脑汁,但又让人爱不释手.在敬佩、感叹之余,人们心中往往会产生疑惑:这些不等式是怎么想到的,有没有证明的捷径?笔者发现,代数不等式有几种常见的三角背景,本文借用数学竞赛、期刊杂志和安振平新浪博客中的代数不等式,对几类常见代数不等式的三角背景作一个总结,供大家参考.

证明在△ABC中,
当且仅当△ABC为正三角形时等号成立[1].

证明设x=tanA,y=tanB,z=tanC,其中A,B,C为锐角△ABC的3个内角,则

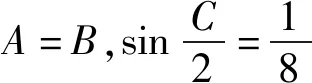
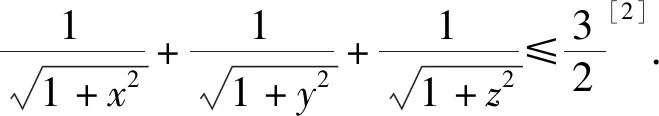
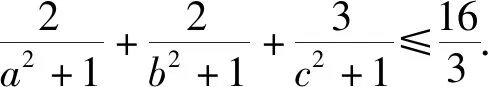
(《数学通报》2018年9月数学问题2 442)
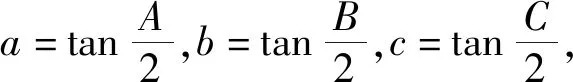
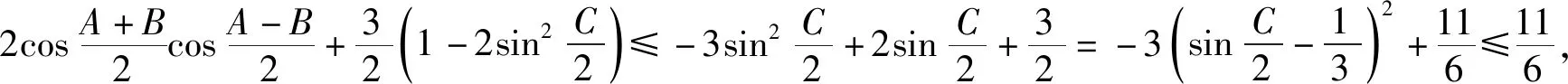
背景2在△ABC中,cosA+cosB+cosC≥2(cosAcosB+cosBcosC+cosCcosA).
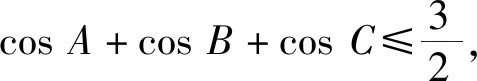

即
cosA+cosB+cosC≥2(cosAcosB+cosBcosC+cosCcosA),
当且仅当△ABC为正三角形时等号成立[3].
例3已知a,b,c≥0,a2+b2+c2+abc=4,求证:a+b+c≥ab+bc+ca.
(安振平新浪博客不等式问题4 712)
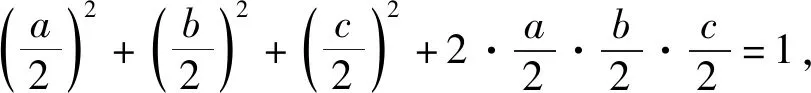
cos2A+cos2B+cos2C+2cosAcosBcosC=1,
令2cosA=a,2cosB=b,2cosC=c,则所证的式子转化为
cosA+cosB+cosC≥2(cosAcosB+cosBcosC+cosCcosA).
应用背景2,即证.

(2011年中欧数学奥林匹克竞赛试题第2题)

cos2A+cos2B+cos2C+2cosAcosBcosC=1,
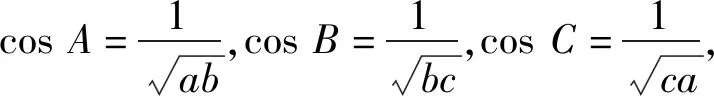

当且仅当a=b=c=1时等号成立.

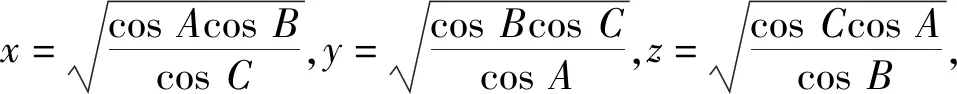
当且仅当△ABC为正三角形时等号成立.
例5已知x,y,z>0,xy+yz+zx+xyz=4,求证:x+y+z≥xy+yz+zx.
(1996年越南数学奥林匹克竞赛试题第3题)
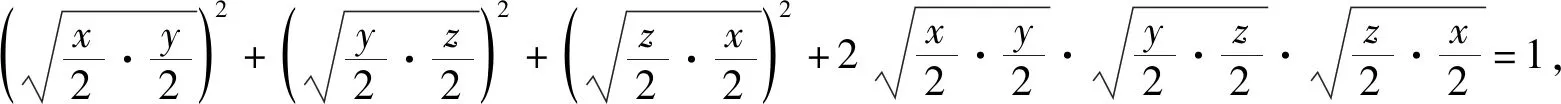
结合背景3,即证.

(安振平新浪博客不等式问题4 714)
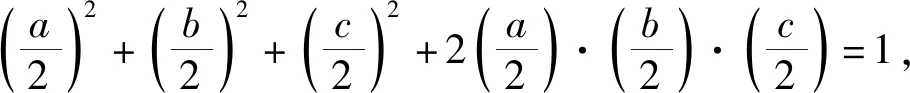
cos2A+cos2B+cos2C+2cosAcosBcosC=1,
构造锐角△ABC.令2cosA=a,2cosB=b,2cosC=c,则原式转化为
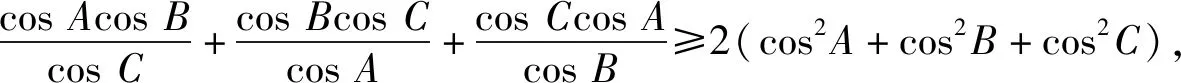
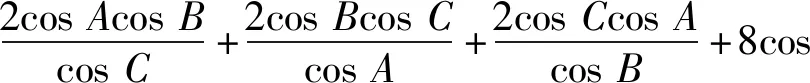
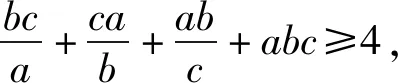
当且仅当a=b=c=1时等号成立.
总之,从代数式的结构出发,对代数不等式问题的三角背景进行挖掘,新颖复杂的代数不等式往往就转化为优美整洁的三角不等式,从三角的视角去研讨问题,为问题的解决找到了一条“柳暗花明又一村”的捷径.

