“分”的巧妙 解的精彩*——导数证明不等式策略的探究

(池州市第一中学，安徽 池州 247000)

用导数证明不等式的技巧往往比较灵活，本文主要探究用“分”的技巧证明不等式.“分”的技巧主要有以下7个：分常、分函、分参、分类、分元、分隔、分拆，这些技巧是证明有关不等式的利器和法宝，对思维有很大的启发作用，值得我们思考并加以总结.

1 分常

分常，指的是分离“常数”.有些问题中，如果把式子中的某个关键的“常数”分离出来，问题求解就会变得简单、巧妙.

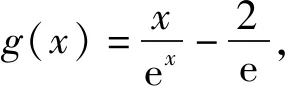
因为函数f(x)与g(x)的最值点不同，所以

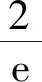
2 分函

分函，指的是分离“函数”.这个函数主要指的是两个特殊的函数：①y=lnx，②y=ex，这两个函数可以说是最为重要、最为活跃的函数，它们出现的频率很高，很多问题都涉及这两个函数.我们在解决这类问题时，常常要把这两个函数分离出来，使问题求解变得简单.

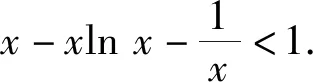
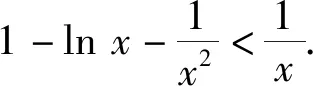
则

易知f′(x)在(0,2)上单调递减，在(2,+∞)上单调递增，从而

于是

f(x)>0,

故

评注本题就是将函数lnx分离出来，这样求导后的导函数就是幂函数，使问题求解变得简单.

3 分参

分参，指的是分离“参数”.含参数的问题是最为常见的问题之一，解决这类问题有一个很重要的方法就是分离参数，分离参数最大的好处就是避免繁杂的讨论.

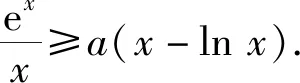
则

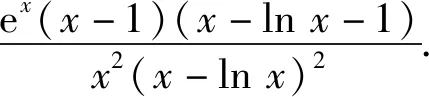
易知

x-lnx-1≥0，

从而当01时，F′(x)>0，于是F(x)在(0,1]上单调递减，在(1,+∞)上单调递增,故

F(x)≥F(1)=e.

又a≤e，从而

f(x)≥a，

命题得证.

评注本题就是通过分离参数，使问题求解变得简单.

4 分类

分类，指的是分类讨论.这也是解决问题的常用方法，而且是高考几乎必考的方法之一，考查学生的思维能力，难度一般较大.

对于例3，下面利用分类讨论的方法求解.

证法2由题意知定义域是x>0.令

则

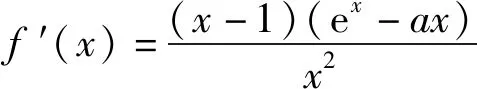
1)若a≤0，则

ex-ax>0，

从而

f(x)min=f(1)=e-a>0.

2)若1

h(x)=ex-ax，

则

h′(x)=ex-a,

易知h(x)在(0,lna)上单调递减，在(lna,+∞)上单调递增，从而h(x)min=h(lna)=a-alna=a(1-lna)≥0,于是f(x)在(0,1]上单调递减，在[1，+∞)上单调递增，故

f(x)min=f(1)=e-a≥0.

3)若0

h′(x)=ex-a>1-a>0,

从而h(x)在(0,+∞)上单调递增,于是

h(x)>h(0)=1>0,

进而f(x)在(0,1]上单调递减，在[1,+∞)上单调递增，故

f(x)min=f(1)=e-a>0,

综上可知f(x)≥0，命题得证.

g(x)min=g(1)=e，

进而

故

ex≥ax.

可见，本题“分参”比“分类”要简单.

5 分元

分元，指的是一个式子中如果含有多个变量，可以将其中一个变量作为主元，即所谓的“主元思想”.这种方法也是解决问题的一个重要方法，如果能够巧妙运用，可使问题解决变得简单.

对于例3，下面利用分元的方法进行证明.

易知ex-ex≥0，从而g(x)在(0,1]上单调递减，在[1,+∞)上单调递增，于是

g(x)min=g(1)=e-e=0，

进而

g(x)≥0，

即

命题得证.

评注证法3用到了分元，即“主元思想”的运用，这是处理多元变量的常用方法.从本题的解答中，还可以得出这样一道变式题“求证：ex≥e(x2-xlnx)”.此题如果从分离函数的角度去考虑，是分离函数ex还是分离函数lnx？证法3实际上就是分离函数lnx，若分离函数ex，则证明比较困难，要用到三阶求导，且需要敏锐地观察出零点x=1.由此可见，一般情况下，如果一个式子中既有lnx又有ex，分离lnx比分离ex好，这是值得我们注意的地方.

6 分隔

分隔，就是找到一条直线或一条曲线，将两个函数图像分隔开来，一个在直线的上方，另一个在直线的下方，从而使问题顺利求解.这种方法在解决有关问题时比较简单.

例4求证：ex>ln(x+2).

证明因为x>-2,易知ex≥x+1(等号成立的条件是x=0)，ln(x+1)≤x，所以

ln(x+2)≤x+1(等号成立的条件是x=-1)，

从而

ex≥ln(x+2).

又等号成立的条件不同，故ex>ln(x+2).

评注本题就是找到一条隔离直线y=x+1，将函数y=ex与函数y=ln(x+2)隔离开来，函数y=ex在隔离直线y=x+1的上方，函数y=ln(x+2)在隔离直线y=x+1的下方，从而使问题巧妙得证.本题如果不用隔离直线的方法，直接构造函数f(x)=ex-ln(x+2)，证明比较复杂.

7 分拆

分拆，指的是将题目所给的函数拆成几部分，然后对每一部分分别求最值.这种方法在解决比较复杂的函数时效果明显，因此分拆也是解决有关问题的好方法.

在数学教学中，教师要引导学生做好“学思行”.学而不思则罔，善于思考、乐于思考是重要的学习品质，在问题求解中，不能浅尝即止，要深入反思、勤于总结、深度探究，力求有新发现，还要注重合作学习、探究学习、创新学习，力求高观点、大格局.