悟向量四通法 破高考八方题*
(浙江师范大学附属中学,浙江 金华 321004)
1 向量的特点
向量是几何与代数交汇的数学知识,融“数”“形”于一体[1].一方面向量有大小、坐标表示、数量积等代数特征;另一方面向量有图形、方向、夹角等几何特征.向量广泛运用于函数、不等式、立体几何、解析几何等,在处理长度、角度、位置关系等问题中具明显优势.向量是数形结合的有效工具,当向量问题无法直接处理时,通常可转化为数或形使问题变得简洁明了.因此,向量问题蕴含“数形结合”“转化化归”思想,有利于提升学生直观想象、数学运算、数学抽象等核心素养,有利于培养学生良好的思维品质.
先从运算说起,设a=(x1,y1),b=(x2,y2),其中x1,x2,y1,y2∈R,则相关运算如表1所示.

表1 向量的相关运算
向量的多种运算启示我们,在处理向量问题时可使用直接法、数形结合(图解法)、坐标法、基向量法等方法.

图1
2 问题展示

(2019年浙江省数学高考试题第17题)
此题的特点:1)形式复杂但运算单一,全为数乘向量,λi只有两个值;2)图1为边长是1的正方形,虽简约但各边和对角线同时出现,分量重.
思路1向量太多,可否变得集中些?
考虑用基向量法:



图2
思路2正方形ABCD比较适合通过建系进行坐标运算,采用坐标法.
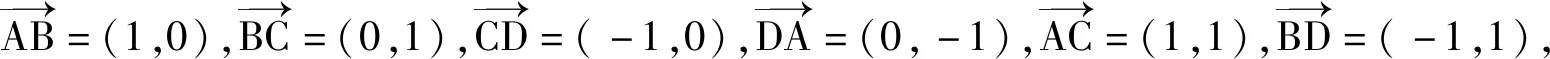
接下去与思路1相同.

3 各显神通
为凸显各法的特点以及使用条件,笔者将2019年全国高考卷中所有向量考题一一归类,辅以部分历年有代表性的高考题,通过分析各种题型特征,为求解向量问题快速找到突破办法.
3.1 直接法
例2已知向量a=(-4,3),b=(6,m),且a⊥b,则m=______.
(2019年北京市数学高考文科试题第9题)
分析因为a⊥b,所以a·b=-4×6+3×m=0,得m=8.向量a,b的坐标已知,故可直接利用数量积公式运算.
例3已知非零向量a,b满足|a|=2|b|,且(a-b)⊥b,则a与b的夹角为
( )
(2019年全国数学高考卷Ⅰ理科试题第7题、文科试题第8题)

分析此题涉及的知识点有:1)b2=|b|2;2)(a-b)⊥b,则(a-b)·b=0;3)向量的夹角公式.
以上知识均属《2019年普通高等学校招生全国统一考试说明》中的“掌握”内容,因此该题无需数形结合或者转化为坐标,属直接法.
类似的考题还有:
例4已知向量a=(2,2),b=(-8,6),则cos
(2019年全国数学高考卷Ⅲ文科试题第13题)

(2019年全国数学高考卷Ⅲ理科试题第13题)
例6已知向量a=(2,3),b=(3,2),则|a-b|=
( )
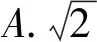
(2019年全国数学高考卷Ⅱ文科试题第3题)

( )
A.-3 B.-2 C.2 D.3
(2019年全国数学高考卷Ⅱ理科试题第3题)
3.2 数形结合

( )
A.充分而不必要条件 B.必要而不充分条件
C.充分必要条件 D.既不充分也不必要条件
(2019年北京市数学高考理科试题第7题)
图3
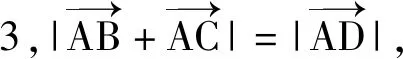
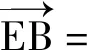
( )
(2018年全国数学高考卷Ⅰ理科试题第6题)
例10已知平面向量a,b(其中a≠0,a≠b)满足|b|=1,且a与b-a的夹角为120°,则|a|的取值范围是______.
(2010年浙江省数学高考理科试题第16题)
此外,采用数形结合法解决的向量问题中部分还可以使用“投影法”或“等值线法”快速解决.
3.2.1 投影法

( )
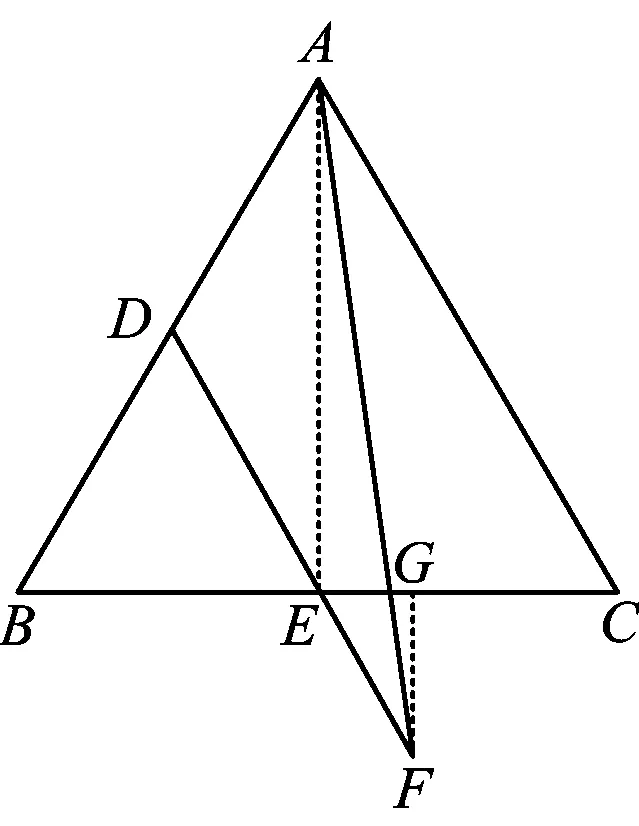
图4
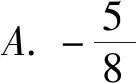
(2016年天津市数学高考理科试题第7题)

3.2.2 等值线法
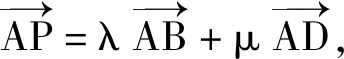
( )
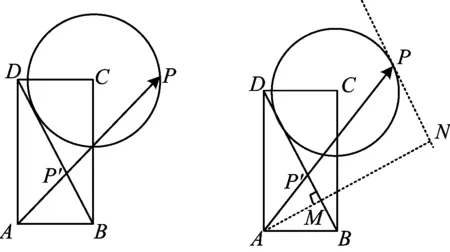
图5 图6
(2017年全国数学高考卷Ⅲ理科试题第12题)
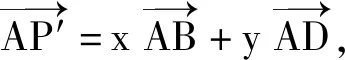
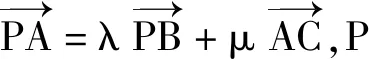
共线定理中的3个向量的特点是同起点,若具备λ+μ=1,则3个向量的终点共线,因为只要点A在直线BC上,均有λ+μ=1,所以直线BC可称为λ+μ的等值线.若点A在另一条与BC平行的直线上运动,则λ+μ的值也保持不变.
3.2.3 坐标法
2019年数学高考题中需转化为坐标法求解的考题不多,天津卷第14题可以用坐标法解决.这里再列举几个历年考题.
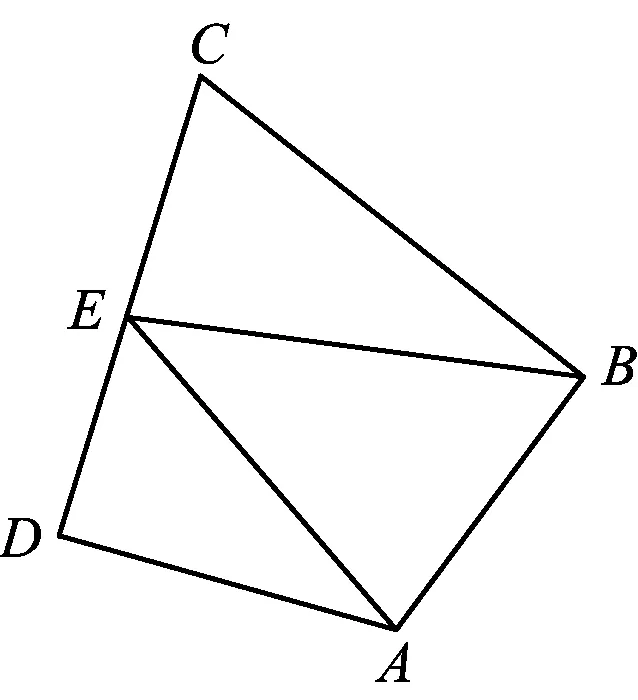
图7

( )
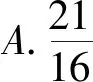
(2018年天津市数学高考理科试题第8题)

此题中有AB⊥BC,AD⊥CD,垂直是建系的一种“暗号”,提醒我们如果直接法或者图形运算不能做出来的时候,可以通过建系转化为坐标运算,再转化为代数问题.
历年高考卷中可用坐标法解决的考题还有:

( )
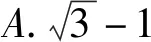
(2018年浙江省数学高考试题第9题)

( )
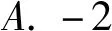
(2017年全国数学高考卷Ⅱ理科试题第7题)

图8
3.2.4 基向量法

(2019年江苏省数学高考试题第12题)
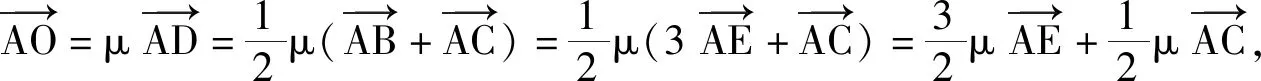
当一个考题中向量个数多显得“杂乱”时,可选取适当的基底,将所有向量转化为基底表示,最后变为两个向量的问题,进行“瘦身”运动.
可用基向量法解决的考题还有:
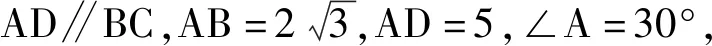
(2019年天津市数学高考文、理科试题第14题)

(2012年浙江省数学高考理科试题第12题)
向量的多种运算形式已在前面详细说明,下面对各种解法适用的特征做简单小结:
1)不管涉及向量的字母运算、图形运算还是坐标运算,凡是在求模、夹角、数量积中可由题中条件直接得出结果,不需要另外建系、画图或者分解之类的,都属于直接法.
2)图形语言描述向量问题可使问题变得直观,如a·b=0表达垂直,|a-b|=1表达两点间距离,|a|=1且a·b=1,则表达投影.以上信息,均可用向量的图形语言表达,有时“取值范围”的问题用图形运算特别合适,体现“数形结合”法的优势.
3)坐标法与图形语言不同,坐标法是将向量问题转化为代数问题处理,使用坐标法得先判断建系与向量的坐标表示是否便捷.
4)问题中出现多个不同向量时,可选取适当的基底,将所有向量用基底表示,进行“瘦身”运动,最后变为两个向量的问题.
当然,很多时候,光靠某一种解法可能还不够,可将以上方法综合应用,如文中例1需要数形结合、直接法、坐标法等多种方法结合才能解决.
4 教学建议
向量问题中蕴涵丰富的数学思想、方法,是认识数学本质、发展核心素养、培养数学思维、提高四基四能的重要载体.因为向量问题表达抽象、方法灵活,所以很多学生都畏惧.但通览近几年的向量问题,均可用上述方法解决,说明向量问题有章法可循,因此笔者提供的教学建议是:1)要求学生掌握向量的3种运算,熟记平行、垂直的向量表达公式,这是基础;2)教学时应引导学生深入理解向量的特征,从符号语言、图形语言、坐标语言等角度分析向量问题,及时归类和巩固,培养学生一题多解、多题一解的能力,进而掌握以上4种通法.

