从一道高考解析几何试题产生联想*
(太湖中学,安徽 太湖 246400)
1 试题分析

1)若|AF|+|BF|=4,求直线l的方程;
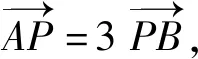
(2019年全国数学高考卷Ⅰ理科试题第19题)
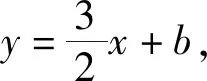
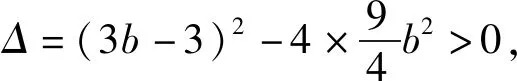
即
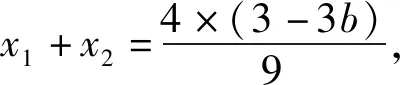
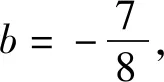
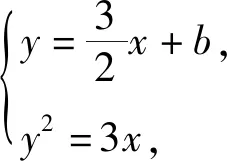
y2-2y+2b=0,
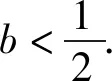
y1=-3y2.
又y1+y2=2,y1y2=2b,从而
y1=3,y2=-1,

说明本题虽然难度不大,但解析几何中的设点设线、联立消元、韦达定理、根的判别式Δ>0、条件转换(包括向量关系代数化、斜率关系、中点关系、弦长公式和活用定义等),都在解题过程中得到了很好的体现,并对解析几何中一些重要的思想方法进行了有效考查.
2 联想探究
2.1 逆向联想
对上题中的第1)小题作逆向思考,题设与结论互换得到:
联想1[1]已知抛物线C:y2=3x的焦点为F,直线l:12x-8y-7=0与C的交点为A,B,求|AF|+|BF|.
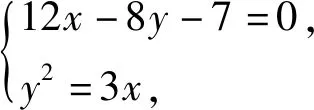
144x2-360x+49=0,
从而
于是
2.2 特殊联想
将直线l特殊化,它经过焦点F,得到:
联想2已知抛物线C:y2=3x的焦点为F,直线l经过点F,且与C的交点为A,B.若|AF|+|BF|=4,求直线l的方程.
分析设A(x1,y1),B(x2,y2),直线l的方程为
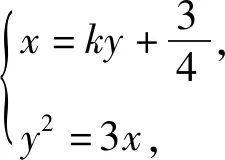
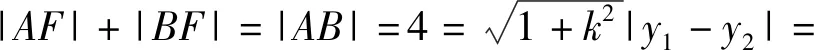

2.3 引申联想
将直线斜率一般化,得到:
联想3已知抛物线C:y2=3x的焦点为F,斜率为k的直线l与C的交点为A,B.若|AF|+|BF|=4,求直线l的方程.
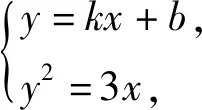
k2x2+(2kb-3)x+b2=0,
由Δ=(2kb-3)2-4×k2b2>0,得
因为|AF|+|BF|=4,所以
即
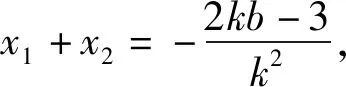
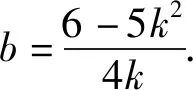
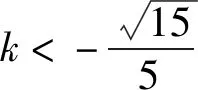
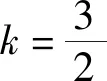
将抛物线一般化,得到:
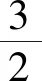
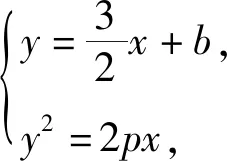
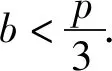
x1+x2+p=4.
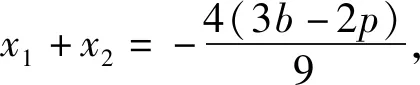
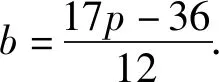
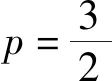
将直线斜率和抛物线都一般化,得到:
联想5已知抛物线C:y2=2px(其中p>0)的焦点为F,斜率为k的直线l与C的交点为A,B.若|AF|+|BF|=4,求直线l的方程.
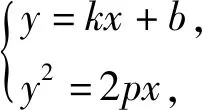
k2x2+(2kb-2p)x+b2=0,
由Δ=(2kb-2p)2-4k2b2>0,得p>2kb.因为|AF|+|BF|=4,所以
x1+x2+p=4.
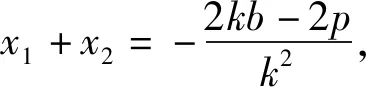
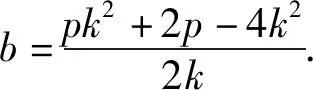
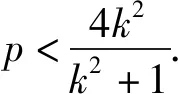
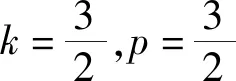
2.4 类比联想
从抛物线向椭圆类比,得到:
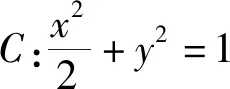
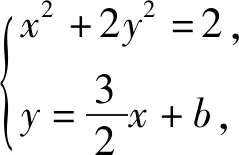
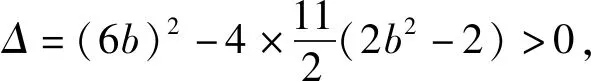
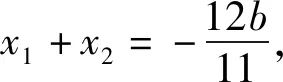

从抛物线向双曲线类比,得到:
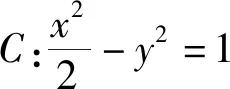
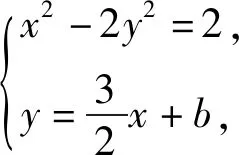

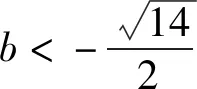
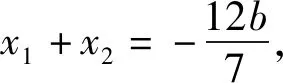
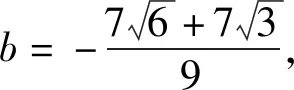
2.5 混合联想
从特殊化、类比两者混合联想得到:
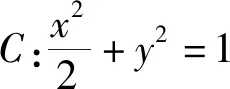
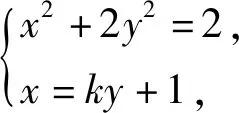
(k2+2)y2+2ky-1=0,
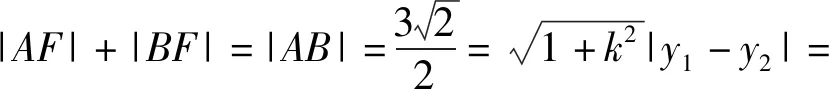
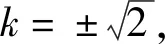
从引申、类比两者混合联想得到:
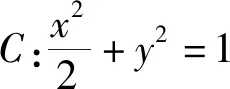
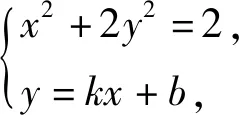
(1+2k2)x2+4kbx+2b2-2=0,
由Δ=(4kb)2-4×2(1+2k2)(b2-1)>0,得
b2<2k2+1.
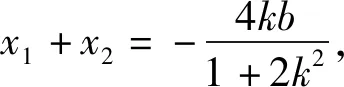
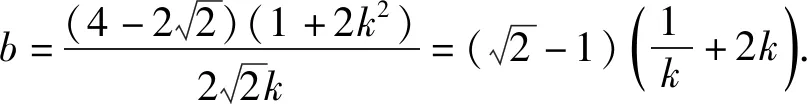
代入b2<2k2+1,得
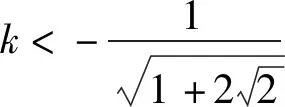
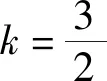
从引申、类比两者混合联想又得到:
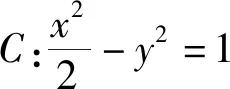
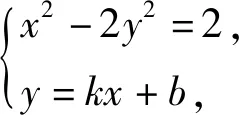
(1-2k2)x2-4kbx-2b2-2=0,
由Δ=(4kb)2+4×2(1+2k2)(b2+1)>0,得
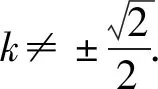

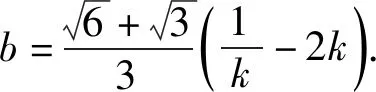
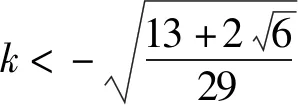
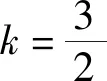
以上从一道高考题出发,通过多侧面、多方向、多角度思考得到10个联想.在整个探究过程中,融观察、类比、猜想、证明于一体,3种圆锥曲线之间内在规律的和谐美、对称美和统一美尽现其中.这给我们的启示是:好的高考题往往具有针对性、示范性和拓展性,如果就题论题,就很难发现其联系、差异、规律和本质,如果认真思考、认真研究、认真比较,通过逆向联想、特殊联想、引申联想、类比联想、混合联想等等,就能得到很多有价值的东西.数学教师在教学中若能恰当运用上述方法,则能有效培养学生思维的发散性、深刻性、广阔性和创新性,促使学生的思维能力和解题水平达到一个新的高度[3].

