边际条件随机占优下的增强型指数投资组合模型

李倩 吴昊

摘要： 本文给出了一个基于边际条件随机占优规则的增强型指数投资组合模型。该模型在均值方差分析框架的基础上引入了边际条件随机占优的两层优化，其中，层次一以约束条件的形式加入模型，使得投资组合在占优于基准指数的边际条件随机占优效率集中;层次二是在多个投资组合中寻找占优程度最高的投资组合，因此在本研究的模型中处理为目标函数。占优程度在本文中定义为边际条件随机占优相对于基准指数的统计量的均值。本文使用多目标免疫算法对该模型进行求解，并应用8个世界主要市场的指数及其成份股数据进行了测试。结果显示本文提出的基于边际条件随机占优规则的指数投资组合能够显著地增强其收益。

关键词： 投资组合; 增强型指数投资; 边际条件随机占优; 均值方差; 多目标优化

文献标识码： A  文章编号： 1002-2848-2019（04）-0118-11

一、问题的提出

指数化投资理念产生于20世纪70年代，是以跟踪或复制某一市场指数为目标，通过分散投资于目标指数的成分证券来最小化交易成本并取得市场平均收益率的一种投资模式。从诞生至今的40年间，出现了各种指数投资产品，包括指数基金、交易型开放式指数基金ETF、股指期货、股指期权、指数联动型债券和存款等。以指数基金和ETF为例，近10年来全球市场以每年40%的速度增长。据Wind资讯数据统计，截至2017年底，我国开放式指数基金产品数量超过600只，资产规模6118.15亿元，产品数量占全市场的比例为8.36%。

近年来，随着指数化投资的繁荣，指数化投资产品的竞争日益加剧，尤其对于指数基金来说，如何通过高收益吸引投资者，从而做大指数基金规模，成为指数型基金管理的重大课题。因此，试图在跟踪指数的同时获得超额收益的增强型指数投资越来越受到市场的青睐和投资者的关注，逐渐成为了新的研究热点。从风险的角度来看，由于将指数的风险分布作为参考，增强型指数投资是一种指数追踪策略。然而，从回报的角度来看，增强型指数投资也是一种主动管理策略，因为它的目标是为了获得超过基准的收益。因此，增强型指数投资有时被称为“风险控制下的主动投资组合管理”。

对增强型指数投资的研究通常在“均值方差”（Mean-Variance，MV）的优化框架下，投资组合选择的目标通常包括两部分：最大化超额收益和最小化追踪误差。由于求解此类问题属于NP-hard问题，因此，已有研究主要集中在问题的求解方法上。虽然MV模型十分直观地反映了投资组合管理中的两个重要目标，但是其缺陷也一直受到学术界的诟病。首先，MV模型对股票收益的度量需要前期消除长期趋势的股票价格，这就会导致价格共同趋势的信息丢失，并对样本数据有很强的敏感性。其次，MV模型仅使用两个统计量来描述投资组合的收益分布，这可能导致重要信息被忽略。为了解决第一个问题，Alexander等[1]提出了基于协整关系的增强型指数追踪模型，以股票价格代替收益作为衡量指标。Li等[2]将价格共同趋势加入到了优化模型中，并在增强型指数追踪问题中考虑到了最优化策略过程。然而，这些研究并不能解决第二个问题。

在本文中，我们提出将考虑整体资产收益分布的随机占优（Stochastic Dominance，SD）规则引入MV分析框架中，建立增强型指数投资组合模型。与MV模型不同，SD模型有以下优势：首先，SD不限制效用函数和投资收益分布的形式，而是从投资收益率的概率分布中衍生出的弱條件;其次，SD排序规则考虑了资产的整体收益分布，而不是仅仅考虑均值、方差和beta系数;第三，SD不是建立在像市场模型那样的线性收益产生过程的基础上。由于SD利用了“价格、概率和偏好”[3]，因此被认为是投资组合选择中的一个更合理的工具。但由于计算量大和计算困难等原因，SD模型一直未得到广泛应用。

为了克服SD的计算困难，本文采用边际条件下随机占优（Marginal Conditional Stochastic Dominance，MCSD）作为SD规则的替代。MCSD是Shalit等[4]提出的一种基于二阶随机占优（Second Stochastic Dominance，SSD）的资产优化选择方法。MCSD不需要对投资组合中所有资产的可能组合进行无限次的两两比较以获得有效的投资组合，而只考虑投资组合中资产权重的边际变化。也就是说，投资决策是在有限的、有条件的情况下做出的，因此不需要频繁地改变核心投资组合。为了便于计算，Shalit等[4]提出，MCSD可用于将单个资产或投资组合与市场投资组合进行比较。在这个意义上，MCSD比SSD更适合于增强型指数追踪，因为它可以测试设计的投资组合和市场指数之间的占优关系。具体而言，本文在MV优化框架内，首次提出增加MCSD规则的优化目标和约束条件。通过借鉴Belghitar等[5]提出的“总股票收益（total stock performance，TSP）”的概念以及Chow[6]提出的MCSD的统计检验，本文提出“占优程度”的评价方法，使得投资组合选择问题变成了最大化占优程度以及对超额收益和跟踪误差的考虑。另一方面，我们在模型中加入了MCSD的两层约束。通过对投资组合的MCSD统计分析，找到占优于基准指数的MCSD效率集（即在该集合中的投资组合均边际条件随机占优于基准指数），同时在MCSD效率集中找到占优该集合中所有其他投资组合的那个投资组合，以确定其为最优投资组合。在模型构建的基础上，本文使用多目标免疫算法进行模型的优化求解，并设计了模型转换方法，最后使用8组世界主要股票市场指数及其成份股的历史数据对模型及算法进行测算，证明了本文所提出模型的有效性。

二、边际条件随机占优理论

边际条件随机占优理论由Shalit等[4]于1994年提出，它给出了在资产选择过程中，所有风险规避的投资者用一个资产边际替代组合中的另一个资产的概率条件。在投资组合选择中，已有研究使用二阶随机占优来进行模型的构建。例如Roman等[7-8]提出了基于二阶随机占优的最优投资组合选择模型。此外，Roman等[9]将他们的方法扩展到增强型指数投资组合的选择中。但是，SSD只考虑了投资组合的概率分布，而MCSD不仅考虑了投资组合，也考虑了每一只资产的概率分布。也就是说，一旦投资者面临新的投资选择，他们只需要考虑是否将这个新的资产加入到投资组合中，或者考虑是否剔除已有投资组合中的某只资产，而不变动整个核心投资组合。关于该理论的具体描述可在已有相关研究[10-12]中找到。

对边际条件随机占优的测量实际上相当于对一项资产相对于另一项资产的完全概率分布的测量，若比较两个市场的MCSD关系，则需要对所有概率分布进行两两比较，因此实施起来比较困难。基于此，Shalit等[4]提出可以对单个资产与市场组合进行MCSD比较。其基本思想是，如果市场组合占优于某项成份资产，则减少对该项资产的持有，同时增加其他资产的持有可以改进投资绩效;相反，若某项成份资产战胜市场组合，则增加该项资产的持有同时减少其他资产的持有同样能够达到改进投资绩效的结果。为了便于统计计量，Chow[6]给出了MCSD的统计检验。

从上述规则可以看出，资产依据投资组合的分布条件性地进行了排序。基于此，可以很容易地将其扩展到增强型指数投资组合的构建中。我们将基准指数作为核心投资组合，那么候选投资组合可以看作是核心组合的一个边际组成部分，从而可以检验投资组合是否比基准指数表现更好（或表现更糟）。

三、问题描述与模型定义

Chow[6]统计量可以直观地告诉我们对于一个风险规避的投资者，某个投资组合的收益分布是否能够占优整个市场组合。如果将MCSD规则引入指数化投资组合，我们需要以下两个步骤：（1）找到占优于基准指数的MCSD效率集，在该集合中的投资组合均占优于基准指数;（2）在MCSD效率集中找到占优该集合中所有其他投资组合的那个投资组合，则该投资组合为最优的投资组合。但是，这在计算上却存在很大的困难。首先，步骤（1）要求我们在所有可能的投资组合中将其与基准指数进行两两比较;其次，步骤（2）要求在所有的MCSD有效的投资组合中进行两两比较。相较于SSD，MCSD的最大优势在于其简化了SSD中要求的无限次的比较，因此我们需要发挥它的这个特点。

为了避免在其中需要无限次地进行投资组合绩效的两两比较，本研究提出了“占优程度”的评价方法。因此，步骤（2）转化为在MCSD效率集中寻找拥有最高占优程度的投资组合。

根据Chow[6]检验法，指数收益Rt会按照升序排列并分成十个分位数。这十个分位数则作为累计概率P，为每一个MCSD关系测试得到10个统计量。令τt=F-1R（P），则每一个分位数的指数收益为τt。在前述MCSD规则加入指数投资组合的两个步骤中，步骤（1）对于最优模型的选择来说是一个强制性条件，因此在本研究的模型中处理为约束条件。根据Chow[6]对MCSD的统计检验方法，一个投资组合是占优投资组合必须满足下列约束：

其中，2.81是查表得到的在5%的显著性水平下，自由度为∞，系数为10的SMM渐进临界值，可在Stoline等[13]的研究中获得。

式（3）等同于这样的规则：“如果存在正显著的Zτt，同时没有Zτt小于2.81，那么这个投资组合占优于基准指数”[6]。步骤（2）考虑了“占优程度”。根据随机占优理论，占优意味着如果选择这个投资组合，那么投资者的效应将有所提高。因此，占优需要在投资组合中间进行两两比较。而由于没有普遍接受的基准，占优程度无从度量。但在MCSD中，我们可以度量这一指标，因为我们将投资组合以其基准指数的收益条件性地进行了排序。

式（4）是考慮了MCSD规则的目标函数。显然，当τt为第十分位数的数值时，τt将等于ER。由于考虑了收益的整体分布，MCSD规则为优化模型提供了更多的信息。

（二）模型定义

除了上述目标函数（4），基于MCSD的增强型指数投资模型中所包含的其他目标函数和约束条件还有：

其中，式（5）和（6）是收益风险优化下的目标函数。式（5）是投资组合的风险，在指数化投资中称为跟踪误差。这里我们使用了非对称的度量，即只最小化下方偏差，使其更适合增强型指数投资组合的要求。1/T表示每一个时间段对风险函数的影响是一致的。式（6）是收益函数，测量了投资组合的收益超过基准指数收益的程度。

式（7）到式（12）是模型的约束条件。其中，式（7）表示市场不允许卖空。在某些市场中，单只股票在投资组合中的权重有所限制。因此，我们使用ε和δ代表股票在投资组合中的投资下限和上限。式（9）表明我们的模型是一个自融资战略，即在整个投资周期没有现金的流入和流出。这里q0i代表初始投资组合中股票i（i=1，…，N）的数量。式（10）是交易成本约束。我们的模型假设交易成本的融资来自于独立于投资组合的账户。交易成本定义为η∑Ni=1pTi|qi-q0i|。式（11）和（12）是基于MCSD规则加入的两个约束条件。

四、算法设计

本文使用多目标免疫算法来求解上述优化模型。由于引入MCSD规则，使得模型在计算难度上有所增加，因此我们采取以下方法对模型进行转换。

（一）模型转换

在我们的模型中，MCSD规则包括一个目标函数和两个约束。其中，约束（11）和（12）与MCSD统计量（即Zτt值）的排序有关。而在现有相关研究[2，14]中提出的初始化过程和可行性排序技术都难以处理它们。因此，我们把这两个约束条件转化成如下两个目标函数：

转化后的模型并不是原始方程的等价方程，但是，我们认为这样的转化有如下几个优势：

（1）该模型更容易计算。这种转换使我们的模型与我们之前文章提出的模型具有相同数量的约束条件，这意味着可以使用此前研究中提出的一系列方法来处理约束条件，从而为该模型开发出一个合理的优化算法。

（2）对“占优程度”的定义是一个补充。正如论文第二部分描述的，我们将“占优程度”定义为Zτt的平均值。在统计理论中，平均值是中心趋势的度量。通过最大化Zτt的最大值与最小值，分散趋势也得到了控制。因此，我们的模型是在MCSD统计量Zτt的极值和均值中寻找拥有最大值的投资组合。

（3）简化了算法的复杂程度。通过上述转换，我们的模型不再需要对Z统计量进行显著性检验，因此在一定程度上简化了算法的复杂程度。（二）抗体和适应度函数

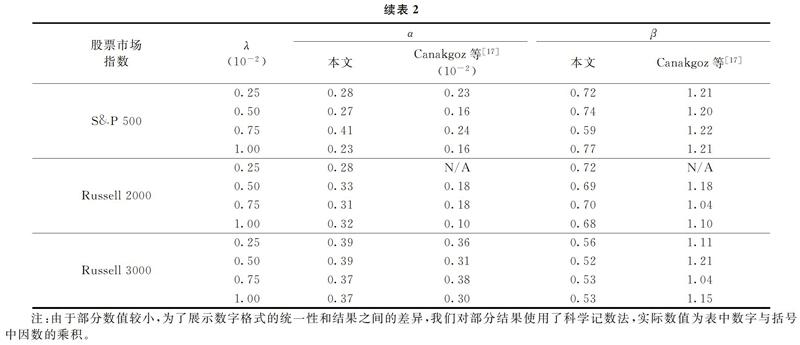
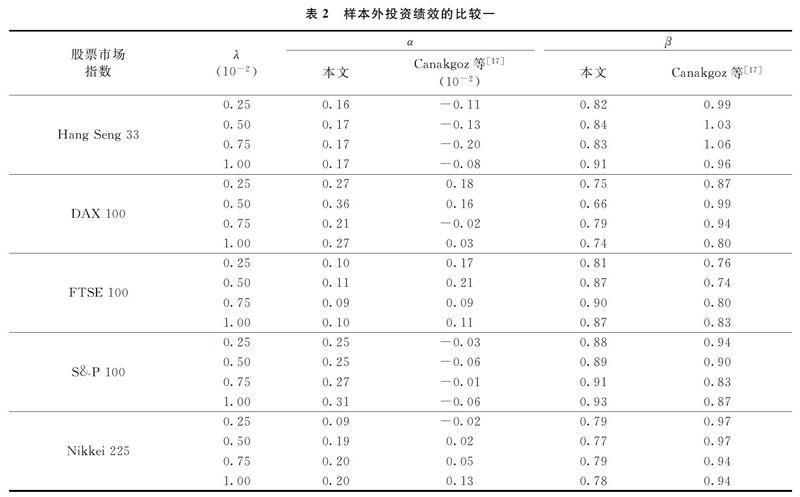
为了进一步显示本文模型的优越性，我们将模型的测试结果与已有研究进行了对比。这些已有研究均采用了与本研究相同的数据集，包括Canakgoz等[17]与Li等[14，2]的研究。其中，Canakgoz等[17]使用回归模型对结果进行了改变。为了使结果具有可比性，我们参考Canakgoz等[17]的做法，在样本外区间将投资组合的收益与其基准指数的收益进行了回归。而其他两个研究直接使用了与本文相同定义的跟踪误差和超额收益进行模型绩效的评判，因此我们将本文模型的样本外绩效与其进行了直接的对比。如表2所示，最小二乘回归参数α代表了投资组合的投资收益战胜基准指数的程度，α越大代表投资组合的绩效相对其基准指数越好。同时，如果投资组合完美复制了基准指数，那么α=0同时回归系数β=1。从表2可以看出，我们模型的α值均大于Canakgoz等[17]的结果，而模型的β值部分优于Canakgoz等[17]的结果。因此，我们可以认为，基于MCSD的投资组合的收益增强效果更好。

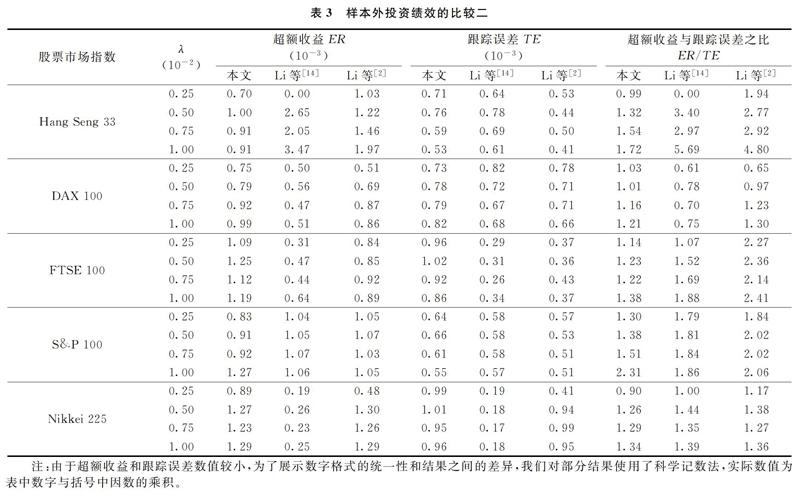
表3給出了我们的模型与其他两篇文献研究的结果比较。从中可见，在20个结果中，

我们的模型有14个结果优于Li等[14]的超额收益ER，有11个结果优于Li等[2]的超额收益ER。对三组超额收益与跟踪误差之比ER/TE分别进行两两T检验，结果发现，我们模型的超额收益与跟踪误差之比ER/TE与Li等[14]的超额收益与跟踪误差之比ER/TE之间没有显著差异（P值=0.215），但与Li等[2]的结果有显著差异（P值=0.006），我们的超额收益与跟踪误差之比ER/TE显著小于Li等[2]的结果。这说明我们的模型虽然增大了投资组合的超额收益，但是也相应增大了投资组合的跟踪误差。

为了更直观地展示本文的结果，我们给出了λ=0.0025时的模型效果（见图2）。由于篇幅所限，我们只展示了DAX100、FTSE100、S&P 500和Russell 2000四个数据集的结果。图2给出了在样本外区间内我们的模型及其相应的基准指数的走势。由于初始投资组合的价值设定与基准指数的价值相差较大，因此我们调整了投资组合的价值以使其与基准指数具有可比性。从中可以看出，基于MCSD的投资组合与基准指数具有相似的变化趋势，但基于MCSD的投资组合在样本外区间持续地战胜了基准指数的绩效。

六、结论

本文基于边际条件随机占优法则（MCSD）提出了增强型指数投资组合的模型及其优化算法。该模型建立在均值方差优化的框架内，但是结合了以MCSD为基础的约束条件和目标函数。其中，约束条件定义为MCSD效率，目标函数定义为MCSD统计量的均值优于基准指数的程度，即占优程度。因此，该模型一方面具备了MV模型的优点，如计算的便利性和直观性，另一方面，新加入的MCSD规则能够在优化过程中解决重要信息的遗漏问题。本文使用了一个多目标免疫进化算法对模型进行了求解，并使用了8个来自世界主要市场的指数及其成分股的历史数据对模型和算法进行了实证测算。结果表明，本文提出的模型和算法在逻辑上具有合理性，同时，MCSD规则的加入显著地提高了投资组合的投资绩效。与已有相关研究的结果相比，本文提出的模型在结果上也有一定的优越性。本文对随机占优规则加入投资组合的构建进行了一个初步的尝试，如何系统地将各种随机占优规则加入到投资组合模型的构建中，同时考虑多阶段的投资过程，将是今后的一个研究方向。

参考文献：

[1] Alexander C， Dimitriu A. Indexing and statistical arbitrage [J]. Journal of Portfolio Management， 2005， 31（2）： 50-63.

[2] Li Qian， Bao Liang. Enhanced index tracking with multiple time-scale analysis [J]. Economic Modelling， 2014， 39： 282-292.

[3] Lo A W. Three Ps of total risk management [J]. Financial Analysts Journal， 1999， 55（1）： 13-26.

[4] Shalit H S， YitzhakiS. Marginal conditional stochastic dominance [J]. Management Science， 1994， 40（5）： 670-684.

[5] Belghitar Y， Clark E， Kassimatis K. The prudential effect of strategic institutional ownership on stock performance [J]. International Review of Financial Analysis， 2011， 20（4）： 191-199.

[6] Chow K V. Marginal conditional stochastic dominance， statistical inference， and measuring portfolio performance [J]. Journal of Financial Research， 2001， 24（2）： 289-307.

[7] Roman D， Darby-Dowman K， Mitra G. Portfolio construction based on stochastic dominance and target return distributions [J]. Mathematical Programming， Series B， 2006， 8（2/3）： 541-569.

[8] Fabian C I， Mitra G， Roman D， et al. An enhanced model for portfolio choice with SSD criteria： a constructive approach [J]. Quantitative Finance， 2011， 11（10）： 1525-1534.

[9] Roman D， Mitra G， Zverovich V. Enhanced indexation based on second-order stochastic dominance [J]. European Journal of Operational Research. 2013， 228（1）： 273-281.

[10] 李倩， 張婧， 孙林岩， 等. 基于中国A股上市公司规模的投资方式的MCSD有效性检验 [J]. 系统工程， 2008（8）： 56-64.

[11] 李倩， 孙林岩， 张婧， 等. 中国A股市场价值成长效应的边际条件随机占优分析 [J]. 管理学报， 2010（3）： 423-427.

[12] 李倩. 上市公司的盈利信息能指导股票投资决策吗？——一个边际条件随机占优分析 [J]. 当代经济科学， 2013（3）： 115-123.

[13] Stoline M R， Ury H K. Tables of the studentized maximum modulus distribution and an application to multiple comparisons among means [J]. Technometrics， 1979， 21（1）： 87-93.

[14] Li Qian， Sun Linyan， Bao Liang. Enhanced index tracking based on multi-objective immune algorithm [J]. Expert Systems with Applications， 2011， 38（5）： 6101-6106.

[15] Gong Maoguo， Jiao Licheng， Du Haifeng， et al. Multiobjective immune algorithm with nondominated neighbor-based selection [J]. Evolutionary Computation， 2008， 16（2）： 225-255.

[16] Beasley J E， Meade N， Chang T J. An evolutionary heuristic for the index tracking problem [J]. European Journal of Operational Research， 2003， 148（3）： 621-643.

[17] Canakgoz N A， Beasley J E. Mixed-integer programming approaches for index tracking and enhanced indexation [J]. European Journal of Operational Research， 2009， 196： 384-399.

责任编辑、校对： 郑雅妮