例说一类中考常见题型——特殊三角形问题

沈伊昭

(福建省宁德市周宁县狮城中学 355400)

每年中考特殊的三角形都是老师们研究讨论的重点、热点.在复习中本人注意到一类与特殊三角形有关的问题，与同仁们一同探讨学习.

一、作图题

例1 已知坐标原点O和点A(2，2)，试在坐标轴上找到一点P，使△AOP为等腰三角形，写出满足条件的点P的坐标____.

分析 这是一道求作等腰三角形的开放性题目，比较容易丢答案.学生很容易作出一种如图2的情况，或者可以作出图3的情况.

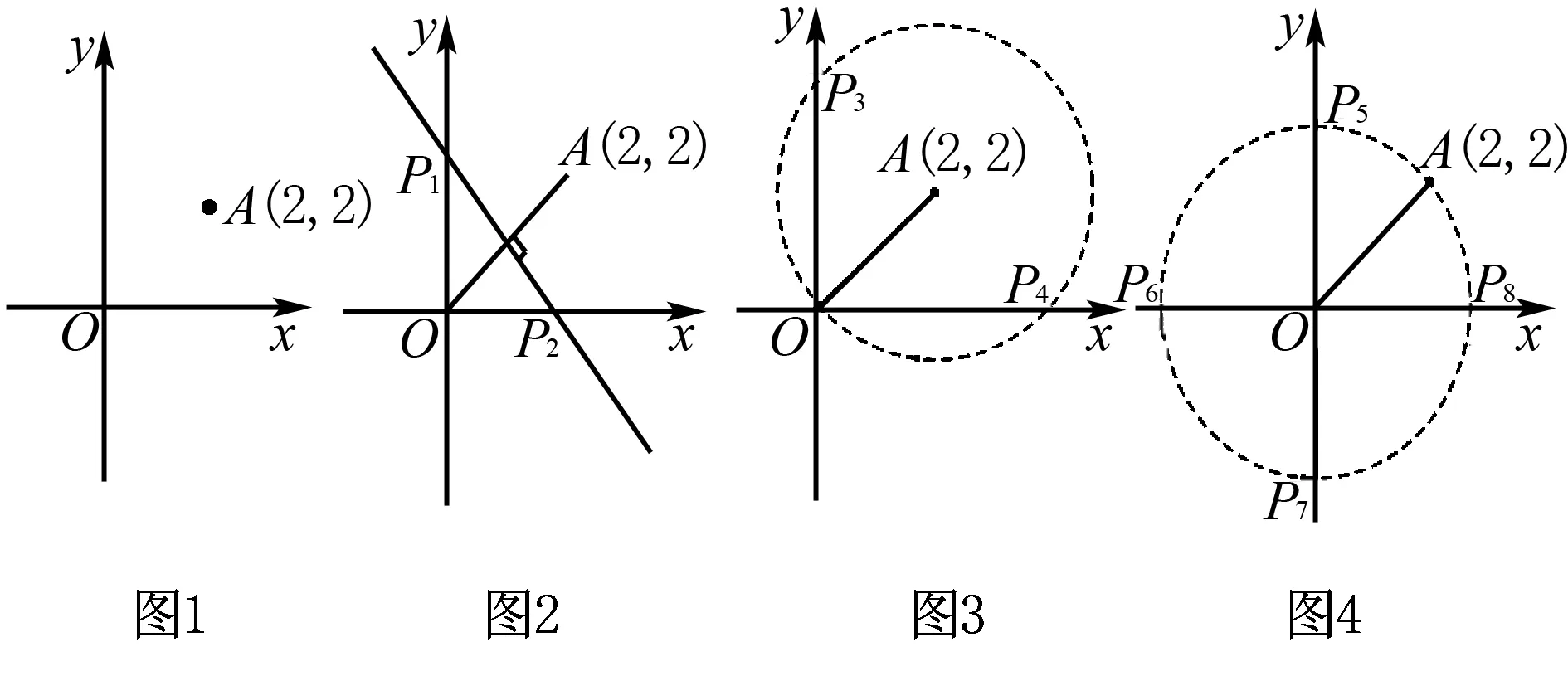
但受思维定势的影响，往往就无法继续作出其他种情况.要是能引导学生去思考第一种作法的本质特点：从定义出发作等腰三角形，要么考虑OA为底要么就考虑OA为腰，以OA为底就是连接OA，作OA的中垂线交坐标轴于点P1、P2(图2).以OA为腰就要考虑将点A当作顶角的点，还是把点O当作顶角的点问题了.若点A为顶角的点，根据AO=AP，以点A为圆心，AO长为半径作圆，交坐标轴于P3、P4(图3).同理点O为顶角的点，根据OA=OP，以点O为圆心，OA长为半径作圆，交坐标轴于P5、P6、P7、P8(图4).

二、与旋转相结合

例2 如图点O是等边△ABC内的一点，∠AOB=110°,∠BOC=α,将△BOC绕点C按顺时针方向旋转60°得到△COD，连接OD.

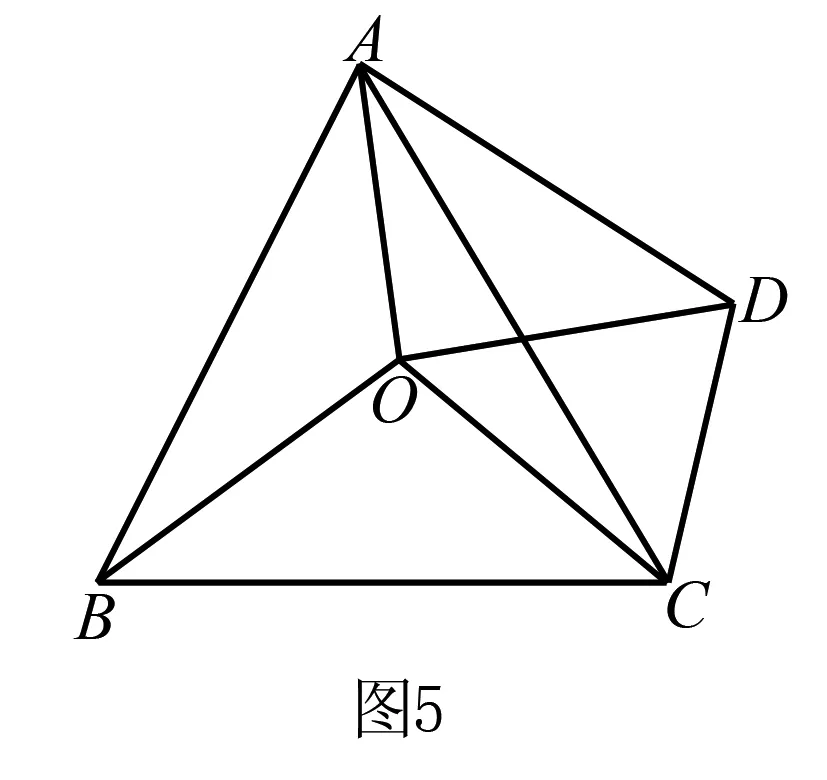
(1)求证：△COD是等边三角形;

(2)当α=150°时,试判断△AOD的形状,并说明理由

(3)探究：当α为多少度时，△AOD是等腰三角形？

分析 (1)(2)较为简单，这里不多说了.我们看看(3)，根据我们例1判断等腰三角形的方法(边或角相等)，依题意本题应该从角度出发，△AOD是等腰三角形有三种： (1)∠ADO=∠AOD,(2)∠AOD=∠OAD,(3)∠OAD=∠ADO.但学生往往还是只得到一种而丢掉另两种,这仍属于思维单一，发散不够造成的.那么如何求解呢？可以由边的关系得到角的等量关系，因此先要用角α把△AOD的三个角表示出来：

∠AOD=360°-∠AOB-∠BOC-∠DOC=360°-110°-α-60°=190°-α,∠OAD=180°-∠AOD-∠ADO=180°-(190°-α)-(α-60°)=50°,∠ADO=∠ADC-∠ODC=∠BOC-∠ODC=α-60°.

所以，若∠AOD=∠ADO,则α=125°；若∠OAD=∠ADO,则α=110°;若∠OAD=∠AOD,则α=140°.

综上所述：α=125°或110°或140°.

三、与抛物线相结合

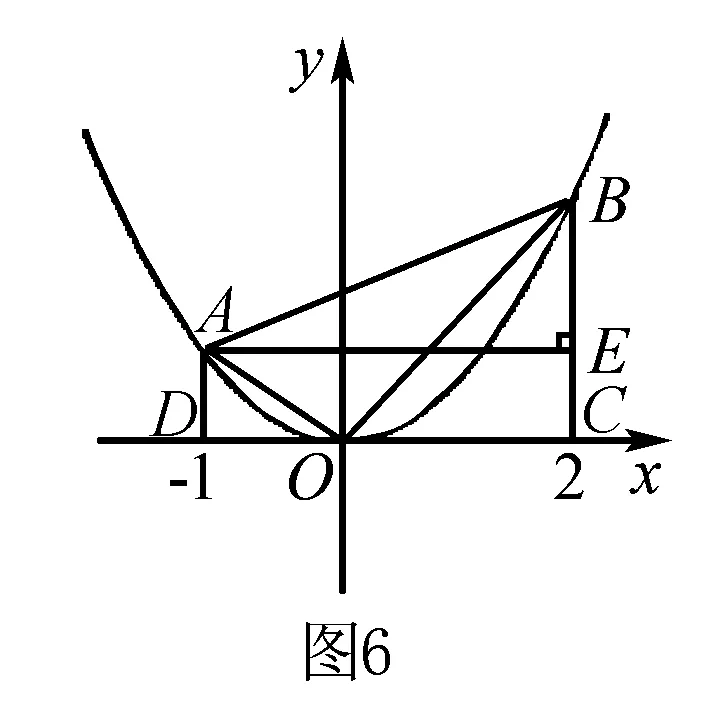
例3 已知抛物线y=ax2(a>0)上有两点A、B其横坐标分别为-1，2，试探求a的取值情况，△AOB可能是直角三角形吗？若不能，说明理由；是直角三角形，请写出探求过程.

分析 本题抛物线未定，所以△AOB的形状也随之改变.看似没有头绪，其实奥妙深藏在△AOB是直角三角形中，△AOB是直角三角形必定有一个角等于90°，这样我们就可以如例2一样的方法来求解，先求得三边AB，AO，BO的长度(用a的代数式表示)，设A(-1，a),B(2，4a),过点A作AE⊥BC.

∴AO2=DO2+AD2=1+a2,BO2=OC2+BC2=16a2+4,AB2=BE2+AE2=9a2+9.进而根据勾股定理的逆定理

讨论：若∠AOB=90°或∠BAO=90°或∠OBA=90°,分三种情况求a的值.

从以上例子可以看出，在中考中有关特殊三角形的问题对学生的能力要求是比较高的.学生在求解这类问题常见的问题：(1)无法下手，(2)对定义的理解不够，解题缺乏方向性，(3)思维发散不够，容易漏解，(4)缺乏边与角之间转换的技能．所以我们只要找到问题的关健，就有办法对症下药，引导学生正确思维，通过横向对比，触类旁通，多加训练，必会事半功倍，起到很好的效果.