概率的特点与求解策略

王 晖

(安徽省灵璧县黄湾中学 234213)

一、概率题的特点

1. 考查的类型

从近年来各地的中考试题来看，有关概率的试题主要考查的知识点：随机事件，频率与概率的关系，通过计算预测随机事件的概率，以及概率的应用.

2. 试题特点

(1)概率试题的题量大致为1～2题，约占全卷的10%左右，试题难度多为容易题或中等题.

(2)概率试题的背景，大多贴近日常生活实际，让人感到亲切、真实，充分地体现了数学的人文教育精神.

(3)概率试题具有一定的应用性和趣味性，充分体现了在玩乐中学习数学知识这一理念.

二、考题类型举例分析

1. 判断事件的可能性

例1 4个红球、3个白球、2个黑球放入一个不透明的袋子里，从中摸出8个球，恰好红球、白球、黑球都能摸到，这件事情( ).

A. 可能发生 B. 不可能发生

C. 很可能发生 D. 必然发生

解析 因为三种球共有9个，而且没有一种球有8个，也没有2种球的和为8个，所以若摸出8个球，三种球都能摸到是必然事件.应选D.

例2 (2018沈阳)下列事件中，是必然事件的是( ).

A. 任意买一张电影票，座位号是2的倍数

B. 13人中至少有两个人生肖相同

C. 车辆随机到达一个路口，遇到红灯

D. 明天一定会下雨

解析 座位号有奇数和偶数，故“任意买一张电影票，座位号是2的倍数”是随机事件；一共12生肖，故“13人中至少有两人生肖相同”是必然事件；车辆随机到达一个路口，可能遇到红灯，也可能遇到绿灯，还可能遇到黄灯，故C中的事件是随机事件；明天可能下雨，也可能下雨，则选项D中的事件是随机事件.故应选B.

例3 (2018襄阳)下列语句所描述的事件是随机事件的是( ).

A. 任意画一个四边形，其内角和为180°

B. 经过任意两点画一条直线

C. 任意画一个菱形，是中心对称图形

D. 过平面内任意三点画一个圆

解析 任意一个四边形的内角和都为360°，故选项A中的事件是不可能事件；两点确定一条直线，故选项B中的事件是必然事件；菱形都是中心对称图形，故选项C中的事件是必然事件；即A、B、C中的事件都是确定事件.不在同一条直线上的三点确定一个圆，而在同一条直线上的三点无法确定一个圆，故选项D中的事件是随机事件.所以应选D.

2. 研究频率与概率的关系

概率被我们用来表示一个事件发生的可能性的大小，对事件可能性的大小的感觉通常来自观察这个事件发生频率，即该事件实际发生的次数与试验总次数的比值.但是在相同的条件下，在进行大量重复试验后，事件出现的频率会逐渐稳定，稳定后的频率可以作为概率的估计值.

例4 为了调查宿州市今年有多少名考生参加中考，小聪从全市所有家庭中抽查了200个家庭，发现其中10个家庭有子女参加中考.

(1)本次抽查的200个家庭中，有子女参加中考的频率是多少？

(2)如果你随机调查一个家庭，估计家庭有子女参加中考的概率是多少？

(3)已知宿州市约有1.3×106个家庭，假设有子女参加中考的每个家庭中只有一名考生，请你估计今年全市有多少名考生参加中考？

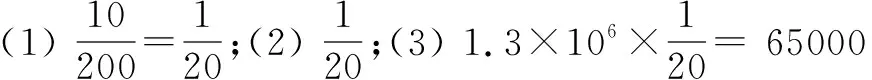
3. 通过计算预测随机事件发生的概率

(1) 通过计数计算概率

例5 若从一副扑克牌中取出的两组牌，分别是黑桃1、2、3、4和方块1、2、3、4、，将它们背面朝上，分别重新洗牌后，从两组牌中各摸出一张，那么摸出的两张牌的牌面的数字之和等于5的概率是多少？请你用列举法(列表或画树状图)加以分析说明.

解析 可用列表法列出所有的可能得到的牌面数字之和：

黑桃1黑桃2黑桃3黑桃4方块11+1=22+1=33+1=44+1=5方块21+2=32+2=43+2=54+2=6方块31+3=42+3=53+3=64+3=7方块41+4=52+4=63+4=74+4=8

(2)通过长度、面积、体积公式求概率

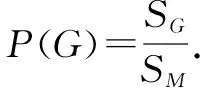
例6 某商场进行有奖促销活动，活动规则：购买500元商品就可以获得一次转盘的机会(转盘分为5个扇形区域，分别是特奖彩电一台，一等奖自行车一辆，二等奖圆珠笔一只，三等奖卡通画一张及不获奖)转盘指针停在哪个获奖区域就可以获得该区域相应等级奖品一件.商场工作人员在制作转盘时，将获奖扇形区域圆心角分配如下表：

奖次特等奖一等奖二等奖三等奖圆心角1°10°30°90°

①获得圆珠笔的概率是多少？

②如果不用转盘，请设计一种等效实验方案(要写清楚替代工具和实验细则).

②可采用“抓阄”或“抽签”的方法代替.规则如下：在一个不透明的箱子里放入360个除标号不同外，其它都一样的乒乓球，其中一个标“特”，10个标“一”，30个标“二”，90个标“三”，其余的不标数字，摸出标有哪个奖次的乒乓球，则获奖相应等次的奖品.

4.随机事件概率的应用

了解事件发生的概率，有利于决策者对问题的解决作出合理的选择.解决这类问题的一般方法是：从实际问题中抽象出概率的模型计算概率，然后根据概率的大小作出合理的决策.

例7 有一个抛两面硬币的游戏，规则是：若出现两个正面，则甲赢；若出现一正一反，则乙赢；若出现两个反面，则甲、乙都不赢.

(1)这个游戏是否公平？请说明理由.

(2)如果你认为这个游戏不公平，那么请你改变游戏规则，设计一个公平的游戏；如果你认为这个游戏公平，那么请你改变游戏规则，设计一个不公平的游戏.

(2)游戏规则一：若出现两个相同面，则甲赢；若出现一正一反，则乙赢；

游戏规则二：若出现两个正面，则甲赢；若出现两个反面，则乙赢；若出现一正一反，则甲、乙都不赢.

例8 (2018黄冈)在-4,-2,1,2四个数中，随机取两个数分别作为函数y=ax2+bx+1中a,b的值，则该二次函数图象恰好经过第一、二、四象限的概率为____.

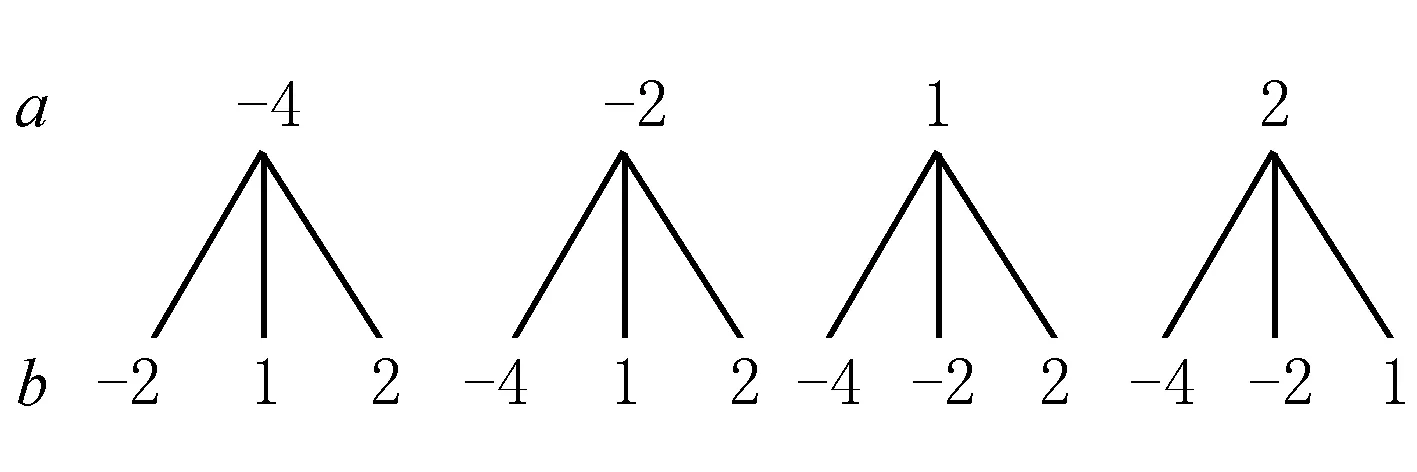
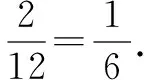
点评 二次函数的图象恰好经过第一、二、四象限需满足：(1)开口向上；(2)与x轴有两个交点；(3)与y轴交于正半轴；(4)对称轴在y轴右侧.