初中数学易错题的产生及提前干预的策略研究
吴国凤
(浙江省杭州市萧山区金山初中 311200)
一、课题的提出
泰戈尔哲理诗中有一句名言:“当你把所有的错误都关在门外,真理也就被拒绝了.”错误本身就是一种学习资源.研究表明,只要积极正视自身的错误,并进行行之有效的提前干预,就能够收到事半功倍的效果.
在数学学习中,错题是不可避免的,它能直接反映学生的掌握情况,错题的层次可以分基础型和能力提高型.有一类错题不复杂,但是学生很容易出错或经常出错,我们称之为易错题.有些易错题教师多次讲解,但效果不明显.教师在教学中通过提取学生的数学作业、练习或考试卷中出现的错误,对错题进行归类整理,对题目的层次进行分类,找出易错题,对这些题目进行提前的干预,减少学生犯错的机会.
二、课题研究的目的与意义
1.课题研究的目的
(1)帮助教师全面了解初中生易错的知识点及题目类型.在教学中注意采取合理的策略,避免某类错误的发生.
(2)帮助学生了解自己可能出现的错误,从而注意防范;出现问题后,从哪些方面加以弥补.帮助学生解决学习中的知识漏洞,提高学习的效果.
2.课题研究的意义
教师及时发现学生学习中的易错点,并进行提前干预,让学生减少类似错误的发生.指导学生学会归纳、梳理,抓住知识的本质,提高学习的有效性.
三、课题概念的界定
1.易错题:有两层涵义:一是大多数学生都会发生错误的题目;二是一个学生在同类问题多次犯的错误.
2.提前干预:对某事物提前采取措施,以减少错误的发生,这里我们指的是对学生都容易犯的错误提前采取措施,通过正确的引导减少错误的发生.
四、课题研究的内容和策略
1.易错题产生的原因
(一)从数学知识看
(1)小学数学知识的干扰
进入初中后,出现了负数、用字母表示数、函数的知识等,小学中的一些概念已经不适用,由于思维定势,会造成易错题的形成.
例如,七上《2.2有理数的减法(1)》新课时“A地海拔高度是-10米,B地海拔高度是30米,A地地势与B地地势相差几米?”不少同学填了20米.错误的产生都是因为小学知识的干扰造成,忽视负数的实际意义.
(2)初中基础性知识的掌握不到位
①对概念性知识的理解不清晰
学生忽视概念的学习和理解,导致知识体系不扎实、不完善.例如,在学习一元一次方程的定义后,完成题目:已知方程(1-k)x3-2│k│-2k=4是一元一次方程,试确定k的值并解这个一元一次方程.学生的错解是3-2│k│=1,k=±1.错误的原因是忽视了x的系数不能为零的条件.
②对应用性知识的理解不正确
学生对法则,定理、公式等知识的掌握不扎实,在应用中引起错误的产生.例如,在学习有理数的减法法则时,1-2中2前面的“-”是减号,紧接着学习《2.2有理数的减法(2)》时,课本强调把1-2看成+1与-2之和,“-”又成了负号.学生对2前面的符号产生困扰.错误是由于学生不理解“一个数字前面有两个符号,一个是运算符号:加减号,一个是性质符号:正负号”.
③对表述性知识的理解不透彻
学生学习表述性知识时,产生一知半解的想象.例如,在学习七上《平行线》时,判断下列说法正确的( )个:①经过两点有且只有一条直线;②两条直线不平行必相交;③过一点有且只有一条直线与已知直线垂直;④过一点有且只有一条直线与与已知直线平行.很多学生填3个或4个.错误的原因就是因为学生对平行线的定义和平行公理等表述性知识理解不透彻,忽略了概念中的“在同一平面内”和“在直线外”.
(二)从学习方法看
(1)学生学习新知识时理解含糊,不弄清知识的来龙去脉,只知其然不知其所以然.例如,学习七上《2.7近似数》时,由四舍五入得到的近似数83.50,精确到____位,它表示大于或等于____,小于____的数.1.2万精确到____位.这个易错的原因就是学生没有理解精确度的由来,只是记了例题的结果.
(2)学生在解题过程中,重结果,轻过程,急于求成,对概念、法则、公式、定理的应用一知半解.例如,在学习八上《2.5逆命题和逆定理》角平分线性质定理的逆定理时,完成题目:如图(1)所示,计划修建超市,要求超市到三条公路距离相等.问可供选择的地方有多少处?你在图中画出来.学生的错解是如图(2),只有一处.而遗忘了外角的角平分线的交点有3处符合角平分线性质定理的逆定理.
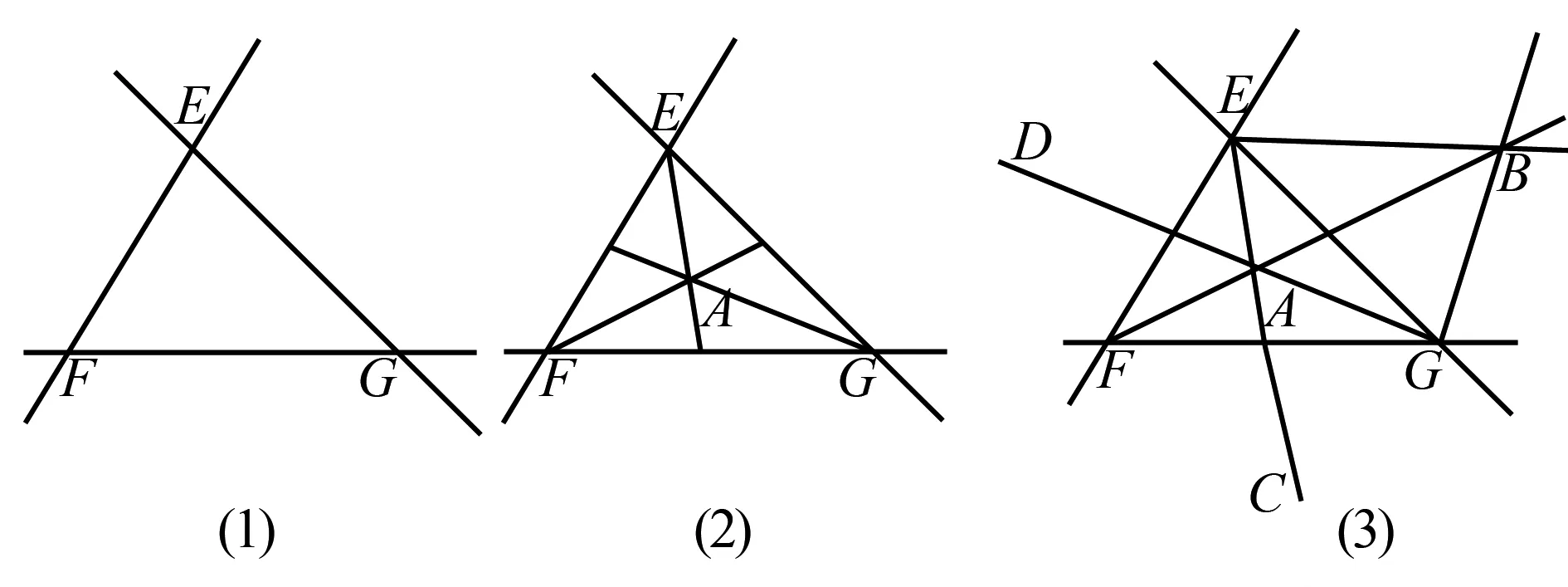
(3)学生对基础知识的迁移不够,学习过于死板,思维不灵活.例如,学习八上《1.3证明(2)》的三角形外角性质时,完成下题:已知如图AB∥CD,分别求出下面四个图形中∠APC与∠PAB,∠PCD的关系.在实际操作中,学生不会添辅助线,不会应用三角形的外角性质和平行线的性质.
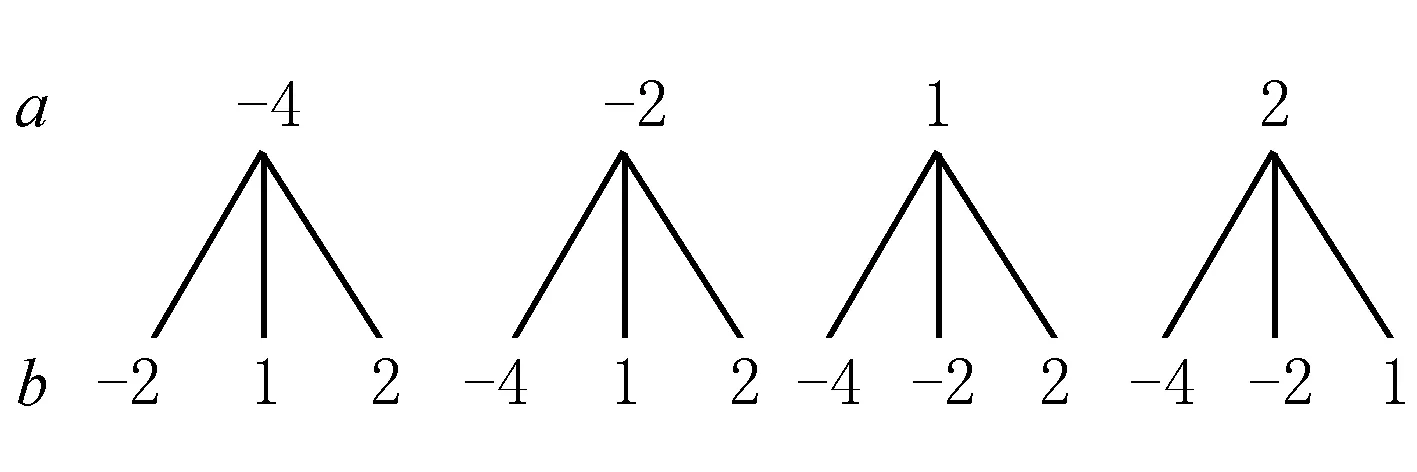
(三)从学习习惯看
(1)学习专注度不够,计算类错误频繁出现.
学生计算错误都以粗心、不仔细为借口,对自己的错误不重视.例如,在学习有理数加减时,计算-6-4+8时,会产生错解:-6-4+8=-2+8=6.出现类似错误时,学生轻描淡写,没有去克服错误的发生.
(2)学生内心急于求成,审题类错误屡见不鲜.
审题失误的原因是多方面的:一是急躁心理,匆忙审题,碰到阅读量大的题目就心烦意乱,匆匆落笔;二是求快心理,还没有“看清”“看全”题目就开始动手做题,有些条件给出比较隐蔽,没有挖掘加工.三、思维定势,看到熟悉的题目就想当然,甚至看错简单的条件.例如,已知直角三角形的两边长为3,4,则第三边长为多少.很多学生就只填了5.错误的原因就是学生没有仔细审题,习惯性思维3,4,5勾股数,而忽视了题中没有指明直角边与斜边.
2.提前干预易错题的策略
(一)课前准备要有预见性,对易错题进行提前预测
(1)精心设计教案,准备多种预设.在新授课中,教师要预设到学生学习过程中可能产生的错误,在讲解时有意识地指出并加以强调,从而有效地减少错误的发生.讲解要重视学生先入为主的现象,让学生在第一次接触新知识时就能清晰地掌握知识,特别是数学基础薄弱的学生,教师要给予学生正确的引导,通过一个个预设,让学生明白数学知识的严密性,设计问题一层一层的深入.
例如,以七上《1.2数轴》中数轴概念教学片断的设计为例:
步骤一:
1.每个学生发一个温度计,教师用一次性筷子提前制作一支仿真的温度计.
2.老师引导学生观察温度计后,追问:
(1)温度计是否有刻度(包括零刻度线)?
(2)刻度是否均匀?
(3)刻度标法顺序是怎样的?
(4)温度计上的刻度排列是否有方向性?
教师小结:把这支温度计抽象成一条向两方无限伸展的数轴,引出课题——数轴.
步骤二:
1.师生共同仿照温度计画一条数轴.(教师板演)
2.教师引导学生学会画数轴的基本步骤.
第一步:画直线定原点;
第二步:规定从原点向右的方向为正(左边为负方向);
第三步:选择适当的长度为单位长度(据情况而定);
第四步:拿出温度计,由学生观察温度计的结构和数轴的结构是否有共同之处.
请学生对比思考:原点相当于什么;正方向与什么一致;单位长度又是什么?
3.请学生小结数轴三要素(原点、正方向、单位长度).最后学生练习画数轴.
这样的数轴概念的教学设计让学生对知识的理解很清晰,教师可以提前干预学生画数轴时容易出现缺少三要素的情况,促使学生真正理解数轴的概念.
(2)设计学生的预习案,让学生提前预习,完成预习内容.教师观察学生预习完成的内容,了解学生思维上容易出错之处,在课堂上及时纠正错误,提前干预错误的发生.
例如,以七下《5.5分式方程(1)》预习案中的完成内容为例,
问题一:分式方程的概念.
1.某电话公司调低了话费标准,每分费用降低了25%,因此按原收费标准6元话费的通话时间,在新收费标准下可多通话5分钟.问前后两种收费标准分别是多少?回答下列问题:(1)题中主要等量____;(2)设原来的收费标准是x元/分,可列怎样的方程?____;(3)该方程与我们已学过的一元一次方程有什么不同?____.
2.归纳小结:分式方程的概念:____.
3.判断下列各式哪个是分式方程.
问题二:解分式方程
1.找出下列各组分式的最简公分母:


小结:解分式方程的主要思想是将分式方程化为____方程,方法是方程两边同乘以____,去掉分母.
学生通过完成预习案内容,对于分式方程的概念和增根的定义有清楚的理解,在预习案上很多学生写了以下疑惑:①分式方程必须要写出验根过程吗?②分式方程在验根时把解代入方程的两边还是直接代入最简公分母检验?③分式方程在什么情况下无解?教师通过批改预习内容对学生学习中的错误有了提前干预,在课堂讲解中对易错的地方有了重点的讲解.
(二)课内讲解要有针对性,对易错题进行现场跟进
在教学中不能过分强调教师的主导作用,教师要让学生踊跃发言,以便教师及时发现学生的易错题,现场跟进,争取在课堂练习中第一次出现错误的时候,在第一现场及时跟进,通过一定的干预措施,帮助学生及时纠正错误.
(1)准备课前复习的内容.采用竞赛活动、全班小测试、小组互考等形式,了解学生对知识的掌握程度,对遗忘及生疏的知识进行适当的练习回顾.
例如,在学习七上《1.3绝对值》时,在课前安排全班小测:①在数轴上,原点及原点左边的点所表示的数是____;②数轴上表示5和-5的点离开原点的距离是____,但它们分别____;③最小的正整数是____,最小的非负数是____,最大的非正数是____;④与原点距离为3.5个单位长度的点所表示的数是____.
(2)指导学生掌握有效的解题方法.在解题时,运用解题四步曲:审、思、解、查.在审题过程中要逐字逐句地读,审三遍的题,圈画题中的重要条件、重要语句,边阅读边分辨出已知量和待求量,凡是能画草图的题,应该边审题边作图,解完题后要检验.
(3)在课堂上及时反馈易错点.教师把当堂练习通过投影,让学生判断正误,并改正错误.教师要从不同角度思考问题的本质,鼓励学生多角度、多方位审视自己出现的错误,对学生的易错题进行正确诱导.
例如,学习八上《1.5三角形全等的判定(2)》时,学生会出现了“SSA”的情况,教师要提前干预错误的发生就提出一个问题:如果两个三角形有两边和一个角对应相等,那么这样的两个三角形一定全等吗?教师利用实例反馈,发现其中一个三角形的对应角不是两条边的夹角时两个三角形不全等(如图4).这样一来,“SAS”定理必须是两边的夹角,学生就避免“SSA”的出现.

(4)做好课堂笔记.课堂上要求学生人手有一本笔记,记入一些定理、法则的剖析,重点记入一些易错题,教师提醒学生把需要的内容记入到本子上,周末进行错题的分类整理.
例如,讲评七下《因式分解》的全效作业本的本章复习课时,学生所做的课堂笔记.
(三)课后讲评要有归纳总结,对易错题进行反思
(1)教师每天及时讲评作业中的易错题.总结出典型的错误,加以评述,并对易错题进行教学反思,进行适当的复习与总结,使学生再经历一次尝试与修正的过程.
(2)学生准备“易错题本”.学生在作业中答错易错题,一般来说,自己是意识不到的,因此让学生准备一个“易错题本”.第一部分记题目,第二部分记从审题、知识再现的准确性和解答过程的规范性三方面分析错误原因,如遗憾之错:就是分明会做,反而做错了的题,比如“审题之错”、“计算之错”、“抄写之错”、“表达之错”等,第三部分提出纠正方法和注意事项及正确的解答,再次做错的题则需要第三次做,每周做一个汇总,减少再犯错的概率,为有效干预易错题打下基础.“错题集”是自身错误的系统汇总,有助于知识的查漏补缺.
(3)教师准备一个“易错题集”.摘抄以前的学生所犯的错误.在教学过程中易错题原题重现,将以前易错的范例在课堂上展示,请学生挑错.学生对第一次接触的新知识的印象比较深刻,这样的练习可以预防或者减少这类型题目在课后的错误率.深入分析学生出现“错题”与自己的“教法”及学生的“学法”不当或不足的关系,学生该会不会的原因,适当进行提前干预,减少易错题的产生.
五、回顾与反思
在学习中,错误是难免的,关键是如何减少错误的发生,避免一错再错的现象.学生通过建立错题本可以随时提醒自己曾经出现的错误,要从易错题的错解中吸取教训,很好地提高了学生学习的效率.教师在教学实践中对易错题进行整理,把每一个知识点落实到位,有效控制易错题的出错率,使学生轻松愉快的学习数学.在课堂教学中,教师学会现场跟进,通过一定的干预措施,减少了易错题的发生.教师用发展的眼光看待学生的错误,尽量留给学生更多自我发现的时间和空间,给予学生主动改正错误的机会,使“错误”成为学生前进的动力.要利用好错题资源,让“错误”美丽起来.
无论是学生还是教师,面对错题,我们要正确对待.吃一堑,长一智,反思错题的原因,培养数学思维的良好习惯,优化逻辑思维品质.在数学学习中,不仅要及时纠正错误,反思错题,更要对教学中的典型例题和习题进行解题后的反思,优化现有的认识,提高自身的认知水平.教师要回顾过去的教学,认知即将发生的“错题”.在“出错”和“改错”的过程中,让数学课堂更鲜活,让数学教学更美丽.

