基于核心素养背景下初中几何最值问题的解题方法

蒋 雁

(广东省韶关市广东北江实验学校 512000)

一、运用转化思想―将问题转化成基本的最短路径模型

在运用转化思想构建最值问题时，一般会用到平移变换、抽对称变换以及旋转变换.平移变换更多的是通过平移线段来构造平行四边形，借助对边平行且相等来找到相对应的最短线段，从而解决问题求得最值.轴对称变换更多的是利用垂线段最短来解决问题，一般我们可以借助全等三角形、勾股定理以及相似三角形等来确定最值从而求出最小值.接下来我对旋转变换作进一步分析：

例如：已知P是锐角三角形ABC内的一个点，且使PA+PB+PC最小，试确定点P的位置，并证明你的结论.

由于题干只有文字信息，而对于几何图形必须通过图形信息去挖掘题目信息，因此，我们先根据题干信息作出如下解析图:

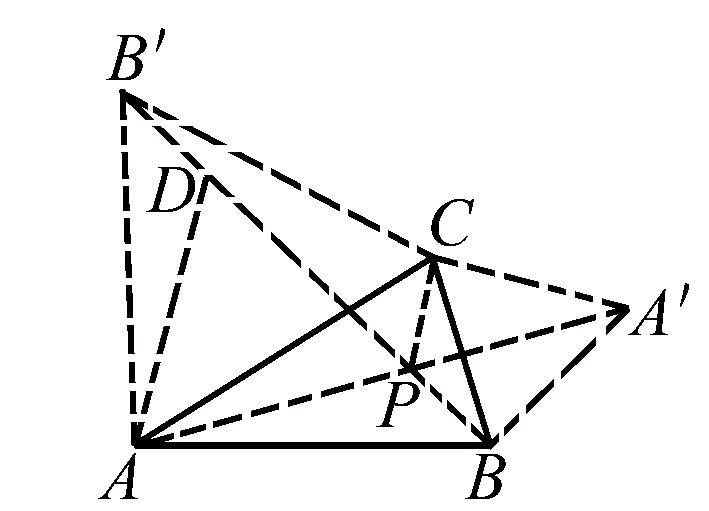
首先画出三角形ABC，接着以AC为三角形的一边向外作等边三角形ACB′，再以BC为三角形的一边向外作等边三角形BCA′.连接BB′以及AA′，此时BB′和AA′相交于一点P，而这一点P就是我们所要求的.

接下来证明PA+PB+PC=PD+PB+DB′是一个定值.由于△ACB′和△BCA′是等边三角形，因此得出结论：CA′=CB，AC=B′C，∠ACA′=∠BCB′，因此△ACA′全等于△B′CB.又因为∠B′BC=∠AA′C，所以得到∠BPA′=∠BCA′=60°，所以∠APB′=∠BPA′=60°.此时，在PB′上截取PD=AP，将AD、CP连接.由PD=AP，∠APB′=60°，得出△APD为等边三角形.又由AP=AD，AC=AB′，∠DAB′=∠PAC，得到△PAC全等于△DAB′，于是得到结论线段CP=B′D.从而知道PA+PB+PC=PD+PB+DB′是一个定值 .

然后需要证明PA+PB+PC为最小值，在△ABC的内部任意取一点M，如右图所示，此点M和点P不相同，将MA、MB以及MC连接起来，此时构成了△AMC，将△AMC以图中的A点为中心，逆时针旋转60°，得到一个新的三角形AGB′.在旋转的过程中，我们不难得到AC=AB′，AM=AG，MC=GB′，此时可以得出△AGM是一个等边三角形，由此推出MA=MG.由此，我们可以得到MA+MB+MC=MG+MB+B′G=BM+MG+GB′>BB′.综上所述，我们分析出点P到三角形三个顶点A、B、C的距离之和最短.

在这道题目中，利用三角形AMC的旋转变换将一组“Y”字型的线段巧妙地转成了两个定点之间的线段，再通过“两点之间线段最短”这一理论基础轻松地证明出P到三角形三个顶点A、B、C的距离之和最短.在教学过程中，对于这类求最值的稍复杂题型，是需要作多条辅助线的，这对学生的能力要求就比较高.在做这一类题目时，首先教师应引入一些简单图形的辅助线作法，培养学生作辅助线的意识，同时也训练了学生的动手能力.其次还应该将作辅助线的题目进行分类，让学生在脑海里形成清晰的概念，以便拿到相应的题作出相应的图，从而提高学生的解题效率.

二、运用模型思想―建立方程、函数模型

在解决最值问题时，还有一个常用的方法就是运用模型思想，也就是建立模型，在建立模型时，我们通常会用到方程、函数等的思想，利用均值不等式的计算方法.

例如：已知△XYZ是一个等腰直角三角形，其中直角边的边长是1，∠Z=90°.△XYZ的三个顶点分别在等腰三角形ABC的三边上，其中∠C=90°，求△ABC直角边长的最大值.

此题只说明了△XYZ的三个顶点分别在等腰三角形ABC的三边上，并没有说明△XYZ的三个顶点对应在△ABC的哪条边上，所以此时的答案就不唯一了，我们需要进行分类讨论.

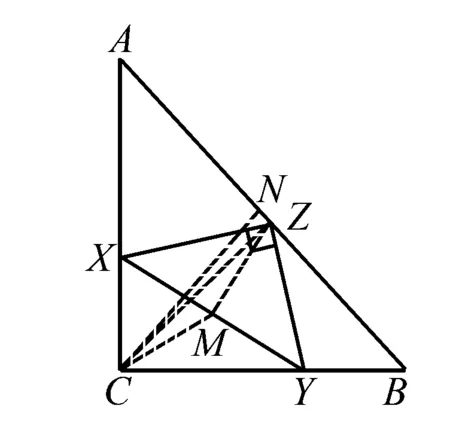
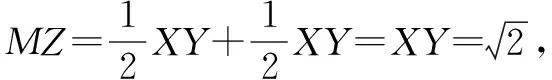
第二种情况：假如△XYZ的顶点Z在△ABC的直角边上，在这里我们假设Z点在CA上，此时过点Y作YH⊥CA于点H，在这里令CX=x,CZ=y.我们可以知道以下三个条件：ZY=ZX，∠XZC=∠ZYH，∠YHZ=∠XCZ=90°，因此△ZYH全等于△XZC，那么HZ=CX=x,HY=CZ=y，从而进一步可以得到△AHY是等腰直角三角形，于是得出AH=y.

总而言之，在初中数学的教学过程中，核心素养的应用与发展是学生发展的重要途径之一.因此，教师在数学课堂中，必须围绕核心素养来展开自己的教学，在教学过程中，教师应多设置情境教学来提高学生的学习兴趣、多设置操作环节训练学生的动手能力等等，总之，一切的目的都是提高学生的学习能力以及综合发展能力.