基于SVM的多项式循环程序秩函数生成*

李 轶, 蔡天训, 樊建峰,3, 吴文渊, 冯 勇

1(中国科学院 重庆绿色智能技术研究院 自动推理与认知重庆市重点实验室,重庆 400714)

2(萨基姆通讯(深圳)有限公司,广东 深圳 518000)

3(中国科学院大学 计算机科学与技术学院,北京 100093)

循环程序的终止性分析是程序验证的一个重要研究分支.在现代程序设计中,几乎所有的程序都会含有循环.然而,即使是简单的循环程序,也很容易出错.循环中的很多错误往往需要执行多次或在某些特定情况下才能被发现.因此,确保循环程序是可终止的是保障软件能够可靠运行的一个必要条件.尽管程序终止性问题早已被证明是一个不可判定问题[1,2].但是人们发现,具有某些特征的循环程序的终止性是可判定的.如:Tiwari在2004年证明了一类线性循环程序在实数域上的终止性是可判定[3].这类程序的终止性在文献[4-7]中被重新考虑.此外,Zhan等人在文献[8]中考虑了循环条件为等式的多项式程序的终止性问题,并给出了该类程序可终止和不可终止的充分判准.在文献[9]中,Zhang等人建立了针对程序终止性验证的高级自动机算法.在循环非终止研究方面,Zhang给出了一种能够检测出简单循环中出现死循环的充分条件[10].针对确定型线性赋值循环程序,Leike等人在文献[11]中给出了GNTA条件去探测这类循环的不可终止性.

秩函数法是证明循环程序可终止性的主要方法.给定一个循环程序,倘若它的秩函数被找到,则表明该循环是终止的.为计算秩函数方便起见,人们往往计算多项式型的秩函数.根据多项式秩函数的次数可以将多项式秩函数分为线性秩函数和非线性多项式秩函数.

在线性秩函数研究方面,已有大量工作.譬如,2001年,Colón和Sipma通过凸多面体理论以及Farkas’ Lemma给出了一种计算线性秩函数的方法[12,13].2004年,Podelski和Rybalcheko提出了一种完备的方法来构造线性约束的单分支循环程序的线性秩函数[14].2012年,Bagnara等人[15]研究了线性程序的线性秩函数的计算复杂度问题.在2013年,他们提出了最终的线性秩函数(eventual ranking function)这一概念[16],并通过合成最终的线性秩函数来证明单分支线性约束循环程序的终止性.该方法首先利用一个单调增函数对循环程序的状态空间进行划分,然后利用Farkas’ Lemma来合成最终的秩函数.文献[17]将最终的线性秩函数进行了推广,提出了深度为L的最终线性秩函数.2014年,Leike等人针对线性循环程序,给出了包括多阶段秩函数在内的多个秩函数定义[18].2017年,Ben-Amram等人[19]对多阶段秩函数进行了进一步的研究,给出了一个能够在多项式时间内合成多阶段秩函数的方法.同时,他们还指出了多阶段秩函数和线性字典序秩函数(lexicographic linear ranking function)、嵌套秩函数(nested ranking function)之间的相互联系.相较于线性秩函数的研究,非线性多项式秩函数合成方面的工作较少,主要有以下几篇文献讨论了非线性多项式秩函数的计算.Chen等人[20]利用柱形代数分解(CAD)算法给出了一种合成非线性多项式秩函数的方法.该方法首先设定循环程序的非线性秩函数模板,然后将秩函数合成问题转化为半代数系统求解问题,从而可利用符号计算工具DISCOVERER和QEPCAD来求解半代数系统,最终得出非线性秩函数模板中参数的解.此外,文献[21,22]等人通过利用半正定规划 SDP工具来计算非线性多项式秩函数.

但程序的秩函数未必是多项式的.也即,可以构造一个循环程序,它并没有多项式秩函数但具有其他形式的秩函数[23].因此,当给定程序没有多项式秩函数时,我们还不能说它是不可终止的,因为它有可能有其他形式的秩函数.在本文中,我们主要研究下面给出的单重无条件分支的循环程序:

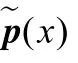
这里,p(x,z)=(p1(x,z),...,ps(x,z)),F(x,z)=(f1(x,z),...,fn(x,z)),且对任意的i∈[1,s],pi(x,z)∈Hn+1,di,对任意的j∈[1,n],fi(x,z)∈Hn+1,d.这里,对任意两个整数a,b且a≤b,记[a,b]={a,a+ 1,…,b-1,b},由文献[3,22]中的定理可知,程序与程序P在终止性上是等价的.

因此,不失一般性,本文主要分析下列齐次多项式循环程序终止性.

在下文中,我们将建立新的方法去探测程序Q的秩函数.该方法的主要思路是:将秩函数计算问题归结为二分类问题,然后利用机器学习中的支持向量机(SVM)算法[24,25]来合成所需秩函数,最终验证合成的秩函数是否满足秩函数定义.相较于当前的基于 CAD或 SDP的多项式秩函数计算方法,本文的主要贡献在于提出的基于SVM 的方法用于计算非多项式型秩函数——代数分式型秩函数,从而将秩函数的研究从多项式型秩函数扩展到代数分式型秩函数,扩大了可计算秩函数类型的范围.

本文第1节介绍秩函数、支持向量机等相关概念.第2节建立基于SVM的秩函数探测算法,并通过实例详细阐述该算法.第3节给出更多实验.第4节总结全文.

1 预备知识

1.1 秩函数

定义1.记号同上.给定齐次多项式循环程序Q.令ρ(x)为一个n元函数.ρ(x)被称为程序Q的秩函数,如果下列条件被满足:

则ρ(x)为程序Q的秩函数.

1.2 支持向量机

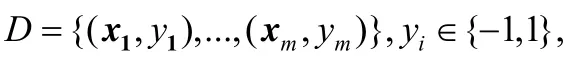
在样本空间中,划分超平面可用线性方程aTx+k=0来描述,其中,a=(a1,…,ad)是超平面的法向量,k是截距项.支持向量机可用于找到最“居中”的那一个超平面.如图1所示,支持向量机可以找到划分超平面aTx+k=0,该超平面将图中的两类样本点划分开,其中,落在aTx+k=1和aTx+k=-1上的点叫作支持向量.支持向量机的求解通常使用SMO算法[24]来实现.LIBSVM[25]是一个关于SVM的集成软件包,由台湾大学的Chih-Wei Hsu、Chih-Chung Chang以及Chih-Jen Lin编写完成.软件的主要部分采用C语言编写完成,可在MATLAB上调用.本文的主要计算部分即采用该软件包完成.

2 主要结果

本节阐述如何将型如程序Q的秩函数计算问题归结为二分类问题,以便可以利用支持向量机(SVM)工具来计算得到一个候选秩函数,最后再对该候选秩函数进行验证,以检验其是否满足秩函数的两个条件(a)和(c).

一般地,计算程序Q的秩函数,需要首先预设一个秩函数模板.秩函数模板形式可以是多种多样的.但为了方便计算,人们常将秩函数模板设定为多项式模板.但是,由于程序Q是齐次多项式程序,即其中的所有表达式都是齐次多项式的,因此下面的定理告诉我们,程序Q没有多项式秩函数.

定理2.记号同上.程序Q没有多项式秩函数.

这显然与式(3)矛盾.故程序Q没有多项式秩函数.

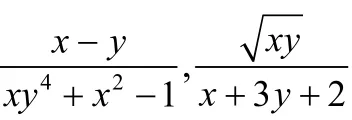
2.1 程序Q的秩函数计算归结为二分类问题

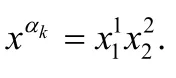
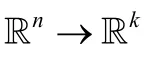
下面的命题表明,若T(x)在Ω上有定义,那么,函数T(x)为有界函数.也即,存在正数δ,使得对任意的x∈Ω有|T(x)|≤δ.

命题3.记号同上.若T(x)在Ω上有定义,那么,T(x)在Ω上有界.

证明:既然T(x)在Ω上有定义,则对Ω中任意一点x,T(x)中各个分量的分母均不会为0.考虑T(x)中第v段,即

这里,

显然有,

既然T(x),U(x)可被看作是ℝn→ℝk映射,若它们在Ω上有定义,则记

根据命题 3,若T(x)在Ω上有定义,那么T(Ω)是ℝk空间中的有界域.倘若存在某a∈ℝk,使得连续函数L(u)=aT⋅u在U(Ω)上有下界 1,即

那么,根据U(Ω)的定义有,

根据上述向量a,构造T(Ω)上的连续函数L′(t) =aT⋅t.既然T(Ω)有界,故L′(t)在T(Ω)上必有下确界,即存在c,使得∀t∈T(Ω) ⇒L′(t)=aT⋅t≥c.根据T(Ω)的定义,上式等价于

令ρ(x)=aT⋅T(x)-c.不难看出,上述式(6)对应于秩函数定义中的条件(c),式(7)对应于条件(a).因此,根据式(6)和式(7)以及秩函数定义,易知ρ(x)=aT⋅T(x)-c恰好是程序Q的秩函数,且是代数分式型的秩函数.从上述分析可以看出,若使得式(5)或者式(6)成立的向量a被找到,那么式(7)自然成立,从而可以构造得到程序Q的秩函数ρ(x)=aT⋅T(x)-c.因此,计算程序Q的秩函数,我们可以通过计算可满足式(5)或式(6)的向量a来得到.由此可得下列命题.

命题4.记号同上.若存在aT使得∀u∈U(Ω)⇒L(u)=aT⋅u≥1,那么程序Q有代数分式秩函数.要寻找使得式(5)成立的向量aT,我们可先对Ω的像集U(Ω)进行分析.

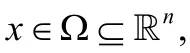
限制条件(C1)成立等价于O∉U(Ω ).

命题5.记号同上.假设U(x)在Ω上有定义.倘若ℝk空间中的原点O∉U(Ω),那么,计算使得式(5)成立的向量aT的问题就等价于:在空间ℝk中寻找可将原点O∈ℝk与像集U( Ω )∈ℝk严格分离的超平面.

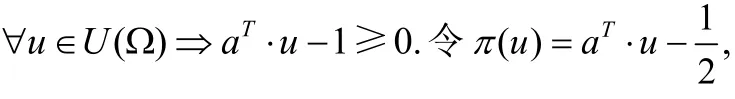
(i) ∀u∈U(Ω)⇒π(u)=aT⋅u+k＞0且π(O)＜0;

(ii) ∀u∈U(Ω)⇒π(u)=aT⋅u+k＜0且π(O)＞0.

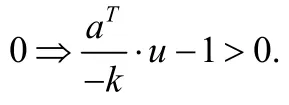
命题5将程序Q的秩函数计算问题与两个点集(单点集{O}与像集U(Ω)的隔离问题建立了等价关系.下面的情形(II)表明,即便原点O∉U(Ω),能严格分离单点集{O}与像集U(Ω)的超平面也未必存在.

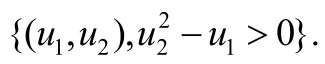
命题6.记号同上.U(Ω*)是ℝk中有界闭集.

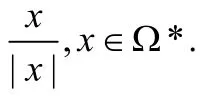
既然U(Ω*)=U(Ω*∩Θ),故有U(Ω*)是有界闭的.

如果O∉U(Ω*),根据命题6,既然U(Ω*)是有界闭集,那么在O与像集U(Ω*)之间存在间隙,因而有可能在二者之间存在严格分离超平面.既然U(Ω)⊆U(Ω*),当O∉U(Ω*)时,如果存在超平面π(u)能够严格分离原点O与像集U(Ω*),那么π(u)也能严格分离原点O与U(Ω).类似于命题5的证明,我们有下列结论.

定理7.记号同上.假设U(x)在Ω*上有定义且原点O∉U(Ω*)⊆ℝk.如果存在超平面π(u)可将原点O与像集U(Ω*)严格分离,那么一定存在向量aT使得式(5)成立.

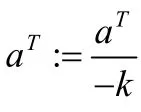
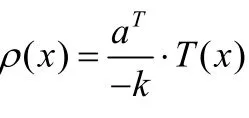
S1:从B集中取出有限个点记为B0⊆B.转S2;

S2:调用SVM算法计算单点集A与有限点集B0的分离超平面,记为π(u)=aT·u+k.转S3;

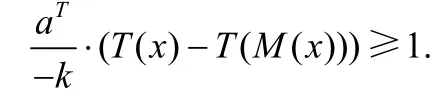
2.2 有限点集B0的构造

在上述的 S1中,需要从B=U(Ω*)中取出有限个点构成B0.由命题 8的证明可知,U(Ω*)=U(Ω*∩Θ).这里,Ω*∩Θ是一个有界闭集,Θ为单位球.因此,要构造B0,我们可以先从有界闭集Ω*∩Θ中取出有限点集C,然后通过U(x)映射得到点集U(C),从而得到B0=U(C).显然,直接在球面Θ上通过打格点的方式取点并不方便.但单位球Θ总是可以被包含在某个超立方体Δ中.故,为了构造Ω*∩Θ上的点集C,我们采取如下思路:先在区域Ω*∩Δ上构造点集S.这里,Δ=[-m,m]n为一超立方体.然后对点集S中的点进行归一化,得到归一化后的点集S0.显然,S0⊆Ω*∩Θ.最后令C:=So.而在超立方体Δ上打格子是相对容易的.因此,在区域Ω*∩Δ上构造点集S时我们可以通过对超立方体Δ打格子,然后将落入Ω*的格点收集起来构成点集S.图2所示为一个算法化的取点过程.

在上述算法中,需要设置m的值.在我们的实验中,m被取为100.此外,取点的间距h需要根据计算机的计算能力进行适当的调整,在计算机的实际计算能力范围内,间距越小,取得的样本点越多,最终计算出的代数分式函数经过验证成为真正秩函数的可信度就越高.

2.3 例 子

本节将通过一个例子来阐述上文提出的方法.

例1:考虑下列循环:

该循环若使用 RegularChains[26]或者redlog[27]来求解线性或者非线性秩函数,均会因复杂度太高,而无法在有效的时间内得出结论.接下来将演示如何通过上文提出的基于SVM的方法来探测循环程序P1的代数分式秩函数.

(a) 首先将循环程序Q1进行齐次化处理,变成终止性等价的循环程序Q1′,如下所示:

若式(8)无解,则表明O∉U(Ω*).由于代数分式以及根式的出现使得我们直接计算上述系统是否有解较为困难,因此,我们采取了一些化简措施.比如,将上述系统中的代数分式化为多项式,利用平方手段消除根号等.由此我们得到下列多项式系统:

显然,式(8)的任何一个解也必是式(9)的解.调用 Maple中的命令 solve计算可得式(9)仅有零解(0,0,0).显然,(0,0,0)∉Ω*.因为零解不可能是式(8)的解,故式(8)无解.这表明原点O∉U(Ω*).

综上所述,该循环程序满足定理7的前提条件.因此,根据定理7,秩函数计算问题可归结为O与U(Ω*)之间严格分离超平面的计算问题.

(b) 取样本点.

采用第 2.2节介绍的取点算法,并将该算法中的参数m=100.在本例中我们令取点间距h=1.由于在约束条件中有x3≥0的条件,故x3不必从-100开始取点.通过取点算法,我们得到U(Ω*)中的有限点集B0=U(C).将B0中的点的标签置为 1,而令单点集A=(O)的标签为-1.接下来调用 SVM 算法计算A与B0的严格分离超平面π0(u)=aT·u+k.

(c) 使用LIBSVM软件包计算出像空间中的划分超平面.

本文采用MATLAB调用LIBSVM软件包的方式来计算一个“硬分隔”的超平面.令=A∪B0.在求得划分超平面之后,需要对中的点进行一次完整的测试,测试结果必须是 100%完全精确才能进行下一步操作.对该例通过计算得到划分超平面中aT和k的值,

a=(2.798739925884132,-6.058645127373750,6.167554957795089),k=-1.000000000061875.

由上述计算得到的aT和k的值可确定一个严格分离超平面π0(u)=aT·u+k,它将A={O}与B0(⊆U(Ω*))严格分离.即:

(i) ∀u∈B⇒π0(u)=aT⋅u+k＞0且π0(O)＜0;

(ii) ∀u∈B⇒π0(u)=aT⋅u+k＜0且π0(O)＞0.

由类似于命题5的证明可知,无论哪种情形发生,都将有

接下来将验证超平面π0(u)是否能将A={O}与B=U(Ω*)严格分离.为此,就需要验证下列两种情形之一是否成立.

(i) ∀u∈U(Ω*)⇒π0(u)=aT⋅u+k＞0且π0(O)＜0;

(ii) ∀u∈U(Ω*)⇒π0(u)=aT⋅u+k＜0且π0(O)＞0.

既然像点u∈U(Ω*)且由U(Ω*)的定义可知U(Ω*)={u∈ℝk:u=U(x),x∈Ω*},那么验证上述(i),(ii)两式就等价于验证:

(i*) ∀x∈Ω*⇒β(x)=aT[T(x)-T(M(x))]+k＞0且k<0;

(ii*) ∀x∈Ω*⇒β(x)=aT[T(x)-T(M(x))]+k＜0且k>0.

这是因为,显然地,若(i)(或(ii))成立,那么(i*)(或(ii*))也必成立.反之亦然.

(e) 使用BOTTEMA软件包进行验证.

既然k=-1.000000000061875<0,那么我们需要验证:

是否成立.由于最终需要验证式(5)或式(6)是否成立,所以,在本例中,我们直接验证:

是否成立.BOTTEMA是一款强有力的不等式证明软件.它可以验证带复杂根式的代数表达式的不等式是否成立.我们可以在Maple上调用BOTTEMA中的各类函数.通过验证发现,

的确成立.故,

是该程序的代数分式型秩函数.因此循环程序是可终止的.

3 实 验

下面给出基于SVM的多项式循环程序秩函数探测的具体算法.

实验是在一台装有7.86GB的可用内存、处理器频率为2.59GHz、操作系统64位的Windows操作系统的计算机上进行的.下面我们选取了4个循环程序用于对比.每个循环程序具体的计算方法可以参照前文中的例1.

针对表1中的6个循环程序,我们先后用量词消去工具Redlog和Maple中的RegularChains软件包来计算各自的线性秩函数,从表2可以看出,除了循环程序P4和P5外,其他5个循环程序都不能通过量词消去方法来证明其是终止的.原因在于,量词消去算法的复杂度太高,当循环程序的赋值语句或循环条件中含有非线性项时,无法在有效的时间内给出计算结果.在表2中,unknown表示计算时间超过10个小时仍未得出结果.Terminating表示相应的线性秩函数或代数分式秩函数被成功找到,故表明循环是终止的.特别地,在Terminating后面的括号中给出了计算秩函数所花费的时间.显然,当循环中的表达式是线性时,基于量词消去的工具即能有效地计算它们的线性秩函数.但,当表达式中含有非线性项时,实验结果表明,量词消去工具较难在可接受的时间内计算线性秩函数.此外,本文提出的基于SVM的方法所涉及的时间开销包括:样本点集的构造所需时间、SVM计算时间以及用 BOTTEMA验证代数分式是否为秩函数所需时间.在实验中我们发现,本文方法最主要的时间开销在于样本点集的构造.譬如,循环P3,样本点集的构造花费了76分钟.当然,我们也可以尝试使用量词消去的方法来合成非线性秩函数,但是,非线性项的引入同样会带来高复杂度的问题.从表 2中可以看出,本文提出的基于SVM的秩函数探测方法能够探测出上述6个循环程序的确具有代数分式型秩函数,从而证明了这6个程序均是可终止的.上述6个循环程序在使用SVM的方法时,各自的取点间距h以及所产生的划分超平面aT·u+k中的参数aT和参数k的计算值见表3.

Table 1 More examples表1 更多实例

从表3可以看出,循环程序P3和P4所采用的取点间距为0.5,而循环程序P2采用的取点间距为0.2.从理论上来说,取点间距越小,所选取的样本点越多,最终计算出的代数分式函数被成功验证为秩函数的可能性就越大.但是考虑到计算机的实际计算能力,针对不同的循环程序,取点间距要作适当的调整.

Table 3 The parameters generated using the SVM method表3 使用SVM的方法所产生的参数

4 总 结

本文提出了一种基于支持向量机(SVM)理论的求解单重无条件分支多项式循环程序秩函数的方法.该方法将秩函数计算问题归结为二分类问题,然后利用SVM工具计算出一个候选的代数分式型函数,最后借助不等式自动验证工具BOTTEMA对其进行验证,以确定该代数分式型函数是否为循环程序的秩函数.由于SVM方法内部采用数值计算,因此相较于现有的基于量词消去的秩函数计算方法,本文方法能在可接受时间内探测形式较为复杂的秩函数.实验结果表明,针对某些循环程序,传统的量词消去方法不能在合理时间内判断出它们是否有线性秩函数,但通过本文提出的方法却可以找到其代数分式型秩函数.